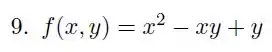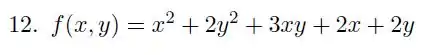Exercícios de Classificação de Pontos Críticos em Funções de 2 Variáveis - Lista de Exercícios Resolvida
Questão 3
A função possui
- Infinitos pontos de sela
- Infinitos pontos de máximo local
- Infinitos pontos de mínimo local
- Exatamente um ponto de mínimo local e um de máximo local
- Nenhuma das outras alternativas
Questão 4
Um fio de arame com de comprimento será cortado em 3 pedaços. Um deles será encurvado na forma de uma circunferêcia, outro na forma de um quadrado, e o terceiro na forma de um triângulo equilátero. Como deve ser cortado o fio para que a área combinada das três figuras seja a maior possível?
Ver solução completaQuestão 5
Seja em que e são números reais não nulos. Encontre os pontos críticos de e classifique-os em função de e .
Ver solução completaQuestão 6
Considere a função
O ponto
- É de máximo local
- É de mínimo global
- É de mínimo local
- É de sela
- Não é um ponto critico
Questão 7
Considere a função
o ponto
(a) é de mínimo local
(b) é de máximo local
(c) é de mínimo global
(d) é de sela
(e) não é ponto crítico
Ver solução completaQuestão 8
Em relação aos pontos críticos e da função , pode se dizer que:
(a) e são pontos de sela
(b) é ponto de máximo local e é ponto de mínimo local
(c) é ponto de sela e é ponto de mínimo local
(d) é ponto de sela e é ponto de máximo local
(e) nenhum dos outros itens
Ver solução completaQuestão 9
Seja em que e são números reais não nulos. Encontre os pontos críticos de e classifique-os em função de e .
Ver solução completaQuestão 10
1 - Determine e classifique os pontos críticos das funções abaixo relacionadas:
a) ;
Ver solução completaQuestão 11
Seja uma função com derivadas de segunda ordem contínuas tal que , e . Para qual das afirmativas abaixo, o ponto será um ponto de sela de ?
- Não sei
Questão 13
Encontre todos os pontos de máximos e mínimos locais e pontos de sela da função
Ver solução completaQuestão 14
Seja
Encontre e classifique (como pontos de máximo local, de mínimo local ou de sela) todos ao pontos críticos de .
Ver solução completaQuestão 15
A temperatura de uma placa quadrada de lado centrada na origem (e bordos paralelos aos eixos) é descrita pela função:
- Determine os pontos críticos de e classifique-os.
- Quais as temperaturas máxima e mínima da placa e onde elas ocorrem?
- Escolha um dos pontos críticos e dê a aproximação de no entorno deste ponto, escrevendo seu polinômio de Taylor de segunda ordem (grau 2)
- A partir do ponto em que direções a temperatura aumenta?
Questão 16
Seja dada por
- Determine os pontos críticos de
- Classifique os pontos obtidos no item anterior.
Questão 17
Considere as seguintes afirmações:
- Seja uma função diferenciável que possui um único ponto crítico. Se este ponto crítico é um entremante local de , então é extremante global de .
- Considere as e . Se as imagens de e estão contidas no gráfico de e é um ponto crítico de , então é um ponto de sela de .
- Se é um subconjunto não vazio e limitado de e é contínua, então é limitada em .
Assinale a alternativa correta:
- Somente a afirmação I é verdadeira
- Somente a afirmação II é verdadeira
- Somente a afirmação III é verdadeira
- Somente as afirmações I e II são verdadeiras
- Somente as afirmações II e III são verdadeiras
Questão 18
Seja
Onde são constantes reais. Assinale a alternativa cujos valores de fazem do ponto um ponto de sela de :
Questão 19
Seja
a) Determine os pontos críticos de e classifique-os.
b) Determine os pontos de máximo e de mínimo de sobre a região triangular de vértices e .
Ver solução completaQuestão 21
Seja
Seja
Com
- Encontre todos os pontos críticos de em .
-
• Encontre um aberto n, tal que restrita à seja estritamente côncava.
• Exiba um ponto
• Esboce .
- Exiba os pontos críticos de em que são pontos de máximo local, justificando sua resposta.
Seja
- Encontre funções , e tais que a função restrita ao aberto
Seja estritamente côncava. Exiba um ponto .
(Dica: use os calculos do item )
Ver solução completaQuestão 23
Sobre a função dada por
Considere as afirmações:
- Para todo , tem exatamente um ponto crítico
- Para todo , não tem pontos de mínimo local
- tem um único ponto de sela se, e somente se,
- Para é um maximo local de
São verdadeiras:
- Todas as afirmativas
- Apenas as afirmações II, III, IV
- Apenas as afirmações I e III
- Apenas as afirmações I, III, IV
- Apenas as afirmações III, IV
Questão 25
Questão 2: Considere a função .
- Determine os pontos críticos de .
- Classifique os pontos críticos de .
Questão 26
Seja
E seja definida por
- Seja o determinante da matriz hessiana de em . Obtenha as funções e tal que
- Classifique os pontos críticos de em
- Encontre funções e tal que restrita ao conjunto aberto
Seja estritamente convexa. Desenhe tracejando e explicite
Ver solução completaQuestão 27
Dada a função
- Determine seus pontos críticos.
- Classifique seus pontos críticos.
Questão 29
Seja
Onde são constantes reais. Assinale a alternativa cujos valores de fazem do ponto um ponto de máximo local de :
Questão 30
Seja
Resolva o que se pede:
- Determine os pontos críticos de .
- Classifique os pontos críticos de .
Questão 31
Seja
Onde são constantes reais. Assinale a alternativa cujos valores de fazem do ponto um ponto de mínimo local de :
Questão 32
Considere
- Determine conjunto aberto
- Esboce o conjunto aberto .
explicitando tal que restrita a seja estritamente convexa. Exiba a hessiana de e um ponto .
Questão 33
Determine se cada uma das seguintes afirmações é verdadeira ou falsa. Justifique sua resposta.
b) Se uma função com derivadas parciais de segunda ordem contínuas tal que . Se , então é um ponto de sela de .
Ver solução completaQuestão 34
Considere a função
- Encontre os pontos críticos de .
- Classifique os pontos críticos de quanto a sua natureza (máximo local, mínimo local ou sela).
Questão 35
Considere a função
onde e são duas constantes reais.
- Encontre os pontos (, ) tais que os autovalores da matriz hessiana de sejam estritamente positivos nestes pontos.
- Classifique os pontos críticos de quanto a sua natureza (máximo local, mínimo local ou sela).
Questão 37
3. Encontre os eventuais máximos locais, mínimos locais e pontos de sela da função
Ver solução completaQuestão 38
Seja
E considere as seguintes as afirmativas:
- possui exatamente três pontos críticos
- Apenas um ponto crítico de é ponto de mínimo local.
- Apenas um ponto crítico de é ponto de sela.
Indique a alternativa correta:
- Somente a afirmativa I é verdadeira
- As afirmativas I e II são verdadeiras e III é falsa
- As afirmativas I e III são verdadeiras e a II é falsa
- Todas as afirmativas são verdadeiras
- Todas as afirmativas são falsas
Questão 40
Sobre a função dada por
Considere as afirmações:
- Para todo , tem exatamente um ponto crítico
- Para todo , não tem pontos de mínimo local
- tem um único ponto de sela se, e somente se,
- Para é um paximo local de
São verdadeiras:
- Todas as afirmativas
- Apenas as afirmações II, III, IV
- Apenas as afirmações I e III
- Apenas as afirmações I, III, IV
- Apenas as afirmações III, IV
Questão 41
Seja uma função com derivadas de segunda ordem contínuas tal que . Suponha que seja um ponto de sela de , que e e que ; Qual das afirmativas abaixo é verdadeira?
- Nenhuma das demais alternativas.
Questão 42
Seja uma função diferenciável em . Considere a função . Então é correto afirmar que:
- Se e então não é possível concluir se possui valor extremo local em
- Se e então tem ponto de máximo em
- Se e então tem ponto de máximo em
- Se e então tem ponto de mínimo em
- Se e então tem ponto de mínimo em
Questão 43
(Capítulo 14.7 – Exercício 7) Determine os valores máximos e mínimos locais e pontos de sela da função.
Ver solução completaQuestão 44
(Capítulo 14.7 – Exercício 49) Determine as dimensões de uma caixa retangular de volume máximo tal que a soma dos comprimentos de suas 12 arestas seja uma constante c.
Ver solução completaQuestão 45
(Capítulo 14.7 – Exercício 10) Determine os valores máximos e mínimos locais e pontos de sela da função.
Ver solução completaQuestão 46
(Capítulo 14.7 – Exercício 11) Determine os valores máximos e mínimos locais e pontos de sela da função.
Ver solução completaQuestão 48
Determine os valores máximos e mínimos locais e pontos de sela da função
Ver solução completaQuestão 49
Seja , (.
- Calcule todos os pontos críticos de .
- Classifique os pontos críticos de , determinando se são máximos locais, mínimos locais ou pontos de sela.
Questão 50
Considere as seguintes afirmativas sobre a função
- é um ponto de sela
- é um ponto de mínimo local
- é um ponto de sela
- é um ponto de máximo local
- é um ponto sela
Assinale a alternativa correta:
- As afirmativas III e IV são as únicas corretas
- Ás afirmativas II e IV são as únicas corretas
- As afirmativas III, IV e V são as únicas corretas
- As afirmativas I e IV são as únicas corretas
- As afirmativas I e III são as únicas corretas
Questão 53
(Capítulo 14.7 – Exercício 53) Se o comprimento da diagonal de uma caixa retangular deve ser , qual é o maior volume possível?
Ver solução completaQuestão 54
Encontre os pontos e os valores mínimos e máximos locais e os pontos de sela (se houver) da função
Esboce o gráfico da função em torno dos pontos encontrados acima.
Observação: não é preciso esboçar o gráfico de toda função; apenas mostre como é o gráfico perto dos pontos de mínimo local, máximo local ou pontos de sela determinados.
Ver solução completaQuestão 55
Considere a função dada por
Onde é um número real não nulo.
- Para que valores de a função possui exatamente dois pontos críticos?
- Classifique os dois pontos críticos de obtidos no item anterior.
Questão 58
Seja , qual das afirmativas abaixo é verdadeira?
- possui somente um ponto crítico, e tal ponto crítico é um ponto de mínimo local.
- possui somente um ponto crítico, e tal ponto crítico é um ponto de sela.
- possui somente dois pontos críticos, sendo um de máximo local e outro de sela.
- possui somente um ponto crítico, e tal ponto crítico é um ponto de máximo local.
- Não sei
Questão 61
1 - Determine e classifique os pontos críticos das funções abaixo relacionadas:
b) ;
Ver solução completaQuestão 62
3 - Considere a função e a região .
(b) Encontre os máximos e mínimos de em .
Ver solução completaQuestão 63
A função possui
- Infinitos pontos de sela
- Infinitos pontos de máximo local
- Infinitos pontos de mínimo local
- Exatamente um ponto de mínimo local e um de máximo local
- Nenhuma das outras alternativas
Questão 64
Seja .
a) Encontre os pontos críticos de e classifique-os.
b) Existe que seja ponto de máximo ou de mínimo de em ? Justifique!
Ver solução completaQuestão 66
Seja
- Determine todos os pontos críticos de e os classifique
- Determine o máximo absoluto de no retângulo
Questão 69
2 - Encontre o máximo e mínimo globais de cada uma das seguintes funções:
b) , na região triangular com vértices , e ;
Ver solução completaQuestão 70
O ponto é um ponto crítico de cada uma das funções a seguir. Determine se esse ponto crítico é um ponto de máximo local, ponto de mínimo local ou um ponto de sela.
Questão 71
Q13. O polinômio característico da matriz
É . Temos que a solução do sistema de equações diferenciais satisfazendo a condição é dada por:
- ;
- ;
Questão 72
1 - Determine e classifique os pontos críticos das funções abaixo relacionadas:
c) ;
Ver solução completaQuestão 73
Dada a função
Determine e classifique os pontos críticos de em todo o
Ver solução completaQuestão 74
(2) Considere , definida em todo . Responda:
f) Classifique os pontos críticos (máximo ou mínimo local, ou ponto de sela).
Ver solução completaQuestão 76
Considere dada por . Assinale a afirmação verdadeira:
- possui exatamente um ponto de sela e três pontos de máximo local
- possui exatamente um ponto de sela e três pontos de mínimo local
- não possui pontos críticos
- possui exatamente um ponto mínimo local e três pontos de sela
- possui exatamente um ponto de máximo local e três pontos de sela
Questão 79
Uma empresa produz camisas e calças por mês. Cada camisa é vendida por e cada calça por . O custo total da empresta para produzir e vender camisas e calças é
Admitindo que tudo que a empresa produz é vendido de fato, determine a produção que maximiza o lucro da empresa, bem como o lucro máximo possível.
(Dica: o lucro é o total arrecadado com as vendas menos o custo de produção e venda).
Ver solução completaQuestão 80
Seja
Seja uma função definida em , onde
Com
- Classifique os pontos críticos de quanto a máximo local, mínimo local ou sela.
- Determine um aberto não vazio do plano (caso exista), tal que restrita à seja estritamente convexa (note que ). Depois desenhe .
Questão 81
- Determine se a função admite pontos de máximo/ mínimos, e caso sim, identifique-os .
Ver solução completaQuestão 82
Encontre e classifique todos os pontos críticos da função.
estabelecendo se são pontos de sela, pontos de mínimo local ou absoluto, pontos de máximo local ou absoluto. Justifique todos os detalhes!
Ver solução completaQuestão 84
Seja
- Determine todos os pontos críticos de e os classifique
- Determine o máximo absoluto de no retângulo
Questão 85
Uma determinada empresa produz dois produtos cujas quantidades são indicadas por e . Tais produtos são oferecidos ao mercado consumidor a preços unitários e , respectivamente, que dependem de e conforme equações: e . O custo total da empresa para produzir e vender quantidades e dos produtos é dado por . Admitindo que toda produção da empresa seja absorvida pelo mercado, determine a produção que maximiza o lucro. Qual o lucro máximo?
Ver solução completaQuestão 86
Uma indústria produz dois produtos denotados por A e B. O lucro da indústria pela venda de x unidades do produto A e y unidades do produto B é dado por:
Supondo que toda a produção da indústria seja vendida, determinar a produção que maximiza o lucro. Determine, também esse lucro.
Ver solução completaQuestão 87
Seja uma função com derivadas parciais de segunda ordem contínuas no ponto . Assuma que é um ponto crítico de e que , . Então é um ponto de mínimo local de se:
(a)
(b)
(c)
(d)
(e) a informação é insuficiente
Ver solução completaQuestão 89
Seja
Onde são números reais. Se
Então:
é ponto de mínimo local
é ponto de máximo local
não é ponto crítico
é ponto de sela
nenhuma das demais alternativas
Ver solução completaQuestão 90
Seja
Onde são constantes reais. Assinale a alternativa cujos valores de fazem do ponto um ponto de sela de :
Questão 91
Mostre que a função definida por admite máximo local em e mínimo locam em .
Ver solução completaQuestão 92
Considere as afirmativas sobre a função
- possui três pontos críticos distintos
- possui exatamente um ponto crítico e este é um ponto de mínimo local
- Há ao menos um ponto crítico de que é ponto de sela
- Todas as afirmações são verdadeiras
- As afirmações I e III são verdadeiras e a afirmação II é falsa
- As afirmações I e II são falsas e a afirmação III é verdadeira
- As afirmações I e III são falsas e a afirmação II é verdadeira
- As afirmações II e III são falsas e a afirmação I é verdadeira
Questão 93
Seja , onde . Então é ponto de máximo local de se?
não possui máximos locais;
;
;
.
Ver solução completaQuestão 94
Seja definida no quadrado aberto dado por e .
a) Calcule os pontos críticos de em
b) Classifique os pontos críticos de em
c) Determine um aberto na forma explicitando e satisfazendo as seguintes propriedades:
- A hessiana de em seja estritamente negativa definida.
d) Seja . Calcule o valor máximo e mínimo de restrita à .
Ver solução completa