Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 15
Utilize a integral dupla para determinar a área da região.
Um laço de rosácea .
Passo 1
Fala, galera! 😊
A questão pede para calcularmos a área de uma região usando uma integral dupla, no nosso caso, um laço de rosácea com
Mas que bomba é essa região? Se jogarmos essa informação acima no software, chegaremos a
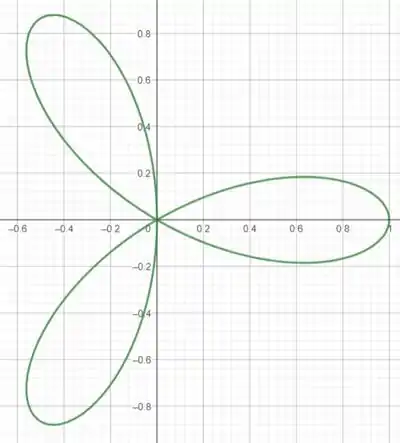
Sabemos que área de uma região é dada por
A melhor forma de trabalharmos com essa região é pelas coordenadas polares, já que a função da rosácea é mais fácil de calcular adaptando para esse sistema de coordenadas. Por isso:
Como estamos interessados na área total, vamos calcular um dos laços e depois multiplicar por , show?
Passo 2
Precisamos descobrir a região , ou seja, os limites de integração.
Para sabemos que
Mas em relação a , presta atenção!
Se fizermos
Mas se , como temos nos limites acima, então
Jogando o cosseno para o outro lado,
Ou seja,
E então, passando o pro outro lado, teremos
Assim, vamos nos restringir ao intervalo
Para um desses laços, temos
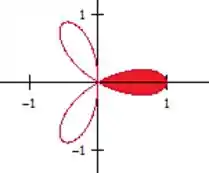
Passo 3
Montando nossa integral, chegaremos a
Fazendo a integral primeiro em :
Agora em relação a :
Como
Teremos
Show de bolinha! 😉