Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 18

Utilize a integral dupla para determinar a área da região.

A região dentro do círculo r = 1 + cos ⁡ θ e fora do círculo r = 3 cos ⁡ θ .

Passo 1

E aí, galerinha boa! Como vocês estão?

A questão pede para usarmos a integral dupla para acharmos a área da região:

dentro do círculo r = 1 + cos ⁡ θ

fora do círculo r = 3 cos ⁡ θ

Já vimos que essa integral será feita em coordenadas polares, já que os círculos estão em função de r e θ .

A integral dupla que nos dá a área de uma região em coordenas polares é:

A = ∬ D d A

Onde:

d A = r   d r   d θ

Então vamos precisar resolver a integral:

A = ∬ D r   d r   d θ

Passo 2

O próximo passo é determinar a região de interesse. Para isso, nada melhor do que desenhar o gráfico de r = 1 + cos ⁡ θ e r = 3 cos ⁡ θ em coordenadas polares. Veja:

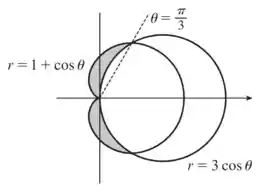
Observe que a região possui simetria acima e abaixo do eixo x . Dessa forma, basta nos preocupar em calcular a área acima do eixo x , e depois multiplicar a resposta por 2 .

Agora que já temos uma ideia da região, vamos calcular a intersecção entre elas. Para isso, devemos resolver a equação:

1 + cos ⁡ θ = 3 cos ⁡ θ

1 = 2 cos ⁡ θ

Ou seja,

cos ⁡ θ = 1 2 ⟹ θ = π 3

Observe que devemos dividir nossa área em duas regiões:

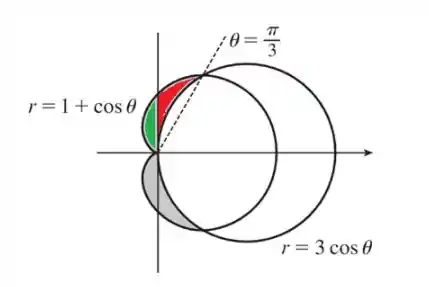
Fazemos essa divisão, pois na região vermelha, a área está entre r = 3 cos ⁡ θ e r = 1 + cos ⁡ θ e na região verde, a área está entre r = 1 + cos ⁡ θ e o eixo y . Dessa forma, nossa região D da integral é:

D = D 1 ∪ D 2

D = r ,   θ : π 3 ≤ θ ≤ π 2     e   3 cos ⁡ θ ≤ r ≤ 1 + cos ⁡ θ

∪ r , θ : π 2 ≤ θ ≤ π   e   0 ≤   r ≤ 1 + cos ⁡ θ

Passo 3

Dessa forma, temos que:

A = ∬ D r   d r   d θ = ∬ D 1 r   d r   d θ + ∬ D 2 r   d r   d θ

Vamos calcular cada uma dessas integrais, primeiro da região D 1 :

∬ D 1 r   d r   d θ = ∫ π 3 π 2 ∫ 3 cos ⁡ θ 1 + cos ⁡ θ r   d r   d θ = ∫ π 3 π 2 1 2 r 2 3 cos ⁡ θ 1 + cos ⁡ θ   d θ

∬ D 1 r   d r   d θ = 1 2 ∫ π 3 π 2 1 + cos ⁡ θ 2 - 3 cos ⁡ θ 2 d θ = 1 2 ∫ π 3 π 2 1 + 2 cos ⁡ θ - 8 cos 2 ⁡ θ   d θ

∬ D 1 r   d r   d θ = 1 2 ∫ π 3 π 2 d θ + 2 ∫ π 3 π 2 cos ⁡ θ d θ - 8 ∫ π 3 π 2 cos 2 ⁡ θ d θ

Lembrando que:

∫ cos 2 ⁡ θ = ∫ cos ⁡ 2 θ + 1 2 d θ = 1 2 1 2 sin ⁡ 2 θ + θ

Dessa forma,

∬ D 1 r   d r   d θ = 1 2 θ π 3 π 2 + 2 sin ⁡ θ π 3 π 2 - 8 ⋅ 1 2 1 2 sin ⁡ 2 θ + θ π 3 π 2 = 1 - π 4

Agora vamos pra segunda integral, a área da região D 2 :

∬ D 2 r   d r   d θ = ∫ π 2 π ∫ 0 3 cos ⁡ θ r   d r   d θ = ∫ π 2 π 1 2 r 2 0 1 + cos ⁡ θ   d θ

∬ D 2 r   d r   d θ = 1 2 �� π 2 π 1 + 2 cos ⁡ θ + cos 2 ⁡ θ d θ

Usando mesmo passo-a-passo que usamos anteriormente para calcular a integral acima, temos:

∬ D 2 r   d r   d θ = 3 π 8 - 1

Passo 4

Dessa forma, a área é:

A = 2 A 1 + A 2 = 2 1 - π 4 + 3 π 8 - 1 = π 4

Lembre-se que multiplicamos por 2 , pois as nossas integrais calcularam apenas as áreas acima do eixo x .

Resposta

π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}
Calcule a integral duplaint int_D (d x d y)/((p^2 + x^2 + y^2)^p) Onde: D = {(x , y) in R^2| x^2 + y^2 = a^2 } .
Se a0 , seja I a = ∫ - a a e - u 2 d u .Calcule as integrais sobre B 1 e B 2 , e use b ) para mostrar que I a tende para π quando a tende para + ∞ . Isto prova que ∫ 0 + ∞ e - u 2 d u = π 2 .