Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.1 - Ex. 23b
Vamos discutir, nesse problema, o erro de truncamento global associado ao método de Euler para o problema de valor inicial y′ = f(t, y), y(t0) = y0. Supondo que as funções f e fy são contínuas em uma região R fechada e limitada do plano ty que inclui o ponto (t0, y0), pode-se mostrar que existe uma constante L tal que |f(t, y) – f(t, ỹ |
Suponha que, se E0 = 0 e se |En| satisfaz a Eq. (i), então |En| ≤ βh²(α^n – 1)/(α − 1) para α ≠ 1. Use esse resultado para mostrar que. A Eq. (ii) fornece uma cota para |En| em termos de h, L, n e β. Note que, para um h fixo, essa cota aumenta quando n aumenta, ou seja, o erro aumenta com a distância ao ponto inicial t0
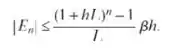
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nessa questão, vamos trabalhar com o erro associado ao truncamento das soluções do método de Euler. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser determinar o formato da solução com o truncamento local.
Ao substituirmos e agruparmos os termos, temos:
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!