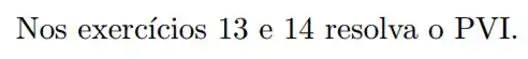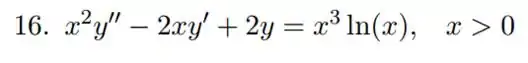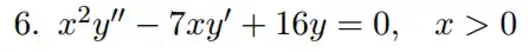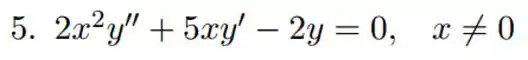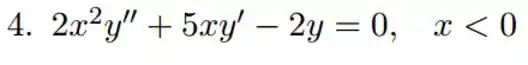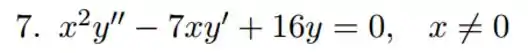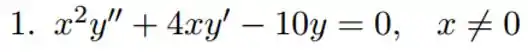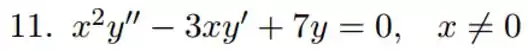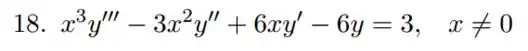Exercícios de Equação de Euler-Cauchy - Lista de Exercícios Resolvida

Encontre todos os valores de para os quais todas as soluções de tendem a zero quando .

Considere a seguinte família de equações de Euler:

Onde é uma constante real.

1. Encontre a solução da equação homogênea correspondente a que satisfaz as seguintes condições:

onde é a base do logaritmo neperiano.

2. Seja uma solução qualquer de com . Calcule o valor de .

Sugestão: encontre uma equação de Euler que seja satisfeita pela função .

Determine a solução geral da equação diferencial dada.

Considere a seguinte família de equações de Euler abaixo, onde é uma constante real.

1. Encontre a solução da equação homogênea correspondente que satisfaz as condições e , onde é a base do logaritmo neperiano.
2. Seja uma solução qualquer da EDO, com . Encontre o valor de .

Resolva PVI.

Resolva a equação de Euler

Seja e considerar a equação de Euler:

1. Determinar a solução geral de (2)
2. Determinar os valores de para os quais todas as suas respectivas soluções , encontradas em a), satisfazem a condição: .

Considere a seguinte família de equações de Euler abaixo, onde é uma constante real.

1. Encontre a solução da equação homogênea correspondente que satisfaz as condições e , onde é a base do logaritmo neperiano.
2. Seja uma solução qualquer da EDO, com . Encontre o valor de .

Considere a seguinte família de equações de Euler:

Onde é uma constante real.

1. Encontre a solução da equação homogênea correspondente a que satisfaz as seguintes condições:

onde é a base do logaritmo neperiano.

2. Seja uma solução qualquer de com . Calcule o valor de .

Sugestão: encontre uma equação de Euler que seja satisfeita pela função .

Questão 4 - Sabe-se que é uma solução da EDO no intervalo . Determine um conjunto fundamental de soluções para esta equação no intervalo .

Determine as raízes da equação indicial para a equação de Euler .

Escolha uma opção:

a) e

b) e

c) e

d) e

e) e

Encontre a solução do problema de valor inicial

Escolha uma opção:

a)

b

c)

d)

e)

f)

g)

h)

Seja a solução da EDO satisfazendo e . Então, é igual a:

Escolha uma opção:

a)

b)

c)

d)

e)

Encontre os valores de de modo que a solução do problema de valor inicial:

seja limitada quando .

Encontre de modo que a solução do problema de valor inicial

tende a zero quando tende a zero.

1. Encontre a solução geral da equação

No intervalo .

2. Seja uma solução da equação

Definida num intervalo . Fazendo , verifique que a função

Satisfaz uma equação diferencial linear de segunda ordem com coeficientes constantes.

Determine a solução da equação diferencial linear de 2ª Ordem não-homogênea com coeficientes lineares, tomando ,

Considere a equação de Euler com parâmetro

Encontre todos os valores de para os quais existe ao menos uma solução que satisfaz

Encontre todos os valores de para os quais todas as soluções de

tendem a zero quando tende a infinito.

Dada a Equação Diferencial Ordinária determine sua solução geral.

Resolva as equações diferenciais lineares não homogêneas com coeficientes constantes:

a)