Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 36

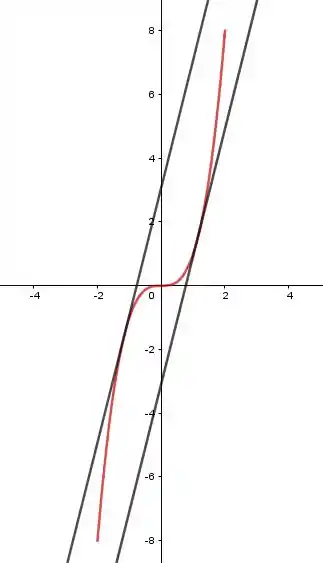
Verifique se as hipóteses do teorema do valor médio estão satisfeitas para a função dada no intervalo indicado. Então, ache um valor adequado de que satisfaça as conclusões do teorema do valor médio. Faça um esboço do gráfico de no intervalo e utilize-o para dar a interpretação geométrica desse teorema.

Passo 1

Como em é uma função polinomial, ela é continua derivável em qualquer intervalo de números reais. Em particular, é contínua em e derivável em .

Passo 2

Assim satisfaz as hipóteses do teorema do valor médio. Logo, existe tal que:

Pelas regras de derivação temos:

Assim, . Logo:

Passo 3

Assim, a reta que passa por tem inclinação e sua equação será:

E a reta que passa por tem inclinação e sua equação será:

Resposta

Portanto, o gráfico de no intervalo e da reta tangente a no ponto e , têm esboço:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Demonstre que a função apresenta valores extremos locais nos valores dados de θ e depois informe qual tipo de extremo local a função apresenta. h θ = 5s e n θ 2 , 0 ≤ θ ≤ π, θ = 0eθ = π

Esboce o gráfico de uma função derivável y = f ( x ) que passe pelo ponto (1,1) se f ' 1 = 0 e: f ' x0 para x f ' ( x ) 0 para x1; f ' ( x )0 para x f ' x 0 para x1 f ' x0 para x ≠ 1 f ' x0 para x ≠ 1

Esboce o gráfico de uma função derivável y = f ( x ) que tenha:um mínimo local em (1, 1) e um máximo local em (3, 3);um máximo local em ( 1,1) e um mínimo local em (3, 3); máximos locais em (1, 1) e (

Esboce o gráfico de uma função contínua y = g ( x ) tal que: g 2 = 2 , 0g '1 para x2 ,g ' x → 1 - quando x → 2 - ,- 1g '0eg ' x → - 1 + quando x → 2 + . g 2 = 2 ,g '0 para x2 ,g ' x → - ∞ quando x → 2

Esboce o gráfico de uma função contínua y = h ( x ) tal que: h 0 = 0 , - 2 ≤ h x ≤ 2 para todo x ,h ' x → ∞ quando x → 0 - , eh x → ∞ quando x → 0 + . h 0 = 0 , - 2 ≤ h x ≤ 0 para todo x ,h ' x → ∞ qu