Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 5e
Verifique as identidades.
onde é um natural
Passo 1
Fala, galera. Vamos resolver essa questão!
O enunciado pediu pra gente verificar a identidade:
onde é um natural.
Então, o que a gente tem que fazer é provar que essa igualdade é verdadeira. Repare que ela é uma expressão que pode ser resultado de uma divisão. Isso porque uma divisão na forma:
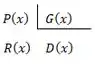
Onde é o dividendo, é o divisor, é o quociente e é o resto. Pode ser escrita como um produto na forma:
Então, vamos dividir por e verificar se o quociente e o resto da divisão nos permitem chegar na relação que o enunciado nos deu.
Vamos lá!
Passo 2
Montando a nossa divisão:
Para fazer essa conta, iniciamos dividindo o primeiro termo do dividendo, pelo primeiro termo do divisor, :
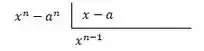
Agora pegamos o resultado, e multiplicamos por todo o divisor, . Daí, subtraímos do dividendo, . Fica assim:
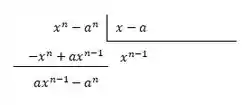
Mas a ideia aqui é chegar no menor grau possível! Então é só repetir esse processo com o resto, , até que o resto tenha grau menor que o divisor!
Passo 3
Repetindo o processo, teremos:
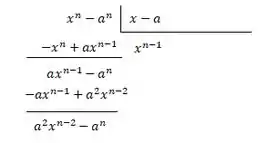
Dividindo novamente:
E mais uma vez:
Por fim, chegamos ao resultado da divisão com o resto zero:
Passo 4
Pronto, agora vamos transformar isso em uma expressão! Uma forma de escrever essa conta que fizemos é:
E pelas contas acima temos:
Dividendo
Quociente
Divisor
Resto
Assim ficamos com:
Como queríamos demonstrar.
Valeu, galera. Até a próxima! 😉