Verifique as identidades.x^5 - a^5 = (x - a) (x^4 + a x^3 + a^2 x^2 + a^3 x + a^4)

Enunciado

Para verificar a identidade primeiro vamos montar a divisão, lembre-se de como ela á composta:

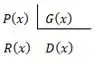
Onde é o dividendo, é o divisor, é o quociente e é o resto.

Vamos agora montar para o que querermos resolver:

Iniciamos dividindo o primeiro termo do dividendo pelo primeiro termo do divisor:

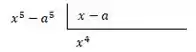
Agora pegamos o resultado e multiplicamos com todo o divisor, pegamos esse resultado, trocamos o sinal, e somamos com o dividendo, veja como fica:

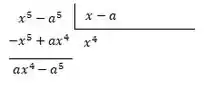
Pronto, agora é só repetir esse processo até que o resto tenha grau menor que o divisor, vamos lá:

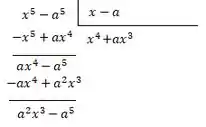
Novamente:

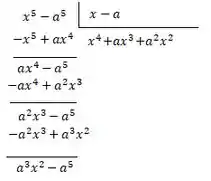
Mais uma vez:

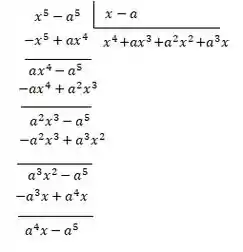
Fazendo mais uma última vez:

Pronto, agora vamos transformar isso em uma expressão, sabemos que:

E temos que:

Dividendo

Quociente

Divisor

Resto

Assim ficamos com:

Ei, a resposta está no passo a passo :)