Operações com Conjuntos
Teoria
Fala aí! Você chegou no Responde Aí! E vamos bater um papo sobre Operações com Conjuntos.
Quais São as Operações com Conjuntos?
Existem três operações básicas com conjuntos:
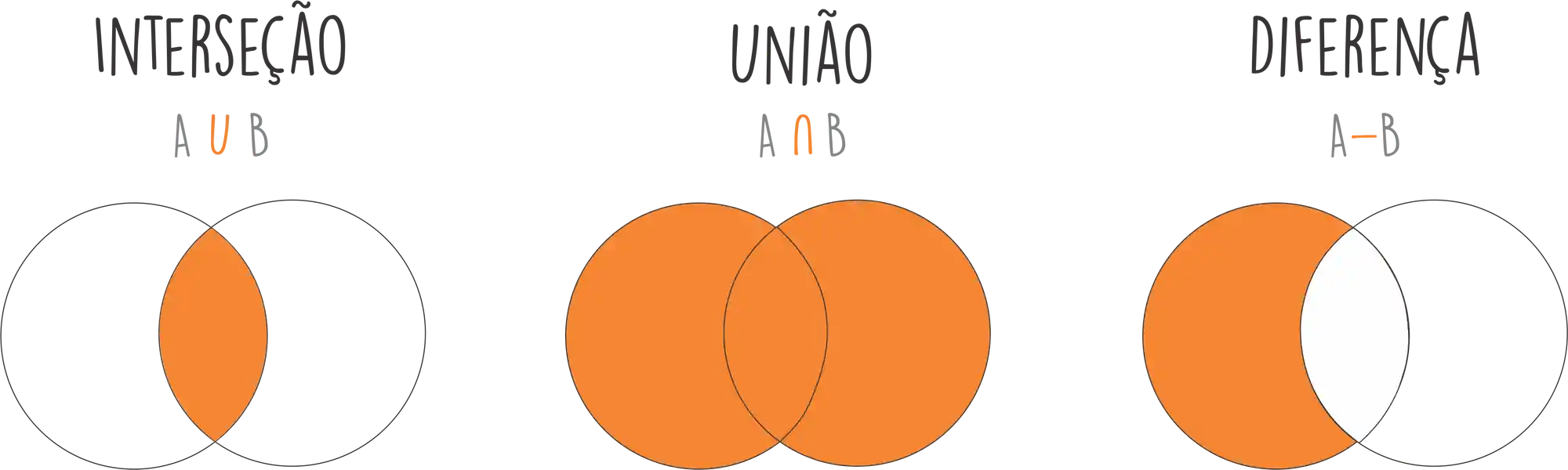
- Interseção: Nessa operação verificamos os elementos iguais nos dois conjuntos;
- União: Consiste em unir todos os elementos dos conjuntos;
- Diferença: Aqui, removemos os pontos de interseção.
Quando estivermos lidando com operações com conjuntos, vamos utilizar o Diagrama de Venn! Que é, nada mais nada menos, do que uma maneira de organizar os conjuntos utilizando circunferências!
Interseção de conjuntos
Na interseção de conjuntos olhamos os valores que aparecem, ao mesmo tempo, no conjunto
Por exemplo que eu tenho um conjunto
Agora imagina que eu quero um conjunto que tenha os números que são múltiplos de
Normalmente na construção de um conjunto, quando falamos de E, estamos falando de interseção. A notação é a seguinte:
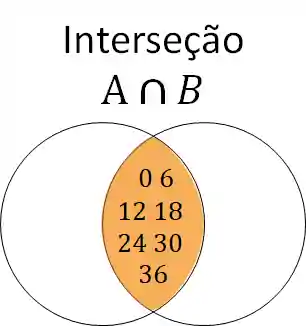
A região pintada representa o conjunto
📢 Clique para ver mais:
União de conjuntos
Para efetuar a união de conjuntos é só considerar todos os elementos existentes em
Vamos voltar nos conjuntos
A gente tem os conjuntos
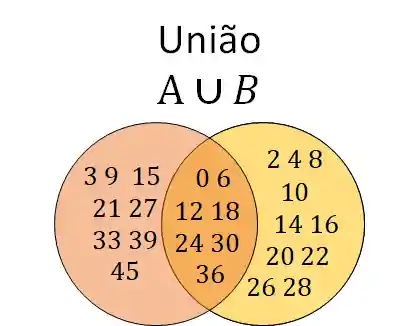
Tudo o que precisamos fazer é juntar os dois conjuntos! Normalmente na construção de um conjunto, quando falamos de OU, estamos falando de união.
Diferença de conjuntos
A diferença dos conjuntos é uma operação complementar à interseção!
Então é muito simples, por exemplo, se eu quiser um conjunto que tenha os múltiplos de
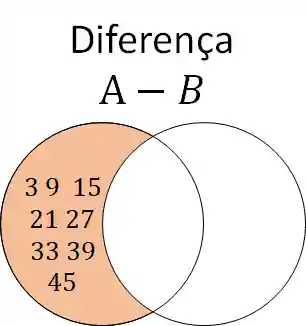
Normalmente na construção de conjuntos, quando temos RESTRIÇÃO, temos uma diferença de conjuntos. A diferença também pode ser escrita com uma barra:
E agora é hora de fazer uns exercícios 👇
União de conjuntos
Diferença de conjuntos
Exercícios Resolvidos
Exercício Resolvido #1
Sejam dados os conjuntos , e . Determine se são verdadeiras ou falsas as afirmações abaixo:
a)
b)
c)
d)
e)
Passo 1
Bom, vamos começar pelo item a). Então, dá uma olhada na seguinte afirmação:
Beleza, mas quem é ?
é um conjunto que possui como único elemento o número 0, ou seja, . Logo, queremos saber se .
Bom, em , temos o elemento dentro dele. Então, simmm:
Logo, o item a) é verdadeiro.
Uma observação: seria falso se fosse . Pois o elemento não está em , beleza?
Lembre-se: a nomenclatura “pertence” refere-se apenas a elementos.
Passo 2
Vamos agora para o item b):
Vamos lá: podemos dizer que se para cada elemento dentro do , esse elemento também está no . Ou seja, vamos olhar para cada elemento de e ver se ele também está em .
No caso, o único elemento de é o , certo?? E ele está em ?? Nãããoo! Como já até vimos na observação do passo anterior!
Quem está em é o elemento , não o , beleza??
Logo, a afirmação é falsa.
Lembre-se: a nomenclatura “está contido” refere-se apenas a conjuntos.
Passo 3
Show de bola! Vamos para o item c):
Essa afirmação está dizendo que existem elementos comuns nos conjuntos e , sendo assim a interseção desses dois conjuntos não gera um conjunto vazio.
SUPER MENTIRA!
Uma vez que não existem elementos comuns nos conjuntos e .
Não se confunde, hein!? possui o elemento 0, já possui um subconjuntos que tem como único elemento o número 0.
Passo 4
E o item d), é verdadeiro?
Bem, ele nos diz que existem elementos comuns nos conjuntos e , sendo assim a interseção desses dois conjuntos não gera um conjunto vazio.
VERDADE VERDADEIRA!
Já que os dois conjuntos possuem o elemento 0, logo o resultado desse interseção é um conjunto com um único elemento, que é 0.
Passo 5
Por fim, temos a afirmação e):
O conjunto está contido em ?
Vish! Super falso...
Isso porque precisaríamos que todo elemento de estivesse em também! E, de cara, isso não acontece, pois , mas não pertence a . Beleza??
Resposta
Portanto, temos aqui o nosso gabarito lindo:
a) V
b) F
c) F
d) V
e) F
Exercício Resolvido #2
Sejam x e y números tais que os conjuntos e são iguais. Então podemos afirmar que:
Passo 1
Cara, para dois conjuntos serem iguais, é necessário que eles tenham exatamente OS MESMOS elementos. Olha o nosso conjunto “incógnita” (vou chamar assim esse bonito):
O único elemento que ele tem em comum com o conjunto dado é o .
Então, a gente precisa que exista um e um ali no ou . Mas como a gente sabe quem é e quem é ? Seria e ? Ou talvez o contrário? Nunca saberemos hahaha
Passo 2
Vamos olhar pro conjunto dado:
E o nosso:
Lembrando que a ordem num conjunto não altera em nada os elementos. O conjunto é igual ao conjunto .
Beleza, acendeu uma luz aqui! Eu não posso afirmar nada, mas sei que a soma de todos os termos tem que ser igual, então:
Isso nos diz que:
E faz sentido né? Se você olhar pras opções, vai ver que elas não fazem sentido algum.
Passo 3
Começando pela letra
Isso é falso, pois se , os conjuntos não seriam iguais.
Isso também é falso, pois se , os conjuntos não seriam iguais.
Isso é falso, pois a relação correta foi a que encontramos.
Isso também é falso, pois suponha que , os conjuntos não seriam iguais!
Resposta
Exercício Resolvido #3
No diagrama de Venn-Euler abaixo, cada região foi denominada com um número entre parênteses indicar as regiões que determinam:
Passo 1
Amigx, se prepara porque você vai ver muito essa figura aqui no exercício hahaha BORA LÁ!
Vamos dar uma olhada no que ele pede:
Ou seja, a área comum do diagrama entre e , look at this:
Concorda comigo que é área de número ? É a parte que pertence tanto ao conjunto quanto ao , AO MESMO TEMPO.
Passo 2
Vamos dar uma olhada no que ele pede:
Ou seja, a área toda do diagrama que representa o conjunto e o unidos, take a look:
Concorda comigo que são as áreas de números ? São as partes que pertencem ao conjunto , ou ao ou aos dois.
Passo 3
Vamos dar uma olhada no que ele pede:
Ou seja, a área toda do diagrama que representa o conjunto e aí a gente tira tudo que é do conjunto também, take a look:
Concorda comigo que é a área de número ? É parte que pertence somente ao conjunto , sem nada do que tinha em comum com . Basicamente, é você tirar a interseção dos dois, que na figura era o número .
Passo 4
Vamos dar uma olhada no que ele pede:
Já que estamos tratando de complementar, vale dizer que o complementar de um conjunto é tudo aquilo que NÃO é o próprio conjunto. Na imagem, tenta ver quem seria o complementar de .
O que temos que pegar aqui são todas as áreas que NÃO são do conjunto , que no caso são as áreas de números e .
Passo 5
Vamos dar uma olhada no que ele pede:
Já que estamos tratando de complementar, vale dizer que o complementar de um conjunto é tudo aquilo que NÃO é o próprio conjunto. Na imagem, tenta ver quem seria o complementar de .
O que temos que pegar aqui são todas as áreas que NÃO são do conjunto , que no caso são as áreas de números e
Passo 6
Vamos dar uma olhada no que ele pede:
Agora que você já está cansado de ver o complementar, decidi dar uma esquentadinha. Bora tentar fazer esse? Faremos de duas formas. Primeiro, vamos resolver de dentro para fora, vamos ver quais são as áreas da união desses conjuntos:
São as áreas . Agora vamos tomar o complementar delas, ou seja, vamos pegar a área que NÃO seja ela, ok? Nesse caso é a área .
Agora faremos de outra forma, usando a propriedade do complementar:
Bom, já vimos que os números que representam o complementar de são e os números que representam o complementar de são .
O número que aparece nos dois é aquele que representa a área de interseção dos complementares. No caso, o número .
Passo 7
Vamos dar uma olhada no que ele pede:
Agora que você já está cansado de ver o complementar, decidi dar uma esquentadinha. Bora tentar fazer esse? Faremos de duas formas. Primeiro, vamos resolver de dentro para fora, vamos ver quais são as áreas da interseção desses conjuntos:
É a área . Agora vamos tomar o complementar dela, ou seja, vamos pegar a área que NÃO seja ela, ok? Nesse caso é a área representada pelos números .
Agora faremos de outra forma, usando a propriedade do complementar:
Bom, já vimos que os números que representam o complementar de são e os números que representam o complementar de são .
Se unirmos todos esses caras ficamos com .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Considere as seguintes afirmações sobre o conjunto :
Pode-se dizer que é(são) verdadeira(s):
Passo 1
Vamos começar analisando as proposições desde o começo:
Essa afirmação diz que:
Lembrando que é a quantidade de elementos que existem em .
Nesse ponto está correto pois tem realmente elementos.
Agora temos uma casca de banana, cuidado pra não pisar! Quando usamos o símbolo , estamos falando de um ELEMENTO pertencer ao conjunto.
O símbolo é o símbolo do conjunto vazio, que também pode ser substituído por . Perceba que ele não é um elemento do conjunto , logo, a afirmação é FALSA.
Passo 2
Essa afirmação diz que:
Lembrando que é a quantidade de elementos que existem em .
Nesse ponto está correto pois tem realmente elementos.
Quando usamos o símbolo , estamos falando de um conjunto ser um subconjunto de algum outro conjunto.
O símbolo é o símbolo do conjunto vazio, que também pode ser substituído por . Amigx, lembre-se de que o conjunto vazio é subconjunto de TODO conjunto! Logo, a afirmação é VERDADEIRA.
Passo 3
Essa afirmação diz que:
Note que realmente é um elemento de .
Além disso, é um subconjunto de , realmente. Pensa assim: ele é um conjunto pequenininho que tem um elemento que está em outro conjunto também!
Logo, essa afirmação é VERDADEIRA.
Passo 4
Dá uma olhada no que ela diz:
Isso é uma casca de bananaaaaaa! Fique atento! Dá muita vontade de dizer que está certo, né? Mas não está!!!
Quando fazemos a interseção entre dois conjuntos, o resultado é um CONJUNTO!!! O que temos ali é apenas um número, portanto, a afirmação é FALSA.
Resposta
Exercício Resolvido #5
Sejam conjuntos de números inteiros, tais que tem elementos, tem elementos, tem elementos e tem elementos. Então, o número máximo de elementos que o conjunto pode ter é igual a:
Passo 1
Bom, queremos né? Mas primeiro, vamos trabalhar com as informações que foram dadas:
Passo 2
Mas existe uma relação, que é a seguinte:
E olha só o que o problema nos forneceu! Vamos substituir:
Vamos guardar isso por enquanto, ok? Guarda aí!
Passo 3
Bora atacar o problema por outro lado:
Aqui vai mais uma relação:
Então:
Só que se a gente olhar para aquela equação ali:
Passando o termo pro outro lado, ficamos com:
Perceba que o lado esquerdo é justamente o que queremos, logo:
E como desejamos que ele seja MÁXIMO, isso só acontece quando e logo o número máximo de elementos é .