Conjuntos Numéricos
Produzido por Erick PinhoTeoria
FAAAAAALA AÍ!!! Amorzinho, agora que tu tá quase o próprio conjunto, eu vou te mostrar/relembrar alguns conjuntos muito tops que sempre aparecem e vão sempre aparecer em todos os seus cálculos: OS CONJUNTOS NUMÉRICOS!
Sem mais delongas, vamos a eles!
Conjunto dos Números Naturais
Cara, esse conjunto é o primeiro conjunto que você aprende na sua vida!!! Isso mesmo, você sem saber o aprende quando é uma criancinha, quando começa a contar os objetos e tal. Se liga:
O conjunto dos números Naturais é denotado por e se tu ainda não pegou qual a características dos elementos, eu te digo: são números maiores ou iguais a zero (chamamos isso de não-negativos) e são números inteiros!
Como isso aparece pra você? Você vai começar a ver conjuntos escritos dessa forma:
Daqui a pouquinho você verá que esses conjuntos são iguais! Segura aí hahaha
Só mais um comentário, há várias conversas sobre o pertencer ou não ao conjunto dos naturais.
Aqui consideraremos o como um elemento do conjunto, mas pergunte ao seu professor o que ele considera!
Conjunto dos Números Inteiros
Pois é, as coisas estavam indo muito bem, até que surgiram os números negativos!
“Pra que que isso surgiu?”
Cara, pensa assim: você imagina que tem 50 reais e quer comprar um livro de Cálculo que custa 120 reais... Quando vamos comprar alguma coisa, sempre pensamos com quanto dinheiro ficaremos, então fazemos a conta “o que tenho” “quanto vou gastar”.
Nesse caso, como que fica essa conta se o quanto você tem é menor do que quanto você irá gastar? Complicado, né? Então vamos criar números pra isso!!! Daí, temos o conjunto dos números inteiros:
Sacou? São “númeroZinteiros” hahaha Podem ser negativos, neutro ou positivos e você os verá tipo assim:
Perceba que , já que todos os elementos de pertencem ao conjunto
Conjunto dos Números Racionais
Show, agora esse cara chegou pra nos ajudar a fazer certas coisas! Por exemplo, eu gostaria de dividir meu sorvete com você, mas só tenho bola.
Eu gostaria que fosse impossível de dividir (daí eu ficaria com tudo hahaha), mas quando os racionais foram criados, essa divisão foi permitida.
A característica dos números que pertencem a esse conjunto é:
Então o conjunto pode ser escrito da seguinte forma:
Viu só a notação nova? *rycos*
Podemos juntar essas notações:
No geral, as frações são números racionais. Lembre-se de que dizima periódica é um número racional, pois podemos passa-la para o formato de fração. Exemplos:
O queeeee? Como assim é racional?!
Claro que é! Todo número inteiro é racional. Olha só:
A gente sempre pode escrever daquele jeito, então pronto!
Conjunto dos Números Irracionais
Agora essa! O que raios são os irracionais??? Cara, veja bem, o que vimos até agora foi que pra ser racional, é necessário que o número possa ser escrito na forma , onde e são inteiros e diferente de zero. Ok.
Aí eu te pergunto: E se a gente não puder escrever o número daquela forma? Quero dizer, deve existir algum número que a gente não consegue escrever desse jeito. E realmente existe! São os chamados números irracionais! Alguns exemplos:
No geral, dizimas não periódicas são números irracionais. Olha uns exemplos:
Perceba que esse número tem infinitas casas decimais e não tem um período nelas, então ele é irracional! A notação é ou I e você já vai ver quem é .
Conjunto dos Números Reais
Ooooooh! Finalmente chegamos ao último, mas não menos importante, conjunto numérico: Conjunto dos números reais!
“Ahn? Por algum acaso os que eu vi até agora não são reais?”
Hahahah são sim, esses aqui se chamam assim porque tem um outro conjunto que não veremos chamado de Conjunto dos números Complexos (que guarda os números imaginários, não reais), mas isso não vem ao caso!
O ponto é que o conjunto dos números reais é uma expansão dos racionais para guardar também os irracionais. Então a gente diz que o conjunto dos números reais é a união entre o conjunto dos racionais e o conjunto dos irracionais, saca só:
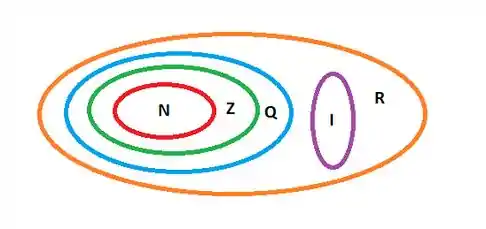
Perceba que os naturais estão contidos nos inteiros, que por sua vez estão contidos nos racionais!
Notações de Conjuntos
Bom, agora que já vimos esses conjuntos tops, vamos aprender a escrever bonitinho um conjunto. Existem duas formas (isso eu já falei): enumerativa e predicativa (famoso por extenso). Porém, quero falar aqui especialmente sobre um tipo que ainda não comentei: predicativa construtiva!
Ela é assim: consiste em apresentar os elementos de um conjunto através de expressões que envolvem variáveis. Na prática, ficamos com:
Exemplos:
Cara, você vai ter a expressão antes da barra e o que você faz é substituir os valores que pertencem ao conjunto dado. Este conjunto que fizemos agora é o conjunto dos números pares. Sabemos que para ser par, um número precisa ser múltiplo de , que matematicamente significa ser escrito na forma .
Um número para ser divisível por , precisa ser múltiplo do mesmo e, portanto, ser escrito da forma
Agora eu quero que você escreva o conjunto dos números ímpares!
“Como eu faço isso?”
GUARDA NO SEU SANGUE! Os números ímpares não são divisíveis por . E os ímpares podem sempre serem escritos como um número par somado a um número ímpar. Então façamos isso:
“Ah, mas por que você escolheu o ?”
Tudo bem, façamos de conta que eu escolho o :
Concorda comigo que eu posso escrever:
E se eu chamo:
A gente sempre cai no mesmo lugar. Então já sabe, número ímpar é daquele jeito ali!
Agora o seu professor quer que você escreva o conjunto dos números que quando divididos por deixa resto . Se liga, o processo é sempre o mesmo:
É isso por hoje, anjo! Bora exercitar!