Funções Trigonométricas – Parte 2
Produzido por Erick PinhoTeoria
Na primeira parte nós falamos sobre as principais funções trigonométricas: Seno e Cosseno.
Agora veremos as funções que utilizam essas duas, funções que dependem delas. Na prática, vamos usar muito do que vimos na Parte 1, fazendo algumas alterações, principalmente na parte gráfica.
A primeira função que veremos é a função tangente
Função Tangente
A função tangente é dada por
Bom, agora a coisa complica mais um pouco. Para achar o domínio dessa função temos que ver os pontos problemáticos, como temos uma divisão, serão os pontos onde o denominador é zero porque NÃO existe divisão por zero!!!
O denominador da função zera quando o zera e como essa é uma função periódica, a cada novo período temos mais pontos de que zeram a função:
Isso resulta em infinitos pontos de pra gente avaliar:
Mas repara que existe um padrão, começamos com e depois vamos somando ao ponto anterior. Podemos escrever uma fórmula geral pra isso, onde o representa números inteiros, que podem ser positivos ou negativos:
Então, o domínio da função tangente é o conjunto dos números reais, excluindo esses pontos problemáticos, que escrito formalmente fica:
Quanto à imagem, que é o que sai da função, nada limita a tangente, então a imagem é sempre o conjunto dos números reais:
E se quisermos a imagem de funções parecidas, como:
Ela também será igual ao conjunto dos números reais, assim como se multiplicássemos ou somássemos à função um valor qualquer.
Vimos então que existem alguns onde a nossa função não estará definida, isso também vai afetar como será formado o nosso gráfico. Novamente, vamos usar aquela tabelinha que tínhamos antes com os valores notáveis:
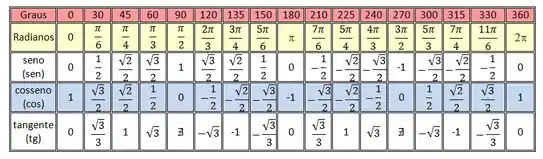
Observe que a função não está definida pros valores que mostramos antes e representamos isso na tabela com o símbolo . Mas se pegarmos valores nos aproximando cada vez mais desses pontos, a função vai aumentando cada vez mais.
Por exemplo, se fizermos na calculadora a tangente de 89,9°, que é beeem próximo de 90°, encontraremos:
E se aproximarmos ainda mais, temos:
E à medida que vamos nos aproximando mais e mais do temos valores cada vez mais altos e isso vai aparecer no nosso gráfico também, que vai tender pro infinito em alguns momentos. Desenhando ele, fica assim ó
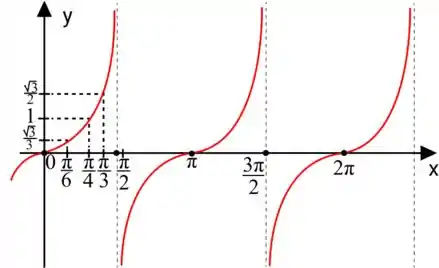
Uma observação: essas linhas verticais tracejadas representam aqueles pontos problemáticos onde a função não tá definida, a função pode se aproximar MUITO deles, mas nunca encosta de fato, já que não podemos calcular a função para esses valores de x.
Observe também que o período aqui é diferente do seno e do cosseno e vale .
Isso significa que se quisermos determinar o período de funções desse tipo
Teremos que igualar o argumento à :
Função Cotangente
A função cotangente é o inverso da função tangente, então podemos escrevê-la como
Além disso, como a tangente é dada por
A cotangente será o inverso, ou seja
Como são funções relacionadas, MUITO do que vimos pra tangente, vai valer também pra cotangente, por exemplo: para achar o domínio dessa função também temos que ver os pontos em que o denominador é zero já que NÃO existe divisão por zero!!! Só que aqui, ele vai zerar quando o zera, que acontece quando:
Assim como acontece com a tangente, temos infinitos pontos onde o denominador zera e vamos representar isso com uma formulinha:
Logo, o domínio da função cotangente é o conjunto dos números reais, excluindo esses pontos problemáticos, que escrito em matematiquês fica:
Quanto à imagem, nada limita a cotangente e, portanto, a imagem é sempre o conjunto dos números reais:
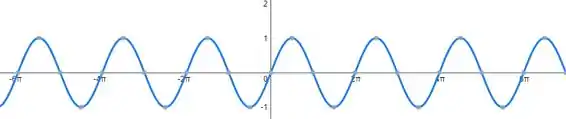
O gráfico dessa função fica muito parecido com o da função tangente, repara:
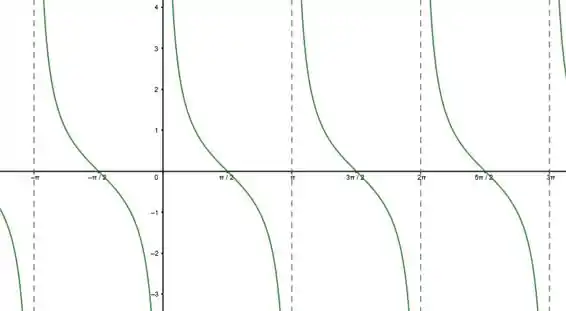
Só que aqui, a curva vai para o lado contrário e as linhas tracejadas que representam os pontos problemáticos correspondem aos zeros do e não do .
Função Secante e Cossecante
Chegamos nas últimas, eu prometo!
A função secante será dada por
Como temos o no denominador de novo, o domínio da função secante é o mesmo da função tangente, isto é
Quanto à imagem, temos o cosseno no denominador e no numerador o e para entender vamos começar com os pontos extremos do cosseno, que valem e , por exemplo:
A partir daí, quando o resultar em um valor entre e , a função assume valores maiores que , por exemplo:
E de forma parecida, quando o resultar em um valor entre e , a função assume valores menores que , por exemplo:
Dessa forma, a imagem da função estará sempre fora do intervalo e será:
Não foi erro de digitação, o colchete ao contrário indica valores fora do intervalo.
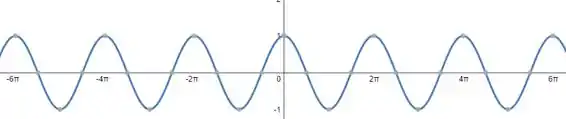
A secante, assim como o cosseno, terá período e o gráfico será:
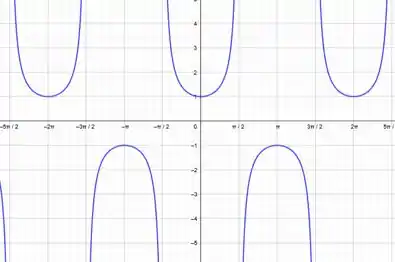
Já a cossecante será dada por
A cossecante será muuuito parecida com a secante, com apenas algumas diferenças!
A primeira é que como agora o seno está no denominador, precisaremos tirar do domínio os valores em que ele é igual a zero, e o domínio será igual ao da cotangente, que também tem seno no denominador:
Assim como acontece com o gráfico do seno e do cosseno que têm a mesma forma, mas estão deslocados, acontece com o gráfico da secante e cossecante. Então, o nosso gráfico fica assim ó
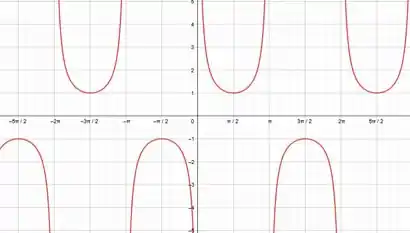
Pra você ver como eles são parecidos, olha eles lado a lado. O da secante está de azul e da cossecante, em vermelho.
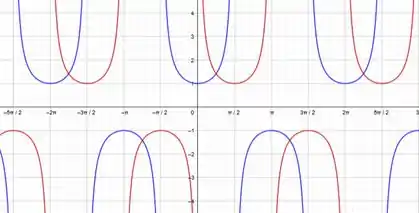
Show?
Agora, #PartiuExercícios
Função Cotangente
Função Secante e Cossecante
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
O período da função vale:
Passo 1
Falaaaaa Aí!! Como podemos encontrar o período dessa função???

Sabemos que o período da função cotangente é igual a , certo!?
Vamos partir daqui então!!
Passo 2
Para determinarmos o período, pegaremos o número que está acompanhando o
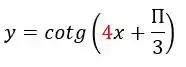
Que no nosso caso aqui será o número e faremos o seguinte
Agora, vamos isolar o para descobrir qual é o período da função . Assim,
Portanto, a nossa resposta é a letra C!!
Resposta
Letra C
Exercício Resolvido #2
Elaboração Própria
Na função seu período vale:
Passo 1
Vamos lá! Como podemos encontrar o período dessa função???

Sabemos que o período da função tangente é igual a , certo!?
Vamos partir daqui então!!
Passo 2
Para determinarmos o período, pegaremos o número que está acompanhando o
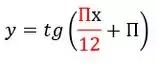
Que no nosso caso aqui será o e faremos o seguinte
Agora, vamos isolar o para descobrir qual é o período da função . Assim,
Portanto, a nossa resposta é a letra C!!
Resposta
Letra C
Exercício Resolvido #3
Elaboração Própria
Determine as imagens das funções abaixo:
Passo 1
Opaaaaa! Precisamos determinar a imagem de cada uma das funções, certo?!

Então vamos lá! Na letra (a) temos a função. Sabemos que a função está entre e :
Agora vamos multiplicar essa desigualdade toda por :
Assim,
Ou seja, a .
Passo 2
b) Na letra (b) temos a função .
Sabemos que a função deve estar entre e :
Certo? Como a nossa função é então vamos dividir toda a desigualdade por
Olha aíí!! Dessa forma, . Show de bola?!
Passo 3
Vamos seguir o mesmo raciocínio!! Sabemos que a função está entre e :
Agora vamos multiplicar a desigualdade por :
Assim,
Ou seja,

Passo 4
Pra fechar com chave de ouro, para a função da letra (d) vamos utilizar o mesmo raciocínio!!! Se
Então basta multiplicarmos toda a desigualdade por :
Assim,
Ou seja, .
Show de bola?!?!
Resposta
- .
Exercício Resolvido #4
Elaboração Própria
Verifique a identidade
Passo 1
Vamos lááá!! Queremos verificar que a igualdade é valida, beleza?!

Vamos partir de
E mostrar que conseguimos chegar em
Beleza?!
Passo 2
Se você reparar, temos o produto de uma soma e uma diferença! Podemos então utilizar os Produtos Notáveis! Não lembra??? Eu lembro pra você! Utilizaremos aqui
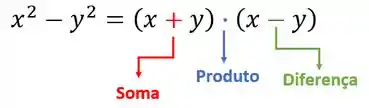
Assim,
Show de bola?!
Passo 3
EPAAAAAA! Se você reparar, temos uma identidade trigonométrica que diz que
Que é exatamente a expressão que encontramos após aplicar o Produto Notável!
Assim,
Beleza?!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
FEI-SP
O domínio, a imagem e o período da função
São, respectivamente:
- n.d.a
Passo 1
Fala Aííí!! Vamos lá!! A função tangente tem por definição o seguinte domínio:
Como podemos então encontrar o domínio da função
Já que é uma função tangente?!

É o que veremos agora!!!
Passo 2
Na desigualdade abaixo
No lugar de substituiremos pelo que temos dentro do parênteses da função tangente:
E resolveremos a desigualdade, isolando o !
Então vamos lá!!
Substituindo por
temos
Vamos olhar para
Jogando o para o lado direito da desigualdade, temos
Fazendo as contas
Assim,
Beleza... mas não temos essa opção!

Calmaa!!! Se você reparar no círculo trigonométrico
Assim,
O que rolou aqui?????? É que no resultado conseguimos estamos seguindo no sentido positivo (anti-horário) e na resposta ele está seguindo no sentido negativo do ciclo trigonométrico (sentido horário). Beleza?!
Para encontrar a imagem da função
Basta lembrarmos que toda função tangente tem umagem real e seu período é !
Logo, a nossa resposta é a letra (a)!
Resposta
Letra A
Exercício Resolvido #6
Elaboração Própria
Sobre a função representada no gráfico abaixo, quais das afirmações abaixo é a correta
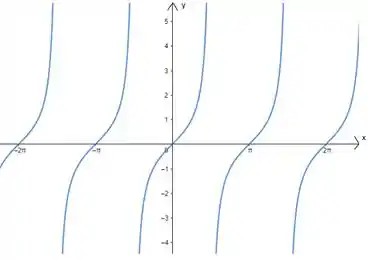
- A função do gráfico é a
- O período da função é
- O Imagem da função é
- O gráfico apresentado é da função
Passo 1
Fala Aííí!! Vamos analisar cada uma das afirmações para descobrir qual é a verdadeira?

Então vamos lá! Na letra (a) diz que a função so gráfico é a função . Vamos lembrar como é a carinha da função para compararmos?
A função tem essa carinha:
Passo 2
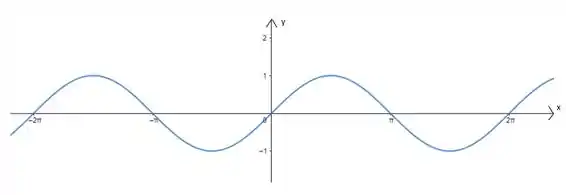
Que é bem diferente com o gráfico apresentado no enunciado, concorda? Rs. Então a letra (a) é falsa!!
Passo 3
b) Na letra (b) diz que o período da função é igual a . Vamos olhar para a imagem do gráfico novamente? Se você reparar na verdade o gráfico começa a se repetir num intervalo de tamanho
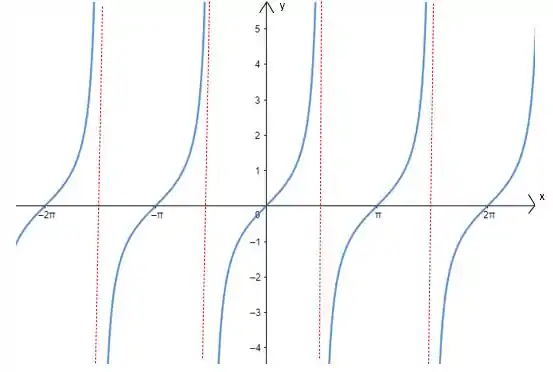
Ou seja, o período da função é e não . Assim, a letra (b) é falsa!
Passo 4
c) A letra (c) claramente vai ser falsa, pois a imagem da função é . Ela não se restringe como na função a :
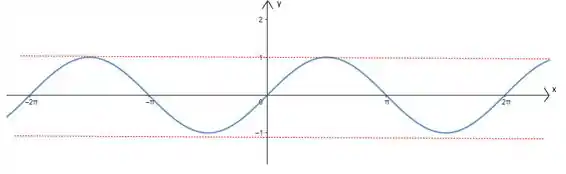
Passo 5
Assim, a opção que nos restou foi a letra (d)! E de fato, o gráfico apresentado no enunciado é o gráfico da função
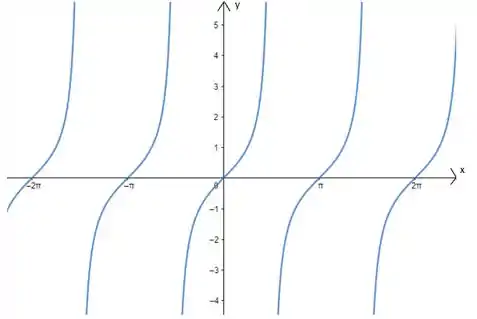
Onde seu domínio é
seu período e Imagem !
Beleza?!
Resposta
Letra D
Exercício Resolvido #7
Mackenzie 2017
Os valores de , para os quais a função não é definida, são
a)
b)
c)
d)
e)
Passo 1
Em outras palavras, o que queremos com esse enunciado é encontrar o domínio da nossa função.
Para uma função
Temos que o domínio é igual a
Passo 2
No enunciado, temos que
Para que essa função esteja definida, precisamos que o argumento dela, ou seja
Seja diferente de
Passo 3
Então teremos
Portanto, a resposta será a letra E.
Resposta
Letra E
Exercício Resolvido #8
IFCE 2016
Se e então o valor de é
a)
b)
c)
d)
e)
Passo 1
Beleza, a primeira coisa que vamos fazer, é dar uma simplificada naquela função. Temos
Como
Podemos escrever
Beleza, elevando aqueles caras ao quadrado, temos
Que será igual a
Até você deve estar pensando que não melhoramos muito em relação ao que tínhamos antes. Mas tem um pulo do gato, que será muito importante agora. Lembra daquela relação fundamental da trigonometria?
Ela diz que
Ou seja,
Então podemos escrever que
Beleza?
Divisão de Frações, nós repetimos o primeiro e....
Isso mesmo, multiplicamos pelo inverso do segundo. Portanto
Beleza, chegamos numa expressão bem mais amigável
Passo 2
No enunciado, temos a informação que. Então vamos utilizar isso agora
Novamente temos uma divisão de frações, então
Que será igual a
A resposta certa será a Letra A
Resposta
Letra A
Exercício Resolvido #9
Elaboração própria
Sendo determine o período e o domínio da função
Passo 1
Beleza, sabemos que o período da função cotangente é igual a
Para determinarmos o período, pegaremos aquele número que está ao lado do x, no nosso caso é o 2. Faremos o seguinte
Show?
Passo 2
O domínio da função cotangente é dado por
Mas como o que está dentro do nosso parênteses no exercício é o
Então teremos que
Ou seja,
Resposta
Exercício Resolvido #10
Epcar 2012
Considere o conjunto mais amplo possível na função real , dada por
Sobre a função é correto afirmar que
a)
b) é periódica com período igual a
c) é decrescente se
d) é ímpar.
Passo 1
Primeira coisa que vamos fazer, é procurar simplificar aquela função dada no enunciado. Temos:
Como e , podemos escrever
Que é igual a
Ou seja
Uma função bem mais amigável que aquela do início, certo?
Passo 2
Lembra da relação fundamental da trigonometria?
Ela diz que
Portanto, aquela função que tínhamos lá no início pode ser escrita como
Que é uma função CONSTANTE.
Sendo assim, ela não é nem periódica, nem decrescente e muito menos ímpar
Só vai nos restar a letra A como resposta, uma vez que ela será válida para o domínio dado.
Resposta
Letra A.