Função Modular
Produzido por Erick PinhoTeoria
Introdução
A função modular é uma função que transforma todo número dentro do módulo em um número positivo. Representamos da seguinte maneira:
Onde é o módulo de .
Podemos encarar o módulo como uma forma de calcular a distância de um número até o 0. Como não existe distância negativa, a ideia é sempre deixar o que tá lá dentro positivo, vamos ver uns exemplos antes de falar mais coisas complexas rs.
Vamos começar achando , isso é o módulo de , ou seja, temos que pegar o e deixar ele positivo, mas repara que ele já é positivo, então o módulo dele é ele mesmo:
Ou seja, a distância do 0 ao 2 é 2.
Agora vamos para , dessa vez o cara dentro do módulo é negativo, temos então que trocar o seu sinal para fazer com que ele fique positivo, assim seu módulo vai ser :
A distância do -3 ao 0 é 3
Repara naquele sinal de menos na frente ao tirar o módulo, é isso que faz o sinal ficar positivo no fim.
Entendeu a lógica? Sempre que o número for positivo, o seu módulo é ele mesmo, e sempre que um número for negativo nós vamos acrescentar um sinal de . Escrevendo isso matematicamente, temos:
Essa é a ideia da função modular!
Funções dentro do módulo
Uma outra forma de se usar a função modular é se tiver uma função dentro da outra, por exemplo:
Como vai ficar essa função? Vamos escrever a definição de módulo:
Repara que fizemos a mesma coisa de antes: trocamos pelo cara dentro do módulo. Mas isso não está nada arrumado ou fácil de entender. Temos que analisar aqueles intervalos da função. O que temos que fazer aqui é a análise de sinal desse cara dentro do módulo para saber quando ele é positivo e quando ele é negativo, e esses serão os intervalos da função.
Para a análise de sinal temos que fazer o esboço do gráfico dessa função, então vamos usar alguns conceitos da função quadrática. Primeiro, vamos usar Bhaskara para encontrar as raízes:
Além disso, como é positivo, a concavidade será para cima, temos então:
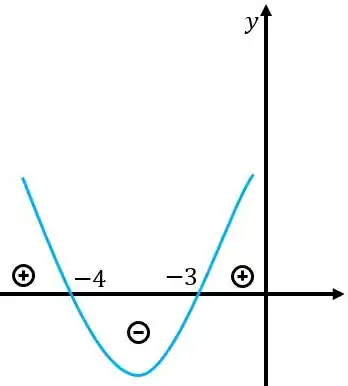
Assim vamos ter,
Assim, para aquela nossa função com módulo vamos mudar onde ele diz positivo e negativo pelos intervalos que achamos:
E pronto, agora temos a nossa função direitinho!
Gráfico envolvendo funções modulares
Aqui não é muito diferente do que fazíamos antes, quando temos uma função envolvendo coisas modulares.
A primeira coisa é separá-la pela definição:
Leva a:
Depois é só fazer o gráfico das partes. Vamos fazer a parte positiva, ou seja, em ou .
Isso é uma função de segundo grau, se fosse o intervalo completo, o gráfico seria:
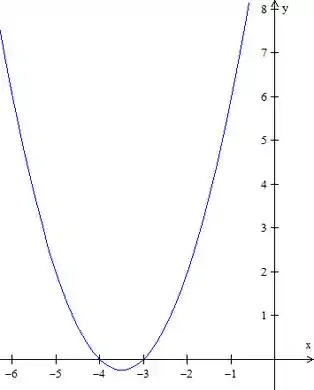
Mas aquela parte ali do meio, entre e não faz parte do intervalo, então temos que tirá-la:
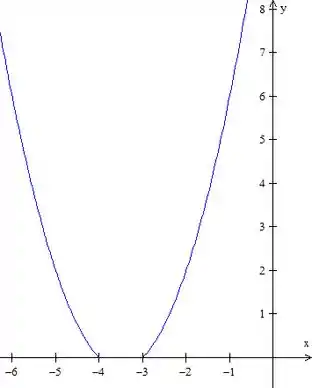
Falta aquele pedaço do meio, onde o gráfico é igual a esse azul só que com todo mundo de sinal trocado. Fazendo o gráfico inteiro, temos:
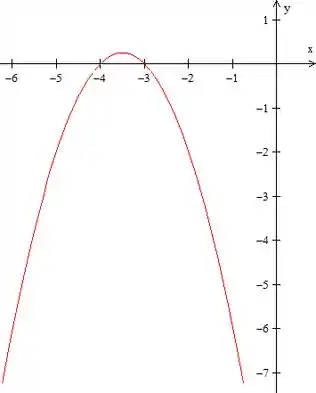
Mas só queremos aquela parte entre e , ficando:
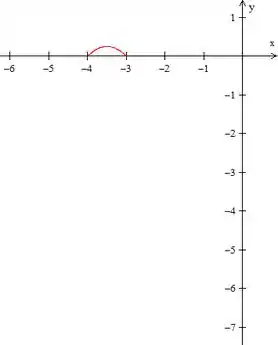
Juntando tudo, o gráfico vai ficar:
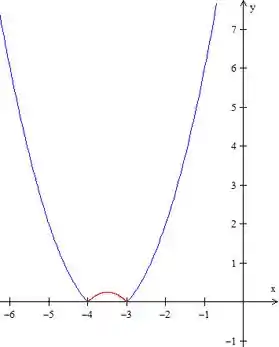
Uma forma mais simples de enxergar a construção do gráfico de uma função modular desse tipo é: primeiro construímos o gráfico da função ignorando o módulo, então identificamos as partes negativas da função e invertemos esses intervalos de baixo pra cima (marcado acima pela parte em vermelho).
Domínio e imagem
A presença do módulo não afeta o domínio da função, ou seja, o domínio de uma função polinomial, racional, exponencial ou logarítmica será o mesmo com ou sem módulo.
Já para a imagem, teremos mudanças. Como o módulo faz com que o valor seja sempre positivo, para a função mais geral , teremos:
Ou simplesmente:
Para não faltar nada...
A função modular é uma “fórmula” matemática que vai ajudar a evitar problemas em contas matemáticas, o exemplo mais clássico é quando temos a raiz de um número ao quadrado:
Normalmente você ia pensar, aaah é só “cortar” a raiz com o quadrado que vai dar . Olha, isso está errado, na verdade o resultado é o módulo de . Isso é para que o resultado de uma raiz quadrada seja sempre positivo, então fique ligado:
Sempre precisa desse módulo, se não a conta pode dar errado.
Funções dentro do módulo
Gráfico envolvendo funções modulares
Domínio e imagem
Para não faltar nada...
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine o domínio da função definida em por:
Passo 1
Bom, a primeira coisa que a questão diz pra gente é que a função é definida pelo conjunto dos números reais. Ou seja, os números imaginários estão fora, beleza?
Como a nossa função é uma raiz, o valor dentro dessa raiz tem que ser positivo pra que essa raiz seja um número real!
Por sorte a nossa função é uma função modular! Isso quer dizer que a o valor dentro do módulo vai ser sempre positivo, pois o módulo pega só o valor absoluto do que está dentro dele!
Então essa equação é maior ou igual a zero para todo logo, temos que
Resposta
Exercício Resolvido #2
Elaboração Própria
Construir o gráfico da função definida em por:
Passo 1
Bom para fazer o gráfico de uma função modular a primeira coisa que temos que fazer é fazer aqueles módulos pela definição, e depois vamos somar os pedaços das funções.
Assim
A outra parte vai ficar
Passo 2
Agora é só jogar isso de volta na fórmula da função para fazermos isso direitinho. Antes disso, vamos entender os intervalos que apareceram. Vamos ter partes, uma menor que , outra entre e e outra maior que .
A nossa função vai ser
Temos que ir vendo como é cada função daquelas do módulo nos intervalos, vamos olhar uma coisa de cada vez
Começando com , aqui vamos ter, olhando a definição de módulo
Vamos ter, para
Passo 3
agora com , aqui vamos ter, olhando a definição de módulo
Vamos ter, para o nosso intervalo
Passo 4
Vamos para , aqui vamos ter, olhando a definição de módulo
Vamos ter, para o nosso intervalo
Passo 5
Agora que vimos as partes, vamos escrever a nossa função
Temos funções de primeiro grau aqui, que são retas, então vamos pegar dois pontos em cada intervalo para fazer o gráfico,
Primeiro com
O gráfico dessa parte vai ficar
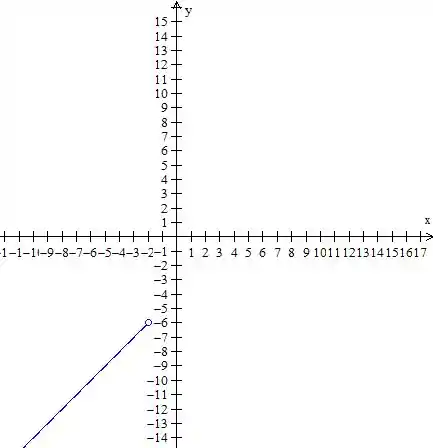
Lembra que temos que parar o gráfico em , mas o valor nesse ponto não entra na conta, por isso coloquei aquela bola aberta
Agora com
O gráfico dessa parte vai ficar
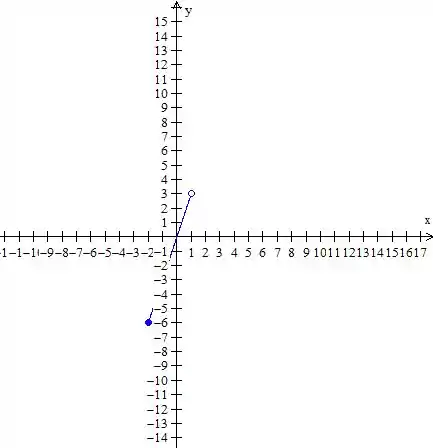
Lembrando que aqui temos que incluir o valor do extremo em , mas excluir a parte em
Para a última parte, onde , vamos ter
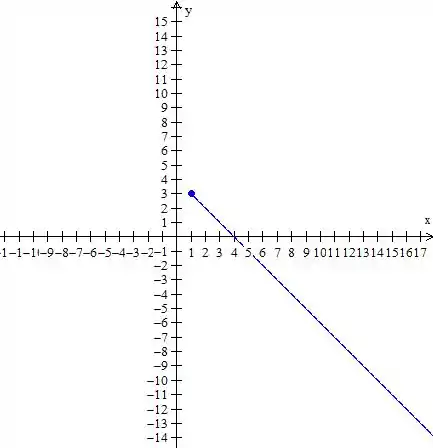
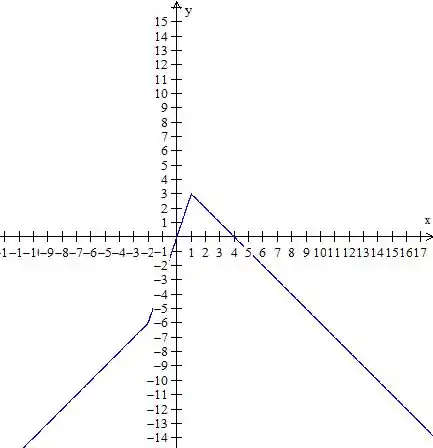
Agora é só desenhar tudo junto,
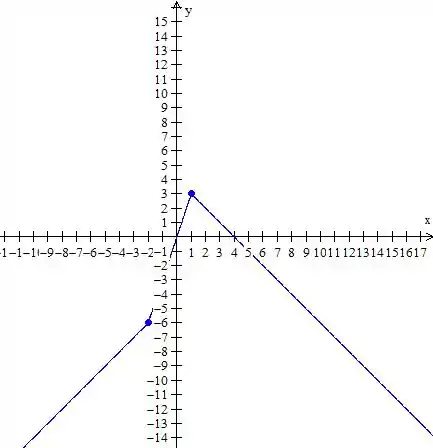
Essas “bolas fechadas”, como estão todas em cima da função mesmo, neste caso, não temos necessidade de deixar elas ali, se as funções não se juntassem nessa parte aí íamos precisar deixar, o gráfico fica
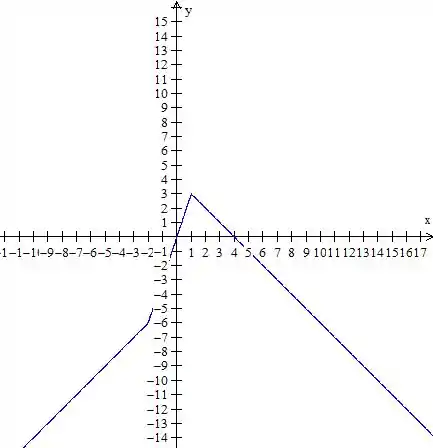
Resposta
Exercício Resolvido #3
PUC- RJ 2016
Seja
a) Para quais valores reais de x temos ?
b) Para quais valores reais de x temos ?
Passo 1
Lá vamos nós para a letra a), para resolvermos essa parada aí, vamos igualar a nossa função a 1. Daí, teremos o seguinte:
Ou seja,
Vamos resolver essas duas equações agora, a primeira vai ficar assim:
Agora, vamos para a segunda:
Tranquilinho, né?
Passo 2
#Partiu letra b) agora hein ...
Para descobrirmos onde a nossa função tem valores menores ou iguais a 1, vamos observar o gráfico dela.
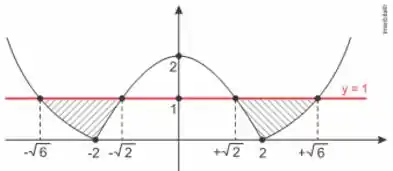
Perceba que a função tem y menor ou iguais a 1 para os seguintes valores:
Resposta
a) ou
b)
Exercício Resolvido #4
Elaboração Própria
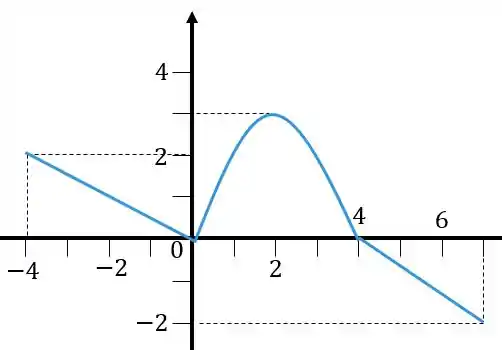
Dado o gráfico abaixo da função determine o gráfico de e
Passo 1
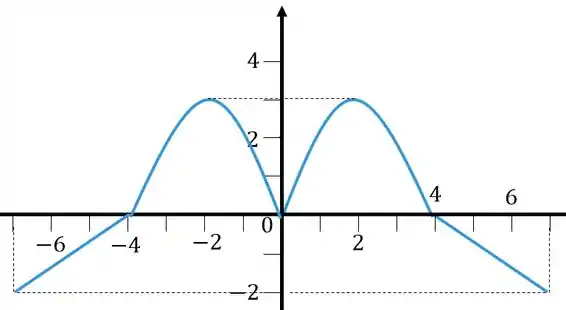
Vamos começar fazendo o gráfico de , lembra o que esse módulo vai fazer com a função? Ele sempre faz com que tenhamos no e quadrantes aquilo que está no e . Esse cara vai refletir ao longo do eixo , o gráfico vai ficar assim
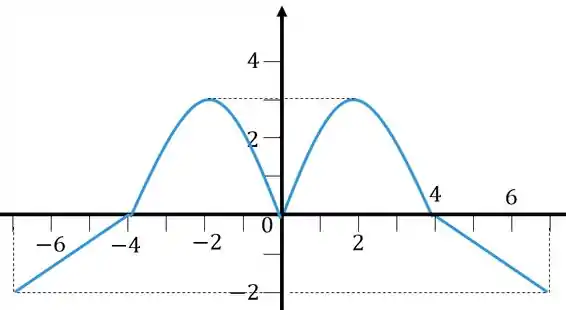
Passo 2
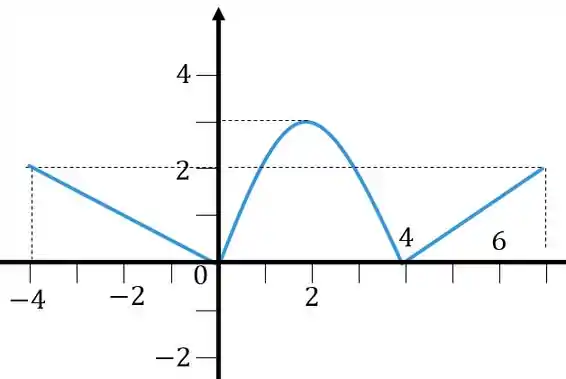
Como vai ficar a função ? Aqui o que for positivo, em , vai ficar positivo, o que for negativo, em , vai ficar positivo.
O gráfico vai ficar assim
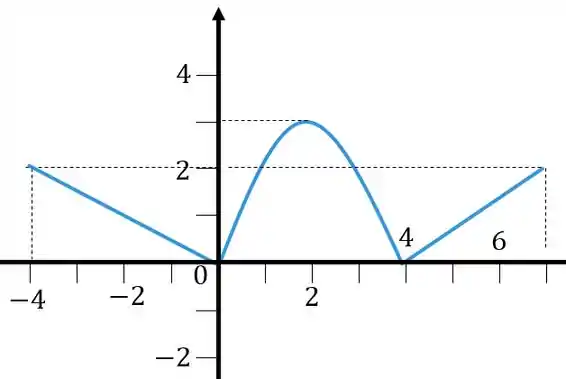
Resposta
Exercício Resolvido #5
Elaboração Própria
Dado o gráfico abaixo da função determine o gráfico de
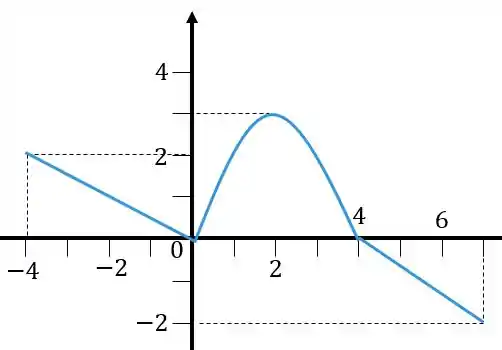
Passo 1
Eta que funçãozinha meio doida essa que ele quer o gráfico né?
Repara que temos varias transformações acontecendo ao mesmo tempo, para fazer o gráfico disso vamos fazer cada transformação em cima do gráfico anterior, ou seja, como diria jack o estripador vamos por partes.
Primeiro temos , como isso vai ficar? Lembra o que esse módulo vai fazer com a função? Ele sempre faz com que tenhamos no e quadrantes aquilo que está no e . Esse cara vai refletir ao longo do eixo , o gráfico vai ficar assim
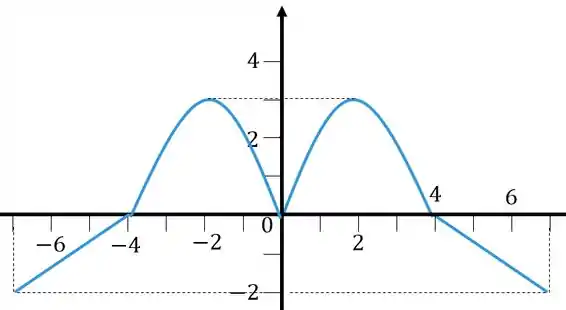
Passo 2
Ele somou a esse gráfico, esse está do lado de fora, então o gráfico vai subir unidade, ficando
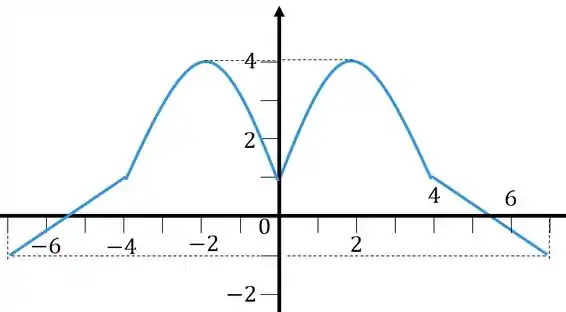
Passo 3
Agora temos um módulo de novo, esse módulo está por fora, aqui o que for positivo, em , vai ficar positivo, o que for negativo, em , vai ficar positivo.
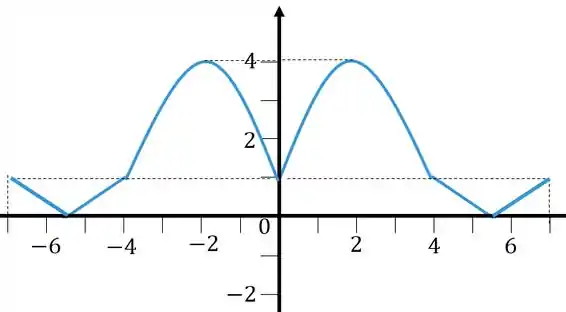
Passo 4
Agora temos esse sinal de menos, ele vai girar ao longo do eixo , o gráfico vai ficar
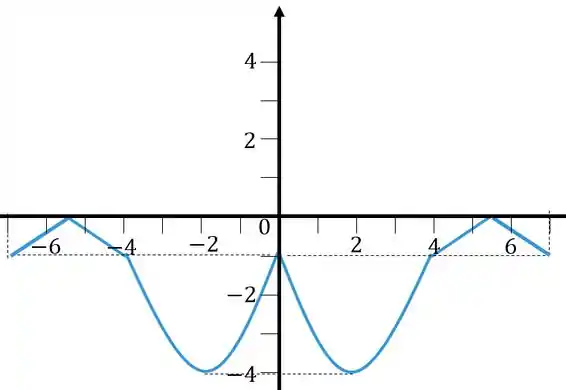
Passo 5
Agora ele quer subir unidades, resultando, finalmente, no gráfico de
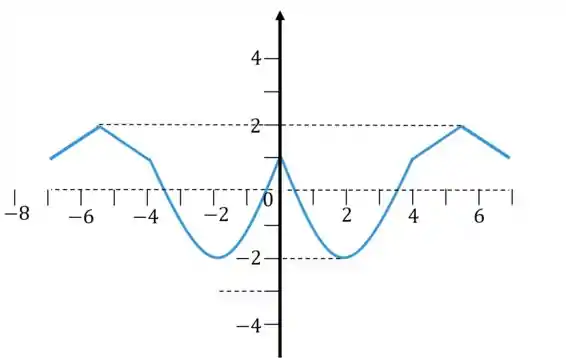
Resposta