Briot Ruffini - Divisão de Polinômios
Produzido por Erick PinhoTeoria
Fala aí, você caiu no Responde Aí! E vamos aprender a dividir polinômios usando o método de Briot-Ruffini
Os polinômios são aquelas expressões assim:
Show! Mas talvez você já tenha visto expressões assim:
Isso é uma divisão de polinômios. Para resolver isso, a primeira coisa que podemos fazer é tentar encontrar algum produto notável que simplifique a expressão de cima ou de baixo:
Show!
Mas o que acontece se aparecer algo assim:
Dessa vez, não dá para simplificarmos nada, teremos que realizar a divisão na mão mesmo, já sabemos que ela não será exata, ou seja, teremos resto.
Então, vamos lá descobrir como fazer isso
Divisão de polinômio por Briot-Ruffini
Olha só o exemplo que vamos resolver:
O que que gera isso ai? Po, é como divisão de número: gera um quociente e um resto. A gente pode escrever um polinômio
Caaaaaalma, que vou te explicar o que é cada um neste nosso caso!
Para fazer a divisão do exemplo, podemos usar Briot-Ruffini: Esse método é bem simples e vamos mostrá-lo para você passo-a-passo:
Passo 1: Armando o quadro
Primeiro, vamos traçar um quadro da seguinte maneira:

Na parte superior esquerda, colocamos o valor no qual o denominador zera, ou seja:

Na parte superior direita, colocamos os coeficientes do polinômio no numerador, não esquecendo dos zeros:
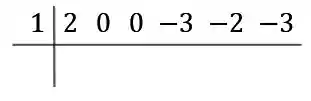
Passo 2: Multiplique e some
Repita o primeiro coeficiente da parte superior direita na parte de baixo:

E multiplique o número pelo coeficiente na parte superior esquerda:
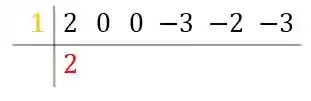
Some, então, o resultado com o coeficiente a direita e posicione o resultado logo abaixo deste:

Passo 3: Repita o passo anterior
Repita o processo até chegar ao termo que estará embaixo do seu último coeficiente. Esse será o resto da divisão:

Passo 4: Montando o polinômio
O último termo em lilás é o RESTO
A última coisa que falta agora é montar o resultado. Pegamos cada um dos coeficientes da parte inferior direita com exceção do lilás e montamos um polinômio com um grau a menos que aquele que dividimos.
Como aquele que dividimos tem grau
Prontinho!
Teorema do Resto
O teorema do resto é um teorema que permite achar o resto de uma divisão de polinômios sem nem mesmo dividir. É também uma excelente ferramenta para verificar o resultado da sua divisão. Em geral, o teorema é bem simples.
Se dividirmos um polinômio
Teremos que o resto será:
Que condiz com o resultado encontrado usando Briot-Ruffini.
Videoaula
Quer aprender ainda mais? Então confere essa nossa super videoaula
E aqui você tem um montão de exercícios pra praticar 👇
Divisão de polinômio por Briot-Ruffini
Teorema do Resto
Videoaula
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Qual o valor de que faz com que o resto da divisão de por seja ?
Passo 1
Vamos usar Briot-Ruffini para resolver essa questão. Queremos:
O denominador zera em . Vamos adicionar isso ao quadro:

Agora, marcamos os coeficientes na parte superior direita, lembrando que tem que entrar:
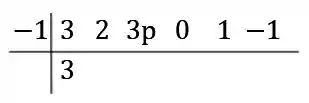
Passo 2
Agora, vamos multiplicar o primeiro coeficiente na parte inferior direita pelo na parte superior esquerda:
Somamos isso ao segundo coeficiente para parte superior direita:
Ficando:
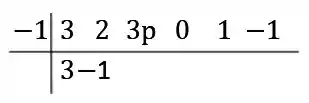
Fazendo agora aos demais:
Agora:
E:
Por fim:
Passo 3
Esse último resultado é justamente o resto, pois é o valor mais à direita no quadro do Briot-Ruffini. Queremos que esse resto seja , então igualamos:
Passo 4
Se utilizássemos o Teorema do Resto, teríamos que o resto da divisão de por , ou seja, por é igual a .
Vamos calcular dessa forma?
Como queremos que o resto seja igual a :
Resposta
Exercício Resolvido #2
Elaboração Própria
O polinômio tem divisão exata por ?
Passo 1
Olááá, jovem! Bom, para ter uma divisão exata, não podemos ter resto!
Eu poderia te dizer para usar o Briot-Ruffini (não estaria errado), mas eu sou muito sua amiga, então direi para você usar o Teorema do Resto!!!
Você lembra como ele é? Começa assim, temos uma divisão:
Para sabermos o resto dessa divisão, basta calcularmos .
Se esse resto for zero, significa que é uma divisão exata, ou ainda, significa que é uma raiz de .
Passo 2
No nosso caso, e
Então vamos calcular:
Logo, é raiz do polinômio, portanto o resto é .
Resposta
Sim.
Exercício Resolvido #3
Elaboração Própria
Determine o resto da divisão do polinômio:
Pelo polinômio:
Passo 1
OPAAA! Se ele quer saber simplesmente o resto, vamos usar o Teorema do Resto.
Dado que temos uma divisão do tipo:
O resto dessa divisão é dado por . No nosso caso:
Então, o resto será:
Resposta
O resto é .
Exercício Resolvido #4
Elaboração Própria
Uma das raízes do polinômio é 2. Pode-se afirmar que:
- As outras raízes não são reais.
- As outras raízes são 17 e -19
- As outras raízes são iguais
- As outras raízes estão entre -2 e 0
Passo 1
Temos que o polinômio será sempre divisível pelas suas raízes sem resto. Vamos fazer isso para simplificá-lo. Usamos Briot-Ruffini, chegamos ao quadro:
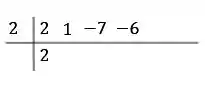
Completando-o:
Veja que o resto é zero conforme esperado. Podemos reescrever esse polinômio na forma:
Passo 2
As raízes do polinômio de segundo são as que faltam. Ele é mais fácil de resolver, podemos usar Bhaskara:
Assim, as raízes serão:
E:
Passo 3
Vamos ver qual alternativa se encaixa no resultado encontrado. Vemos que as raízes são reais, então a letra (a) está fora. Também não são nem e , então a (b) já era também. As raízes não são iguais, tiro fatal na (c).
Temos que . Junto de , vemos que as raízes estão entre e , logo a alternativa correta é a letra (d).
Resposta
Letra d.
Exercício Resolvido #5
Elaboração Própria
Efetue a divisão dos polinômios, encontrando o quociente e o resto.
Passo 1
Olá! Tudo bem?
Bom, nessa questão não temos muito pra onde correr. Vamos usar o Briot-Ruffini! Começamos montando a tabelinha:

Agora vamos posicionar os termos, lembrando que precisamos deixar todos os termos completinhos:
No nosso caso, já está tudo ok:
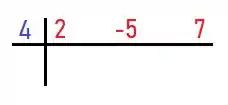
Passo 2
E agora realizar as operações: descer o primeiro coeficiente depois da barra

E multiplicar e assim, sucessivamente:
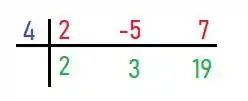
Passo 3
Perceba que o último termo é o nosso resto. E os números e são coeficientes do novo polinômio de primeiro grau:
Então: