Existência da Transformada de Laplace
Produzido por Carolina SabaTeoria
Introducão
Olá, galerinha! Para quem não lembra, a transformada de Laplace é a transformação de uma função dada por essa integral aqui:
Agora eu te desafio a fazer a transformada de Laplace da seguinte função,
Então pessoal, antes de você começar a tentar, eu tenho um recado para você: essa transformada não existe!
Opaaa, então você deve ta pensando, a transformada não vai existir sempre?
Na verdade, NÃO! Caso a função caia em umas dessas duas condições aqui embaixo, a transformada não vai existir:
- Se a função for de uma descontinuidade que você não consiga integrar, não tem como existir essa transformada.
- Outra forma de não haver a transformada é se a função for muito maior que a exponencial:
Então, voltando ao nosso desafio. Repara que a função possui uma descontinuidade em . Ou seja, a nossa não possui transformada de Laplace.
Mas e ai, como eu vou saber se uma função possui ou não transformada de Laplace? Então por isso que neste tópico nós vamos estudar a existência da transformada.
Existência da Transformada de Laplace
Bem, vimos duas condições nas quais a transformada não existe.
Mas, agora, eu te faço uma pergunta: será que toda função descontinua não vai possuir transformada de Laplace?!
Eita! Parece que to me contradizendo né?! Mas, então agora vamos ver as duas condições que contornam esses problemas de não existência da transformada de Laplace.
Função seccionalmente contínua
Olha o gráfico abaixo:
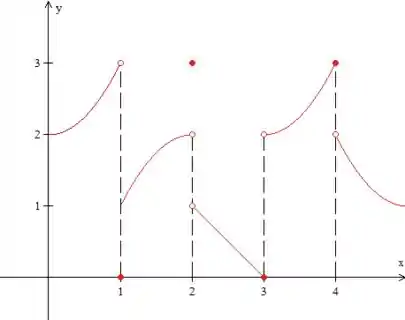
Repara que ele representa uma função que é contínua em um intervalo, exceto por um número finito de saltos. Ou seja, ela é contínua em partes, porém tem uns pontos de descontinuidade.
Então, a forma que posso contornar esse problema é: realizar a integração da função em subintervalos, assim a gente consegue calcular a transformada de Laplace dessa função.
Ordem exponencial
Vimos que o segundo problema acontece quando a função é muito maior que a exponencial. Neste caso, o que temos que fazer é garantir que a função não seja maior que a exponencial e sim menor! Quando você garante isso diz que ela é de Ordem Exponencial!
Por exemplo, olha a função abaixo e me diz como você que ela tem transformada?
Matematicamente, a gente quer garantir que isso aqui aconteça:
Para algum valor de e reais e no domínio da função .
Assim, devemos encontrar constantes e tais que:
Então vamos olhar para a nossa função. Lembra que a função cosseno é limitada:
E sabemos que a exponencial para no intervalo é sempre maior que (igual a se )
Ou seja...
Veja então que se tomarmos o e , por exemplo, já é o suficiente para falarmos que a função cosseno é de ordem exponencial! Ou seja, garantimos a existência dessa transformada.
Em resumo, essas condições são conhecidas como Condições de Existência da Transformada de Laplace:
- A função deve ser pelo menos seccionalmente contínua.
- A mesma função dever ser de Ordem Exponencial.
Agora vamos praticar!!!
Existência da Transformada de Laplace
Exercícios Resolvidos
Exercício Resolvido #1
Dennis Zill, Equações diferenciais volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2007, pp. 362-47. MODIFICADO
Mostre que a função do não possui transformada de Laplace.
Passo 1
Observando a função é perceptível que a função possui uma descontinuidade do tipo assíntota no ponto . Desta maneira, não existe transformada de Laplace, já que das condições para tal não são seguidas.
De outra maneira, podemos mostrar que a integral usada para calcular a transformada de Laplace diverge.
Vamos separar o intervalo para analisar melhor a parte próxima de :
Para a integral à esquerda. Se :
Que diverge. Se :
Logo, pela propriedade de comparação de integrais, divergirá. Para
Que divergirá também. Então essa transformada não existe.
Resposta
Ei, a resposta está no passo a passo :)