Função Degrau
Produzido por Carolina SabaTeoria
A função degrau unitário, também é conhecida como Função de Heaviside e ela é muito importante pra modelar fenômenos descontínuos! Ela tem essa carinha aqui 👇👇👇
Imagina calcular a transformada de uma função que possui saltos?! Por isso a gente precisa entender bem o que é a função degrau e como representa-la! Bora lá?
📢 Clique para ver mais:
- Função Degrau Unitário: Exercícios Resolvidos
- Transformada de Laplace da Função Degrau
- Tabela Transformada de Laplace
O que é uma Função Degrau?
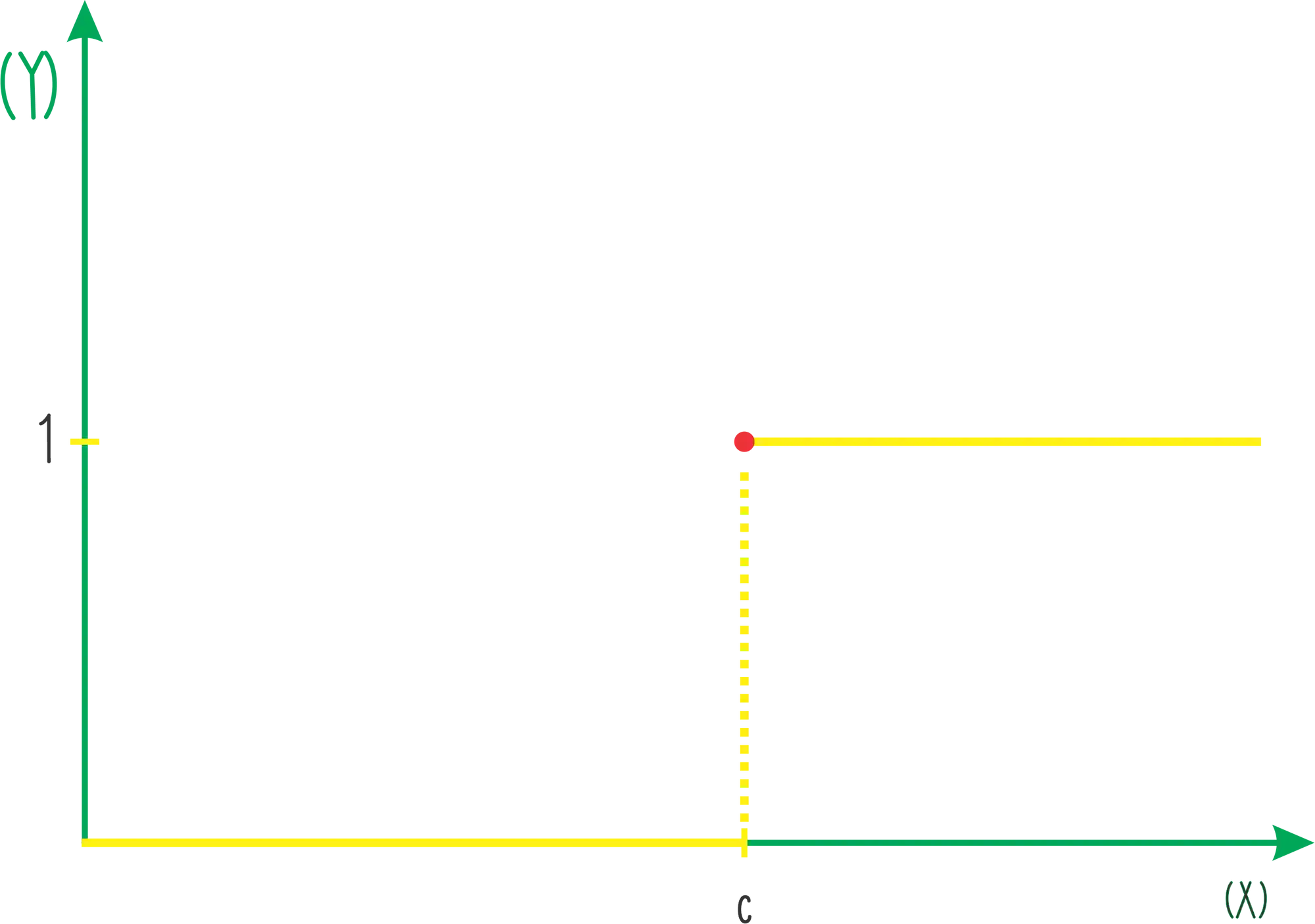
A função degrau tem esse nome porque ela parece um degrau de uma escadinha mesmo! Podemos escrever a função acima da seguinte forma:
Ou seja, quando
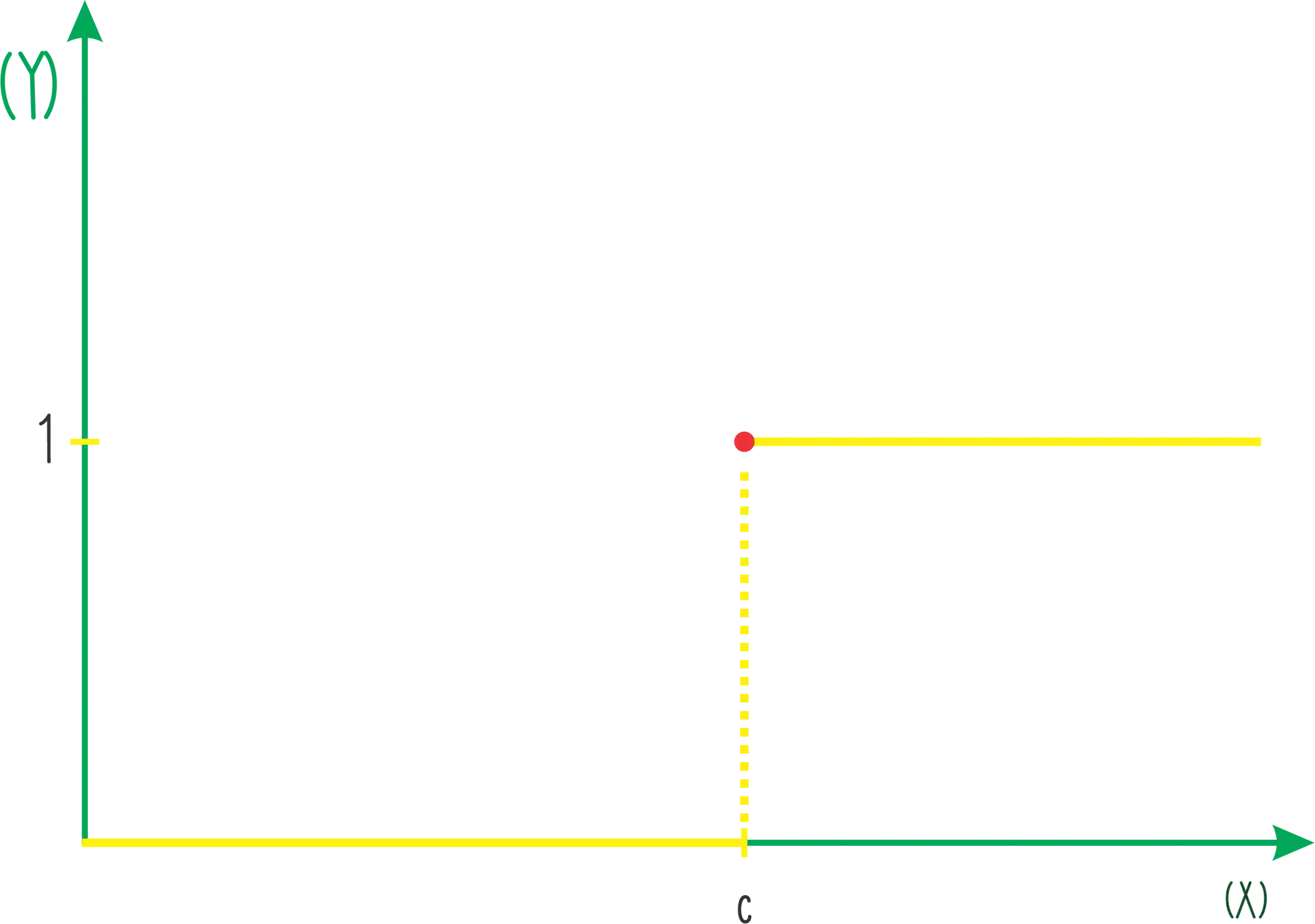
Como essa não é uma função qualquer e sim uma função muito importante, ela tem uma notação própria: é denotada por , então fica assim
O que estamos dizendo ai em cima é que a função
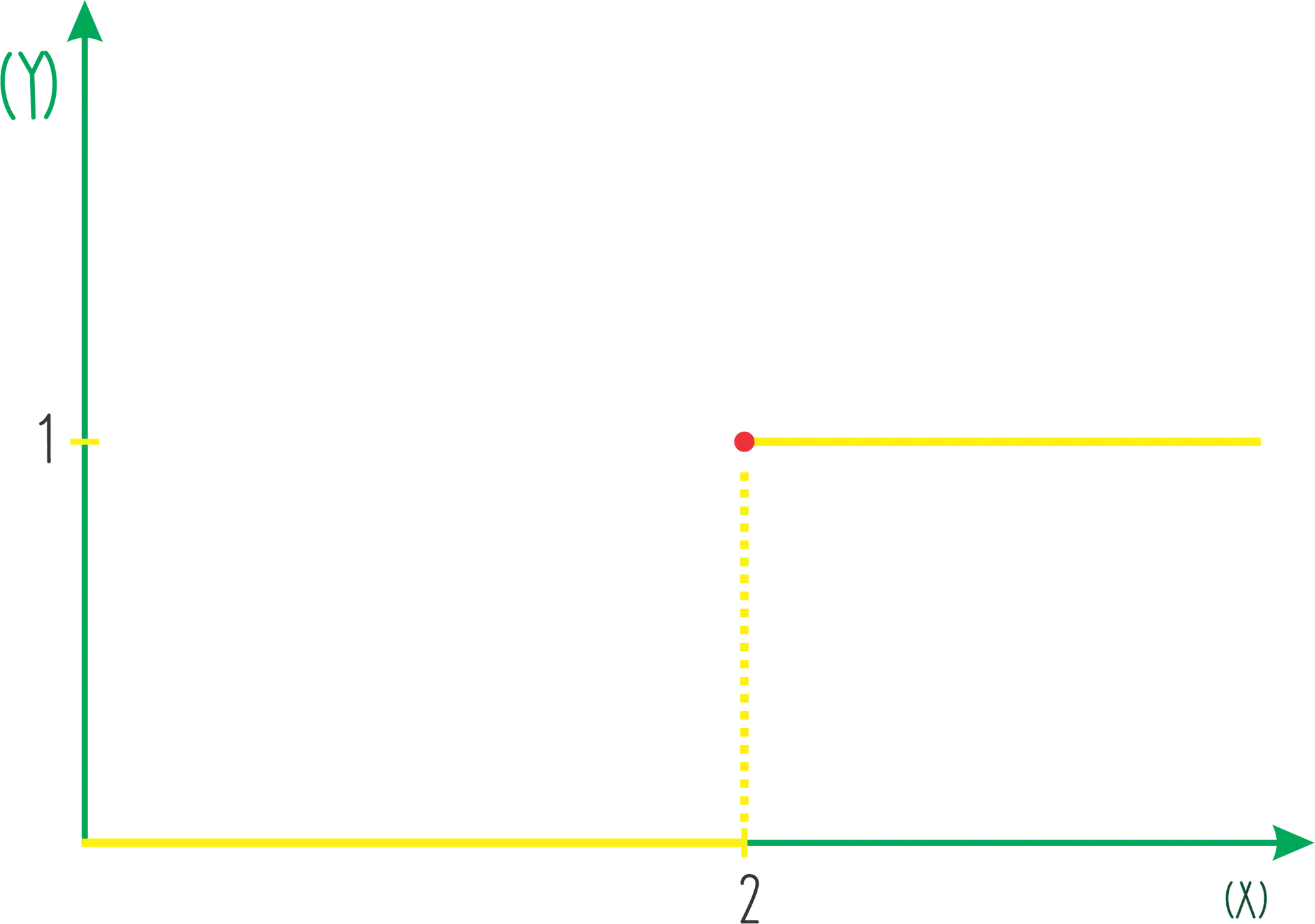
No gráfico podemos representar isso da seguinte forma:
Quer saber mais sobre a representação de funções degrau? Então se liga nesse vídeo 👇👇👇
Como Escrever uma Função usando Degrau
Pra a gente aprender como escrever uma função usando degrau, vamos fazer um exemplo! Se liga na função
A primeira coisa que vamos fazer é um rascunho do gráfico:
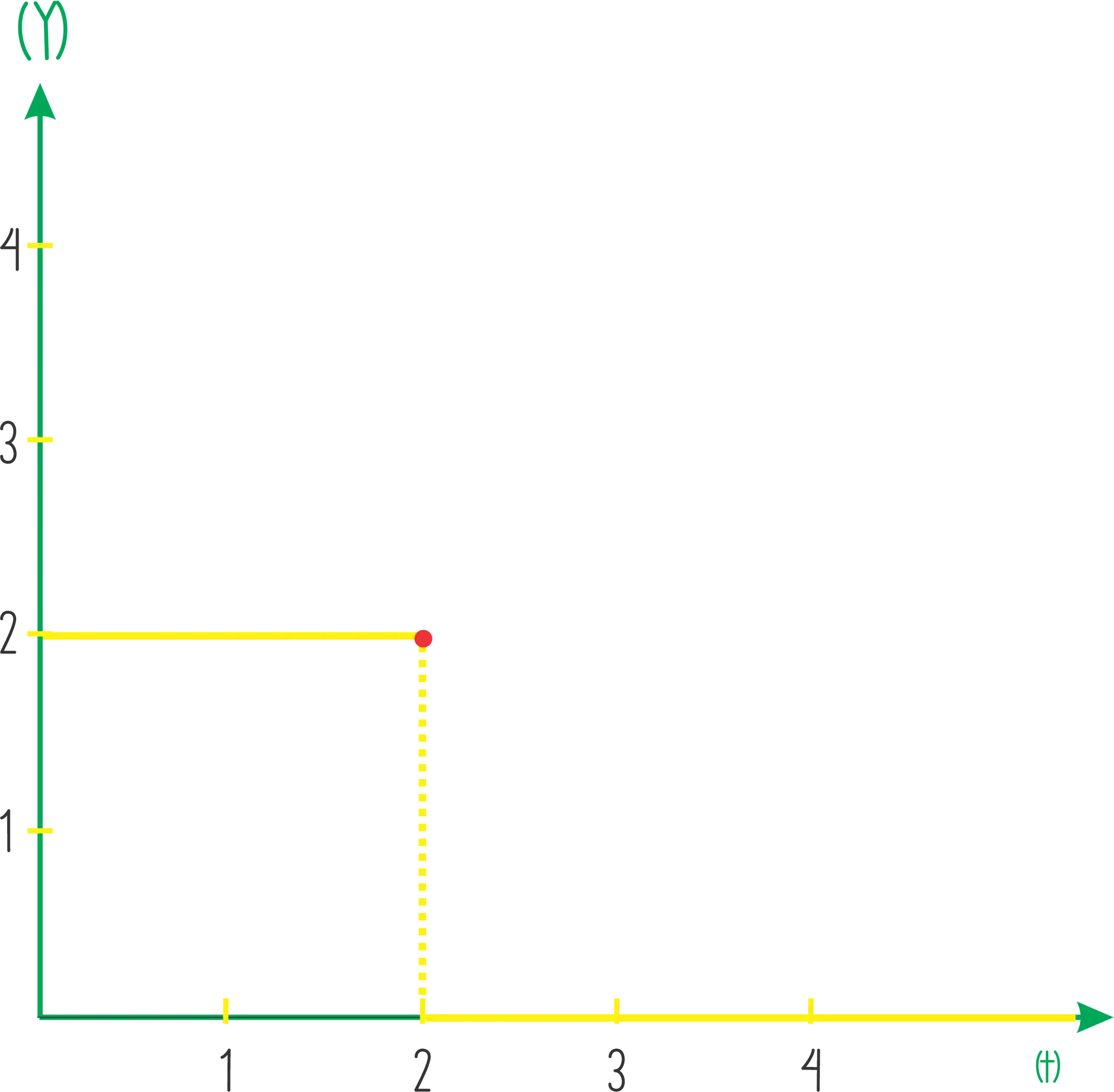
Podemos enxergar essa função de cima como sendo a subtração de duas funções. Na primeira teríamos
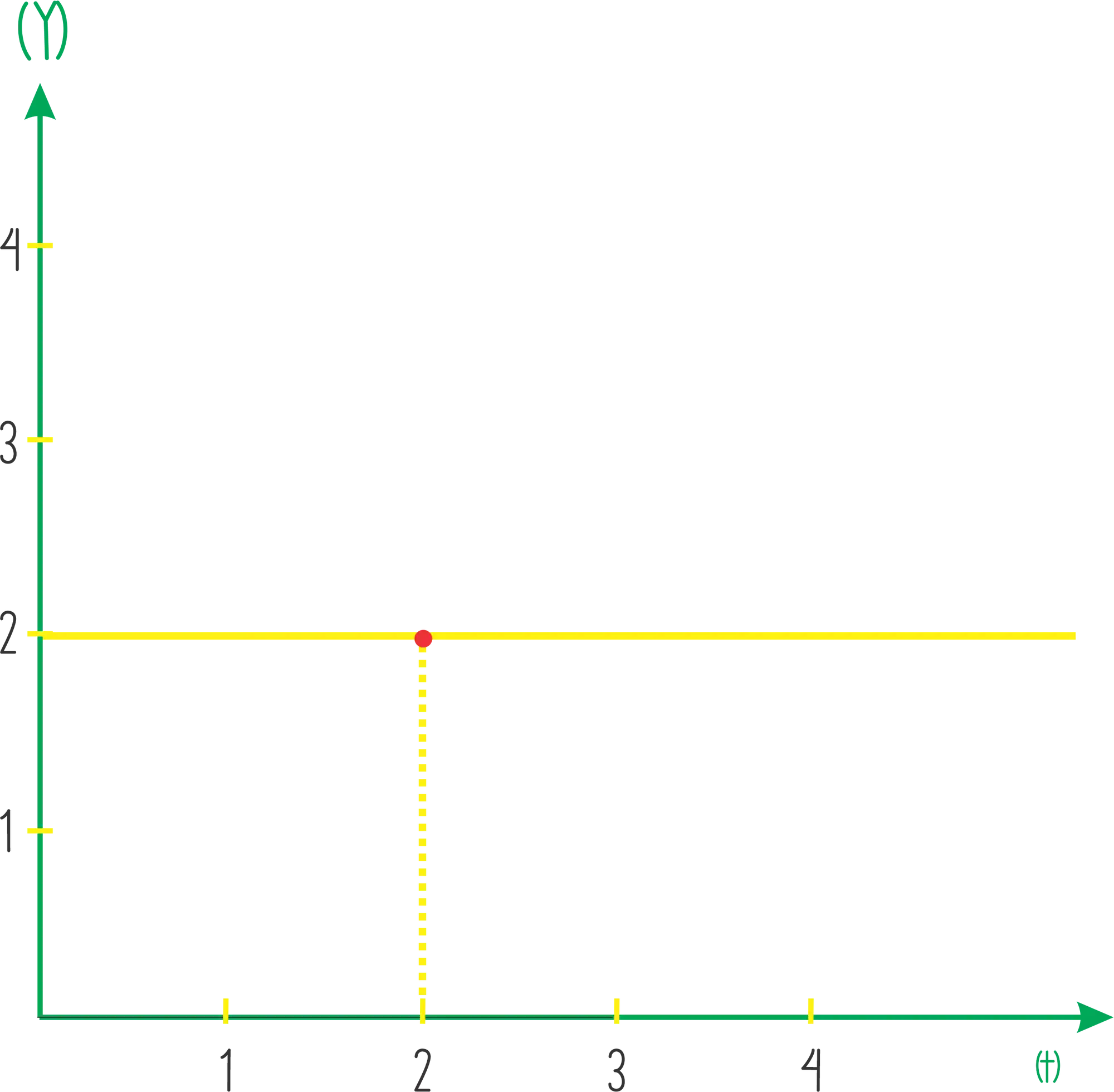
Lembra que a função que a gente quer escrever é zero a partir de
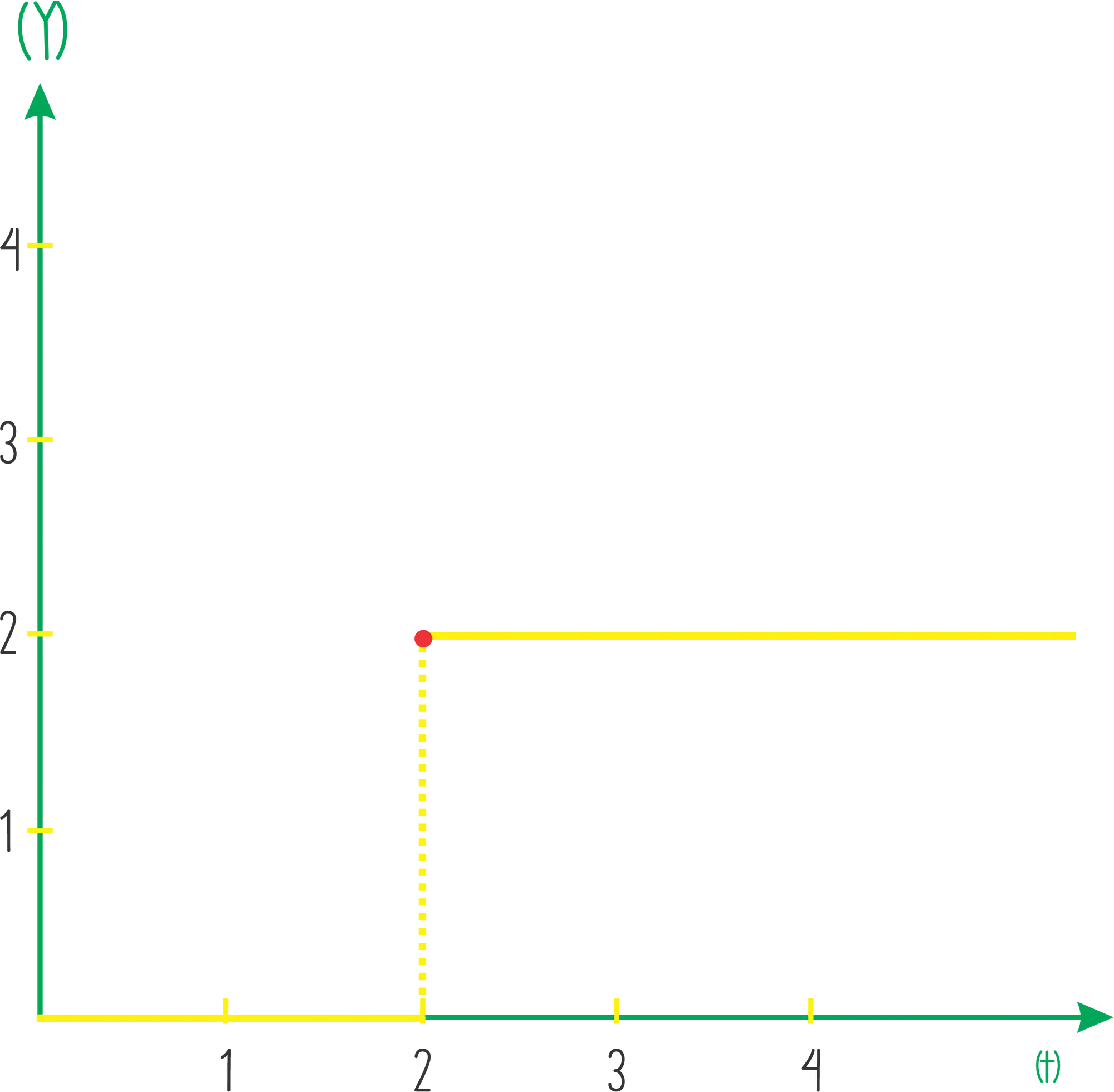
Agora vamos subtrair uma da outra:
Graficamente temos:
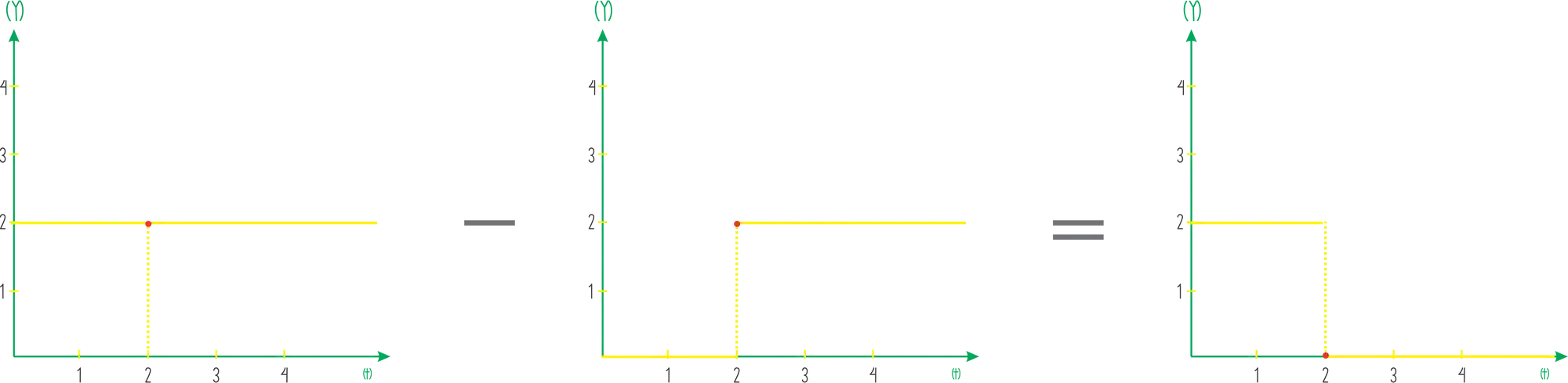
É chegamos na nossa função degrau! Agora vamos praticar com exercícios?