Uma solução aquosa que contém de A e de água é submetida a uma destilação diferencial. Qual o percentual da solução inicial deve ser destilado para que se obtenha um resíduo com de A? Sabendo que a volatilidade relativa média de A em relação à água é .
Passo 1
Bom, antes de tudo vamos entender o que esse enunciado está falando pra gente, beleza? Aqui nós temos uma solução aquosa formada por água e um componente A. Além disso o enunciado nos forneceu:
Repara que o enunciado não nos deu a quantidade da mistura, então vamos utilizar como base de cálculo que,
Além disso, vamos assumir que a solução é ideal, beleza?
E com essas informações nós vamos calcular o percentual da solução inicial que deve ser destilado para que se obtenha um resíduo com . Vamos lá!
Passo 2
Como a mistura é binária e consideramos solução ideal, podemos considerar constante e temos:
Para diferentes valores de obtemos o correspondente e com isso podemos encontrar a equação da linha de equilíbrio.
Então, o que vamos fazer agora é chutar valores de e encontrar a partir da equação de volatilidade relativa.

E com isso, fazendo o ajuste não linear, com auxílio da calculadora, conseguimos extrair a equação da linha de equilíbrio,
Onde o coeficiente de relação é,
Passo 3
Passo 4
Então, o que vamos fazer agora é chutar valores de e encontrar a partir da equação de volatilidade relativa. Por exemplo vamos considerar que,
Então,
Fazendo para vários valores temos,
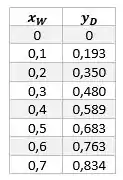
E com isso, fazendo o ajuste não linear, com auxílio da calculadora, conseguimos extrair a equação da linha de equilíbrio,
Onde o coeficiente de relação é,
Passo 5
Passo 6
Agora nós vamos utilizar a regra do trapézio.
Adequando essa equação ao enunciado temos,
Temos que a área abaixo da curva é numericamente igual ao valor da integral, que vai ser a área de um trapézio.
Passo 7
A destilação vai ocorrer de até e vamos poder traçar um gráfico com eixos .
Então, antes de tudo, vamos construir uma tabela a partir da equação de equilíbrio.

Já com os pontos definidos, podemos traçar o nosso gráfico.

Passo 8
Agora podemos calcular as áreas dos 3 trapézios,
Somando as três áreas, temos,
Que é o valor da integral,
Passo 9
Com isso, utilizando a base de cálculo de temos,
Que é a quantidade de mols que vai ficar dentro do tanque de destilação.
Por diferença, obtemos o percentual da solução inicial que deve ser destilado.
ou
Resposta
ou