Modele o processo de destilação em batelada em estágio único matematicamente.
Passo 1
Antes de começar a modelação matemática precisamos definir algumas hipóteses:
- O vapor de composição está em equilíbrio com o líquido remanescente no tanque no instante .
- A taxa de vaporização é constante. Logo, é constante.
Lembrando do desenho esquemático:
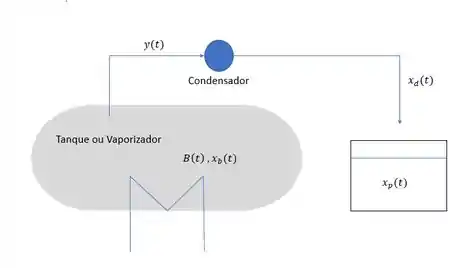
Passo 2
Com as hipóteses definidas, precisamos fazer um balanço de massa. Para isso, vamos fazer um balanço de massa que varie com o tempo, ou seja, transiente.
Para o balanço de Massa Global temos:
Para o balanço de Massa por Componente temos:
Resolvendo a multiplicação dentro da nossa derivada, obtemos que:
Podemos substituir e obter que:
Reorganizando essa equação, obtemos que:
Passo 3
Sabemos que , portanto . Substituindo na equação anterior e reorganizando, obtemos a seguinte equação:
Se integrarmos obtemos que: