Uma solução aquosa que contém de A e de água é submetida a uma destilação diferencial. Sabendo que a volatilidade relativa média de A em relação à água é . Encontre a equação da linha de equilíbrio.
Passo 1
Bom, antes de tudo vamos passar um raio X nesse enunciado, beleza? Aqui nós temos uma solução aquosa formada por água (dã) e um componente A. Além disso o enunciado nos forneceu:
Repara que o enunciado não nos deu a quantidade da mistura, então vamos utilizar como base de cálculo que,
Além disso, vamos assumir que a solução é ideal, beleza?
Passo 2
Como a mistura é binária e consideramos solução ideal, podemos considerar constante e usar a equação que já utilizamos várias vezes ao longo de operações.
Adaptando a nomenclatura para essa questão, temos:
Como a mistura é binária e consideramos solução ideal, podemos considerar constante e usar a equação que já utilizamos várias vezes ao longo de operações.
Para diferentes valores de obtemos o correspondente e com isso podemos encontrar a equação da linha de equilíbrio.
Passo 3
Então, o que vamos fazer agora é chutar valores de e encontrar a partir da equação de volatilidade relativa. Por exemplo vamos considerar que,
Então,
Fazendo para vários valores temos,
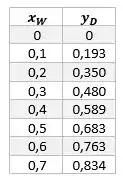
E com isso, fazendo o ajuste não linear, com auxílio da calculadora, conseguimos extrair a equação da linha de equilíbrio,
Onde o coeficiente de relação é,