Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Leis de Ohm

Ver Todos os Exercícios

Teoria

Fala aí! Bora conversar sobre as Leis de Ohm?!

Então, se liga nesse videozinho super completo que a gente preparou pra você 👇👇👇

📢 Clique para ver mais:

1° Lei de Ohm: Proporcionalidade entre Tensão e Corrente

“A primeira lei de Ohm afirma que uma corrente elétrica é gerada a partir de uma diferença de potencial (ddp) que está aplicada sobre o corpo, e esta corrente é proporcional a essa ddp.”

Ou seja:

Se aplicarmos uma diferença de potencial em dois terminais, fechando um circuito elétrico, a corrente gerada vai ser proporcional a essa ddp. Isso é, quanto maior a diferença de potencial, maior é a corrente que irá circular nesse circuito.

Podemos escrever então a fórmula da Primeira Lei de Ohm:

Onde:

  • é a diferença de potencial aplicada, também chamada de tensão e é medida em volts ;

  • é a corrente que foi gerada, medida em ampére ;

  • é a proporção entre a corrente e a tensão, ou seja, a resistência que o corpo oferece à passagem de corrente. Medida em ohms .

Representamos um circuito elétrico da seguinte forma:

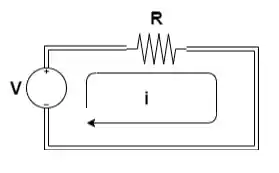
Circuito elétrico.
Circuito elétrico.

Primeira Lei de Ohm - Exercício Resolvido

Se eu tenho uma lâmpada cuja resistência é igual a e aplico uma tensão da tomada igual a , qual será a corrente que circulará para acender essa lâmpada?

Como a primeira lei de Ohm já diz:

Isolamos a corrente, :

Substituímos os dados:

Ou seja, a corrente que circulará para acender essa lâmpada será igual a .

2° Lei de Ohm: Variação da resistência

-Beleza, mas essa resistência depende de que?!


Excelente pergunta! E é o que a segunda lei de Ohm responde!

A resistência irá variar com o material do condutor e com a sua geometria. Eu te explico melhor!


Dá uma olhada na imagem abaixo:

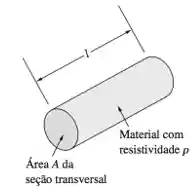
Material Condutor
Material Condutor

Quando eu digo que a resistência varia com a geometria, é porque ela é proporcional à área da secção transversal do condutor e inversamente proporcional ao seu comprimento . Agora, pra considerar o material do condutor, usamos uma constante chamada resistividade .

Dessa forma podemos escrever a fórmula da 2ª lei de ohm:

Desta forma, para um fio muito grande, a resistência aumenta, pois dificulta a passagem de corrente por um caminho tão longo. Por outro lado se eu tiver uma área muito grande, a corrente terá mais facilidade de passar pelo fio e a resistência R vai ser pequena.


Agora falando um pouco sobre a resistividade , como o próprio nome já diz ela resiste a passagem de corrente e aumenta a resistência. Então quanto maior for a resistivide, maior será a resistência.

Aqui temos uma tabelinha com os valores da resistividade de alguns materiais:

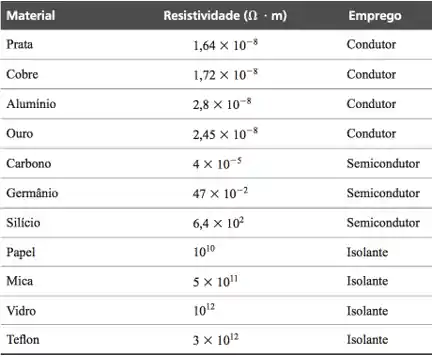
Resistividade de diferentes materiais.
Resistividade de diferentes materiais.

Segunda Lei de Ohm - Exercício Resolvido

Compare as resistências de dois fios condutores de mesmo material e área transversal, mas diferentes comprimentos:

Dados:

  • Fio 1:
    • Área da seção transversal: ²
    • Comprimento =
    • Resistividade:

  • Fio 2:
    • Área da seção transversal: ²
    • Comprimento =
    • Resistividade:

Vamos usar aqui a segunda lei de Ohm:

Para o primeiro fio, temos:

Para o segundo fio:


Percebemos que com o comprimento maior, aumentou a resistência. 😉

Agora que você já esta sacando tudo sobre a Lei de Ohm, vamos praticar com mais exercícios?!

2° Lei de Ohm: Variação da resistência

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Qual resistência de um resistor que conduz uma corrente de 10 A quando posto em uma d d p de 120 V ?

Passo 1

Primeiro vamos ver que circuito é esse:

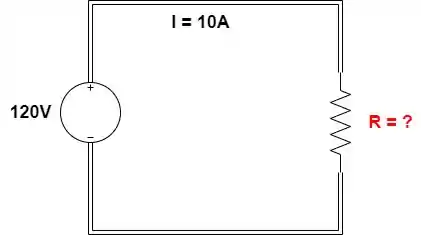
Passo 2

Aqui só precisamos usar a expressão da 1ª Lei de Ohm, se liga:

V = R I

Substituindo os valores do enunciado:

120 = R   .   10

E portanto:

R = 12   Ω

Resposta

R = 12 Ω

Exercício Resolvido #2

UFRJ, PF 2014.2, ME 8

Uma barra de cobre cilíndrica, de resistência elétrica R , comprimento L e seção reta A , é comprimida para a metade do seu comprimento original, sem que seu volume se altere.

Pode-se afirmar que o novo valor de sua resistência elétrica é:

a 4 R

b 2 R

c R / 2

d R / 4

e R

Passo 1

Os dados do problema são, inicialmente:

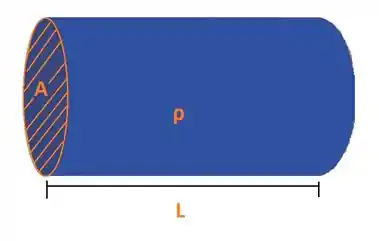
A resistência R , por definição é dada por:

R = ρ L A

Posteriormente, temos uma redução do comprimento, mas mantemos o volume:

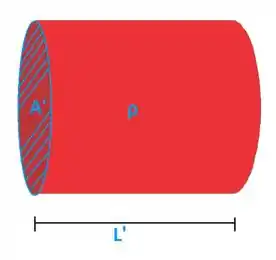
Precisamos primeiro encontrar as relações para L ' e A ' .

O volume inicial é igual a:

V = L A

O volume após a barra ser modificada é igual a:

V ' = L ' A '  

Mas como, ao ser comprimida, o seu volume não se altera, podemos dizer que:

V = L A = L ' A '

Onde L ' = L / 2 , logo:

L A = L A ' 2 → A ' = 2 A

Portanto, a nova resistência será dada por:

R ' = ρ L ' A ' = ρ L 2 2 A

R ' = ρ L 4 A → R ' = R 4

A opção certa é a letra d .

Resposta

d R / 4

Exercício Resolvido #3

Halliday/ Resnick, Fundamentos da Física Volume 3, 8ª ed. LTC, Cap. 26, pp. 160-15

Um fio de Nichrome (uma liga de níquel, cromo e ferro muito usada em elementos de aquecimento) tem 1,0   m de comprimento e 1,0   m m 2 de seção reta e conduz uma corrente de 4,0   A quando uma diferença de potencial de 2,0   V é aplicada a suas extremidades.

Calcule a condutividade σ do Nichrome.

Passo 1

Não fica preocupado, a condutividade σ (em Ω . m - 1 ) nada mais é do que o inverso da resistividade ρ (em Ω . m ):

σ = 1 ρ

E sabemos chegar na resistividade, não é mesmo? Através dos dados do circuito! Se você não está lembrando, vem comigo...

Pra começar, vamos usar a corrente e a diferença de potencial que o problema forneceu pra calcularmos a resistência.

A resistência é dada por:

R = V i

Onde:

V = 2,0   V

i = 4,0   A

Logo:

R = 2 4

R = 0,5   Ω

Passo 2

A resistência está associada com resistividade através da segunda Lei de Ohm:

R = ρ L A

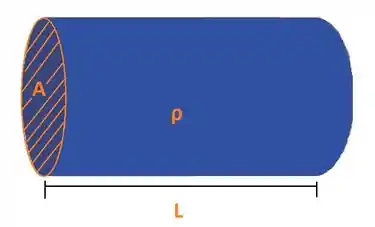
A resistência R é o produto entre a resistividade ρ e o comprimento do condutor L , dividido pela área da seção do condutor A !

Assim, a resistividade será:

ρ = R . A L

Onde os dados no enunciado são:

A = 1,0   m m 2 = 10 - 6   m 2

L = 1,0   m

Como a unidade da resistividade é Ohm-metro, precisamos passar todas as unidades para metro!

Nós já sabemos o valor da resistência que calculamos no passo anterior:

R = 0,5   Ω

Logo:

ρ = 0,5 × 10 - 6 1

ρ = 5,0 × 10 - 7   Ω . m

Achamos a resistividade!

Passo 3

Finalmente, a condutividade será o inverso da resistividade:

σ = 1 ρ

σ = 1 5,0 × 10 - 7

σ = 2,0 × 10 6   Ω . m - 1

Resposta

σ = 2,0 × 10 6   Ω . m - 1

Exercício Resolvido #4

(UEPA)

Os choques elétricos produzidos no corpo humano podem provocar efeitos que vão desde uma simples dor ou contração muscular, até paralisia respiratória ou fibrilação ventricular. Tais efeitos dependem de fatores como a intensidade de corrente elétrica, duração, resistência da porção do corpo envolvida. Suponha, por exemplo, um choque produzido por uma corrente de apenas 4   m A e que a resistência da porção do corpo envolvida seja de 3000   Ω . Então, podemos afirmar que o choque elétrico pode ter sido devido ao contato com:

  1. Uma pilha grande 1,5 V .
  2. Os contatos de uma lanterna contendo uma pilha grande de 6,0 V .
  3. Os contatos de uma bateria de automóvel de 12 V .
  4. Uma descarga elétrica produzida por um raio num dia de chuva.
  5. Os contatos de uma tomada de rede elétrica de 120   V .

Passo 1

Então galera… Esse é o tipo de questão que dá um susto na prova, a gente não sabe pra onde olhar, mas na real a dica é separar somente os dados importantes e ir! Não se assuste e vamos lá:

Os dados do choque são:

I   =   4   m A   =   4 * 10 - 3

R   = 3000   Ω .  

Passo 2

Agora basta usar a primeira lei de Ohm   ( V   =   R I ) pra calcular a tensão a qual a pessoa foi submetida!!

Lembrando que temos que deixar tudo no SI:

V   =   3000 *   4 *   10 - 3

V   =   12   V

Então, a pessoa teve contato com uma bateria de automóvel de 12   V . Letra C.

Resposta

V   =   12   V

Exercício Resolvido #5

Fundamentos de Circuitos Elétricos – 5ª Edição – Charles K. Alexander – Problema 2.64(ajustado)

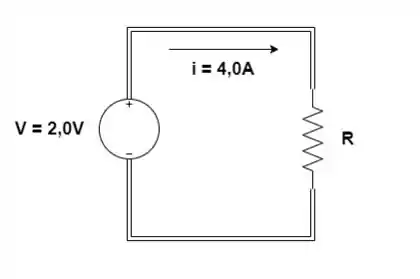
O potenciômetro (resistor ajustável) R x na Figura abaixo deve ser projetado para ajustar a corrente i x de 1   A a 10   A . Calcule os valores de R x para que isso aconteça.

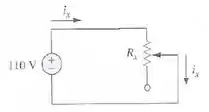
Passo 1

Temos aqui uma tensão de 110   V aplicada à uma resistência variável, portanto, aplicando a 1ª lei de Ohm, temos:

U = R I

110 = R x I

I = 11 0 R x

Passo 2

Agora queremos que a corrente varie entre 1   A e 10   A , para isso:

1 < I < 10

Substituindo a expressão encontrada:

1 < 11 0 R x < 10

Logo:

11 < R x < 11 0

Resposta

11 < R x < 110

Exercício Resolvido #6

USP, P2 2010, Questão 2

Um resistor com resistividade ρ , tem a forma de um cilindro oco de comprimento L e raios a e b . Calcule a resistência R e o módulo do vetor densidade de corrente J → no interior do resistor nos casos em que uma diferença de potencial V é aplicada:

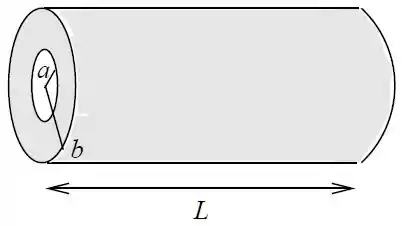
a ) entre as bases do cilindro.

b ) entre as superfícies interna de raio a e a externa de raio b .

Passo 1

a ) entre as bases do cilindro.

Por definição, a resistência de um resistor é dada por:

R = ρ L A

Nesse caro, A será a área da coroa circular de raios a e b .

A = π b 2 - a 2

Portanto:

R = ρ L π b 2 - a 2

Passo 2

Por definição, a densidade de corrente é dada por:

J = I A

Usando a definição de resistência, podemos dizer que:

J = V / R A → J = V R A

Lembrando que:

R = ρ L A → R A = ρ L

Logo:

J = V ρ L

Passo 3

b ) entre as superfícies interna de raio a e a externa de raio b .

A ideia aqui é bem parecida com o que fizemos antes, a diferença é que, como a corrente agora flui radialmente, vamos ter que mudar a forma de calcular a resistência.

Vamos começar dividindo o cilindro em camadas cilíndricas de largura d r . Cada cilindro terá resistência d R , dada por:

d R = ρ   d r A r

A r agora será a área lateral do cilindro.

A r = 2 π r L

Logo:

d R = ρ   d r 2 π r L

Pra encontrar uma expressão pra R , precisamos integrar esse cara, onde a < r < b :

R = ρ 2 π L   ∫ a b d r r

R = ρ 2 π L ln ⁡ b a

Passo 4

Pra calcular a densidade de corrente, vamos usar a mesma ideia que usamos anteriormente:

J = I A

J = V / R A → J = V R A

Lembrando que:

R = ρ L A → R A = ρ L

Logo:

J = V ρ L

Resposta

a )

R = ρ L π b 2 - a 2

J = V ρ L

b )

R = ρ 2 π L ln ⁡ b a

J = V ρ L

Exercício Resolvido #7

UERJ- Lista de Exercícios sobre Correntes Elétricas.

A figura é o gráfico corrente versus diferença de potencial para um material. Qual é a resistência do material?

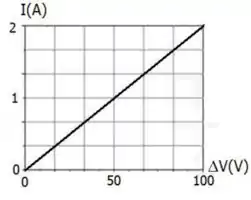
Passo 1

Para qualquer material condutor, temos que a cada ponto V = R . I , para um condutor ôhmico, temos que a resistência é constante, e no caso de um gráfico V por I é inclinação da reta. No gráfico mostrado, que é I por V , temos que a resistência será:

R = Δ V Δ I

R = 100 2 = 50 1 = 50   Ω

Resposta

R = 50   Ω

Exercício Resolvido #8

Autoria própria

Um ferro elétrico puxa da rede uma corrente igual à 20   A em uma linha com 110   V de tensão. Qual a condutância desse ferro elétrico?

Passo 1

Sabemos da 1ª Lei de Ohm que:

U = R I

Do enunciado, temos:

U = 110   V

E:

I = 20   A

Portanto, temos:

R = 110 20 = 5,5   Ω

É a resistência que queremos? Não né?

Passo 2

Para acharmos a condutância é fácil, basta inverter o valor da resistência!

G = 1 R ≅ 0,18   S

Resposta

0,18   S

Exercício Resolvido #9

(Efoa-MG)

Dois pedaços de fios de cobre cilíndricos têm o mesmo comprimento. Um tem diâmetro 2   m m e resistência elétrica R 2 , o outro tem diâmetro 3   m m e resistência elétrica   R 3 .

  1. Qual o valor da razao R 2 R 3 ?
  2. Nas instalações elétricas os fios mais grossos são utilizados para circuitos percorridos por correntes elétricas de maior intensidade. Qual justificativa, sob o ponto de vista da segurança dessas instalações, desse procedimento?

Passo 1

Letra a)

Vamos começar separando os dados:

Fio 1 :  d   =   2   m m

Fio 2 : d   =   3   m m

Como os dois são de cobre, o ρ   é o mesmo, e, como diz no enunciado, os l são os mesmos.

Passo 2

Utilizando a segunda lei de ohm:

R   =   ρ l A

R =   ρ l π r 2

E deixando em função do diâmetro…

R = ρ l π d 2 2

Passo 3

Achar R 2 e R 3

R 2 = ρ l π 2 2 2

R 2 =   ρ l π 1 2

R 3 = ρ l π 3 2 2

R 3 =   ρ l π 1,5 2

Passo 4

Achar a razão R 2 / R 3

R 2 R 3 =   ρ l π 1 2 ρ l π 1,5 2  

R 2 R 3 =     ρ l π *   2,25 π ρ

R 2 R 3 = 2,25   ( a d i m e n s i o n a l )

Passo 5

Letra b)

Se a resistência depende inversamente da área, se você coloca um fio mais grosso (área maior), a resistência será menor e quanto menor for a resistência, menos o fio vai aquecer e menor as chances de super-aquecimento e derretimento do fio. Logo, é mais seguro!!!

Resposta

a)

R 2 R 3 = 2,25   ( a d i m e n s i o n a l )

Exercício Resolvido #10

Fundamentos de Circuitos Elétricos – 5ª Edição – Charles K. Alexander – Exercício 2.3

Uma barra de silício tem 4 c m de comprimento com uma seção circular. Se a resistência da barra for 240 Ω à temperatura ambiente, qual o raio da seção transversal da barra?

ρ S i = 6.4 × 10 2 Ω   .   m

Passo 1

Aqui vamos usar diretamente a expressão da 2 ª lei de Ohm, se liga:

R = ρ L A

O enunciado nos dá os seguintes dados: a resistência R = 240 Ω , o comprimento da barra L = 4 c m e a resistividade do silício ρ S i = 6.4 × 10 2 Ω   .   m

Substituindo tudo, conseguimos isolar a área da seção transversal:

A = 6,4   .   10 2   .   4   .   10 - 2 240 = 0.10666 m 2

Passo 2

Agora precisamos achar o raio. Como é uma seção circular, temos:

A = π r 2

Substituindo a área encontrada:

r = 0.10666 π = 0.184 m = 18.4 c m

Resposta

r = 18.4 c m

Exercícios de Livros Relacionados

A tensão é medida em:WaatsAmpèresVoltsJoules por segundo
O inverso da resistência é:TensãoCorrenteCondutânciaCoulombs
A tensão e a corrente foram medidas nos terminais do dispositivo mostrado na Figura P2.14(a). Os valores de v e i são dados na tabela da Figura P2.14(b). Use os valores da tabela para construir um mod
A tensão em uma torradeira de 1,1k W que produz uma corrente de 10 A é: 11k V 1100V 110V 11V
Uma corrente de 4A carregando um material dielétrico acumulará de 24C após 6s .VerdadeiroFalso