Os lados e da escada da figura abaixo têm de comprimento e estão unidos por uma dobradiça no ponto . A barra horizontal tem de comprimento e está na metade da altura da escada. Um homem pesando sobe ao longo da escada. Supondo que não há atrito com o chão e desprezando a massa da escada, determine:
- a tensão da barra
- o módulo da força que o chão exerce sobre a escada no ponto
- o módulo da força que o chão exerce sobre a escada no ponto
( Sugestão: Isole partes da escada ao aplicar as condições de equilíbrio.)

Passo 1
Vamos analisar a figura e montar as equações de equilíbrio. Vamos seguir a sugestão do enunciado e isolar as partes da escada.
e são as força que o chão exerce em cada parte da escada.
é o peso do homem que podemos ver pela figura que tem uma distância de L/4 do ponto de contato entre as duas partes.
e são, respectivamente, a componente vertical e a componente horizontal que um lado da escada exerce no outro.
é a tração da corda.
Montamos então, o seguinte diagrama:
Lado esquerdo:
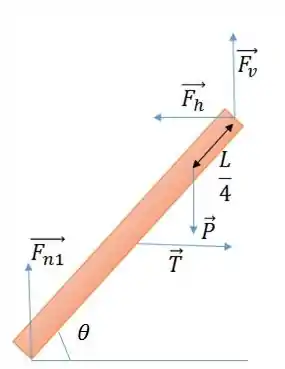
Lado direito:
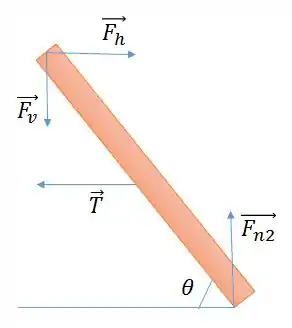
Passo 2
Vamos analisar agora, as equações de equilíbrio.
Aplicacando na parte esquerda:
Para analisar o torque resultante, vamos escolher o eixo de rotação no encontro entre as duas partes da escada. Vamos dar uma olhada na figura.
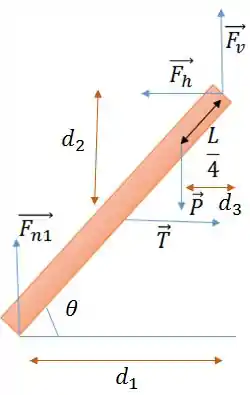
Precisamos das distâncias das forças que geram o torque até o eixo de rotação:
perpendicular a
perpendicular a
perpendicular a
Essas são as três forças que geram torque. e passam pelo eixo e não geram torque.
Por trigonometria, descobrimos os valores de , e em função do ângulo.
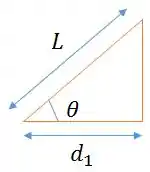
De forma, análoga, e .Agora que temos as distâncias, podemos aplicar a equação do torque, escolhendo o sentido anti-horário como positivo.
Passo 3
De forma análoga, podemos aplicar as condições de equilíbrio para o lado direito.
Escolhemos o eixo de rotação no encontro entre as duas partes. A única diferença dessa análise para a que fizemos anteriormente é que agora não temos a força peso do homem.
Passo 4
Montamos 5 equações de equilíbrio!
Precisamos resolvê-las para acharmos , e
Primeiro, manipulamos as equações :
Show! Agora substituímos por na equação .
Ajeitando a equação
Substituindo podemos deixar a equação VII em função de
Passo 5
Vamos descobrir agora qual o valor do ângulo
Para isso, vou montar um triângulo maroto ali. Se liga!
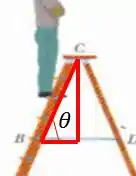
Criei um triângulo retângulo.
A hipotenusa dele vale metade do comprimento de um lado da escada
O cateto adjacente vale metade da barra horizontal BD
Logo,
Passo 6
OPA!
Agora que descobrimos o ângulo, podemos substituir na equação que encontramos para .
As continhas são chatas, mas é isso aí!
Passo 7
Tá acabando! Falta acharmos e .
Vou começar por .
Vimos lá em cima na equação que
Para achar , vou usar a equação lá de cima.