Equilíbrio Estático em Barras Inclinadas
Teoria
Equilíbrio Estático em Barras Inclinadas
Vamos falar agora do equilíbrio estático em barras inclinadas.
Você já deve estar bem familiarizado com as condições para equilíbrio estático:
- o somatório das forças externas ser zero
- o somatório dos torques externos em relação a qualquer ponto ser zero
Quando formos analisar um corpo inclinado, vamos utilizar essas mesmas equações. Só precisamos ter alguns cuidados.
Imagine uma gangorra de massa desprezível com dois blocos, um em cada extremidade. Ou melhor, a uma quase gangorra – não sou o melhor dos desenhos.
Supondo que ela esteja em equilíbrio estático, podemos usar as condições de equilíbrio.
Nesse caso, não tem nenhum mistério. É exatamente o que foi feito na teoria de equilíbrio estático num corpo horizontal.
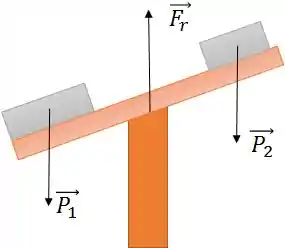
Isso você já sabia né!
Vamos agora para a outra condição de equilíbrio estático para o eixo central de rotação:
Aqui vamos precisar alguns cuidados.
Como o corpo está inclinado, para achar o módulo do momento de cada força precisamos achar a distância até o eixo de rotação que faça um ângulo de com a linha de ação da força.
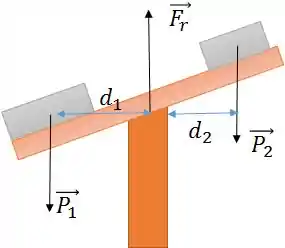
No caso do nosso exemplo, a força não causará torque, já que passa pelo eixo de rotação.
Para calcular o torque gerado por , precisamos achar o valor de , distância do eixo de rotação que faz com a linha de ação da força .
Da mesma forma, para calcular o torque gerado por , precisamos achar o valor de , distância do eixo de rotação que faz com a linha de ação da força .
Dessa forma, a equação
Definindo o sentido anti-horário como positivo
Achando d
Em alguns casos, vamos ter que descobrir o valor de .
Usando o exemplo da gangorra acima. Imagine que não é dado no problema.
Mas você tem o comprimento que no caso seria metade do comprimento da barra toda menos metade do comprimento do bloco.
Nesse caso, o problema vai fornecer um ângulo de inclinação.
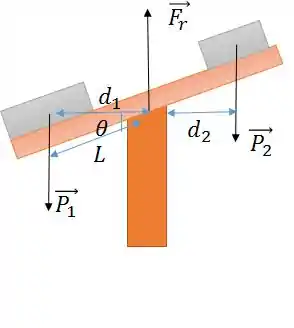
Show! Agora a gente monta um triângulo retângulo da massa e descobrimos o valor de .
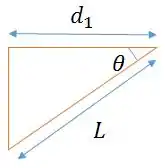
Vemos que é a hipotenusa. Logo, podemos ver que .
Casos de decomposição de força
Em alguns casos, vai ser necessário decompor forças.
Um exemplo é um bloco preso a uma corda em equilíbrio estático com um chão em atrito, um força normal e seu peso. Conforme a figura abaixo:
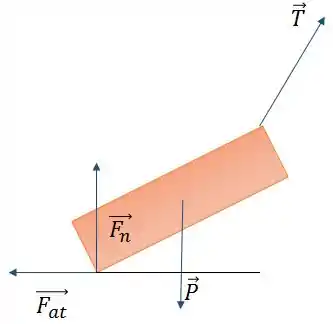
Quando formos analisar suas condições de equilíbrio, devemos ter cuidado em decompor .
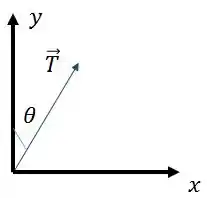
Podemos ver pelo desenho que:
Para calcular o torque gerado por essa força , podemos calcular o torque de cada componente do jeito que expliquei ali em cima – achando a distância do eixo até a linha de atuação da força que seja perpendicular. E, depois disso, somar os dois torques.
É isso!
Vamos para os exercícios?
Achando d
Casos de decomposição de força
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 2 , 8º ed. Rio de Janeiro: LTC , 2006, pp 19-15.
Para quebrar a casca de uma noz com um quebra-nozes, forças de pelo menos de módulo devem agir sobre a casca em ambos os lados. Para o quebra-nozes da figura abaixo, com distâncias e . Quais são as componentes das forças em cada cabo (aplicadas perpendicularmente aos cabos) que correspondem a esses ?
Passo 1
Vamos aplicar o equilíbrio do torque resultante.
Uma força de age sobre a casa a uma distância . Precisamos descobrir o valor da força a uma distância .
Vamos aplicar a fórmula do torque resultante, escolhendo o ponto de encontro entre os dois cabos como eixo de rotação.
A força é perpendicular a distância e gera torque no sentido anti-horário.
A força de é perpendicular a distância e gera torque no sentido horário.
Definindo por convenção o sentido anti-horário como positivo, montamos a equação.
=0
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 2 , 8º ed. Rio de Janeiro: LTC , 2006, pp 20-23.
Na figura abaixo, um bloco de é mantido em repouso através de um sistema de polias. O braço da pessoa está na vertical; o antebraço faz um ângulo com a horizontal. O antebraço e a mão têm uma massa conjunta de com um centro de massa a uma distância à frente do ponto de contato dos ossos do antebraço com o osso do braço (úmero). Um músculo (o tríceps) puxa o antebraço verticalmente para cima com uma força cujo ponto de aplicação está a uma distância atrás desse ponto de contato. A distância é . Quais são:
- O módulo da força exercida pelo tríceps sobre o antebraço
- O sentido (para cima ou para baixo) da força exercida pelo tríceps sobre o antebraço
- O módulo da força exercida pelo úmero sobre o antebraço
- O sentido (para cima ou para baixo) da força exercida pelo úmero sobre o antebraço
Passo 1
Como o bloco é mantido em repouso, podemos usar a equação de equilíbrio estável do torque.
Utilizando o ponto de contato dos ossos do antebraço com o osso do braço (úmero) como eixo de rotação, podemos aplicar:
Para aplicar essa fórmula, vamos achar as distâncias perpendiculares com a linha de ação das forças e calcular os momentos.
:
é a distância perpendicular do eixo de rotação até o centro de massa em que o peso do antebraço e da mão atuam.
peso da mão mais peso do antebraço
no sentido horário. Perceba que a massa do braço (antebraço + mão) faz o corpo girar no sentido horário
De forma análoga, achamos
=
força que o tríceps faz para cima
De forma análoga, achamos
Peso do bloco
s 30°. Nesse caso o sentido é anti-horário. Perceba que o bloco faz o corpo girar no sentido anti-horário.
Agora, definindo o sentido anti-horário como positivo, montamos a equação:
Passo 2
Vamos analisar o sentido dessa força agora.
Definimos que o sentido anti-horário é positivo. Então:
Logo, percebemos que o sentido do momento gerado pelo força do tríceps é horário. Para ele ser horário, sua força tem que ser para cima.
Repare na figura abaixo como se orienta o sentido do giro quando a força do tríceps é para cima.
Passo 3
Agora, podemos aplicar outra condição para o equilíbrio estático para descobrir , ou seja, a força do úmero.
Logo, o módulo de é igual a
Passo 4
O sentido é encontrado pelo sinal que achamos acima. Como orientamos as forças para cima como positivas e as forças negativas para baixo, a força do úmero tem sentido para baixo.
Resposta
- Para cima
- Para baixo
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 2 , 8º ed. Rio de Janeiro: LTC , 2006, pp 22-41.
Os lados e da escada da figura abaixo têm de comprimento e estão unidos por uma dobradiça no ponto . A barra horizontal tem de comprimento e está na metade da altura da escada. Um homem pesando sobe ao longo da escada. Supondo que não há atrito com o chão e desprezando a massa da escada, determine:
- a tensão da barra
- o módulo da força que o chão exerce sobre a escada no ponto
- o módulo da força que o chão exerce sobre a escada no ponto
( Sugestão: Isole partes da escada ao aplicar as condições de equilíbrio.)
Passo 1
Vamos analisar a figura e montar as equações de equilíbrio. Vamos seguir a sugestão do enunciado e isolar as partes da escada.
e são as força que o chão exerce em cada parte da escada.
é o peso do homem que podemos ver pela figura que tem uma distância de L/4 do ponto de contato entre as duas partes.
e são, respectivamente, a componente vertical e a componente horizontal que um lado da escada exerce no outro.
é a tração da corda.
Montamos então, o seguinte diagrama:
Lado esquerdo:
Lado direito:
Passo 2
Vamos analisar agora, as equações de equilíbrio.
Aplicacando na parte esquerda:
Para analisar o torque resultante, vamos escolher o eixo de rotação no encontro entre as duas partes da escada. Vamos dar uma olhada na figura.
Precisamos das distâncias das forças que geram o torque até o eixo de rotação:
perpendicular a
perpendicular a
perpendicular a
Essas são as três forças que geram torque. e passam pelo eixo e não geram torque.
Por trigonometria, descobrimos os valores de , e em função do ângulo.
De forma, análoga, e .Agora que temos as distâncias, podemos aplicar a equação do torque, escolhendo o sentido anti-horário como positivo.
Passo 3
De forma análoga, podemos aplicar as condições de equilíbrio para o lado direito.
Escolhemos o eixo de rotação no encontro entre as duas partes. A única diferença dessa análise para a que fizemos anteriormente é que agora não temos a força peso do homem.
Passo 4
Montamos 5 equações de equilíbrio!
Precisamos resolvê-las para acharmos , e
Primeiro, manipulamos as equações :
Show! Agora substituímos por na equação .
Ajeitando a equação
Substituindo podemos deixar a equação VII em função de
Passo 5
Vamos descobrir agora qual o valor do ângulo
Para isso, vou montar um triângulo maroto ali. Se liga!
Criei um triângulo retângulo.
A hipotenusa dele vale metade do comprimento de um lado da escada
O cateto adjacente vale metade da barra horizontal BD
Logo,
Passo 6
OPA!
Agora que descobrimos o ângulo, podemos substituir na equação que encontramos para .
As continhas são chatas, mas é isso aí!
Passo 7
Tá acabando! Falta acharmos e .
Vou começar por .
Vimos lá em cima na equação que
Para achar , vou usar a equação lá de cima.