Utilize agora equações de conservação para descrever o movimento de uma partícula em um fluido em movimento no sentido positivo do eixo x. Sabe-se que a gravidade aponta para baixo e perpendicular ao movimento do fluido.
Passo 1
Já vimos no exercício anterior que “para os lados” do movimento do fluido a partícula não se movimenta, ou seja, todo o movimento da partícula está concentrado nos eixos x e y, conforme definido abaixo:
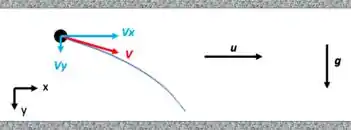
Daí, nem vou me preocupar com esse “terceiro” eixo. A partícula apenas apresenta velocidade nos eixos x e y.
Como o enunciado pede pra usarmos equações de conservação pra descrever o movimento, entra a matemática. Vamos precisar usar a equação do movimento da partícula:
Repara que já coloquei , já que o único campo de forças atuando é o gravitacional.
Como há movimento em dois eixos, abrimos essa equação para os dois eixos, x e y:
Passo 2
Com as hipóteses de:
- Escoamento unidimensional do fluido
- Desprezando a fase transiente do movimento da partícula
Vamos simplificar as equações:
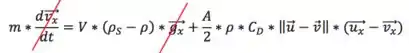
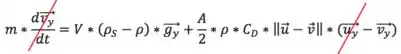
Dessa forma, ficamos com:
Olhando pra primeira equação, como vimos na na teoria, essa multiplicação só pode ser zero se
Já que sabemos que já que igualdade de vetores implicaria igualdade de módulo, direção e sentido, e sabemos (até pelo desenho mesmo) que isso não ocorre; esses dois vetores NÃO têm mesmas direção e sentido.
Então, já provamos que na direção do escoamento, fluido e partícula caminham com a mesma velocidade:
Passo 3
Olhando para a segunda equação que chegamos:
Calculando o esse módulo que aparece:
E já sabemos que daí
Além disso, , já que o fluido apenas se movimento no eixo x. Portanto:
Agora, substituindo por na segunda equação e o isolando:
Já igualei à pois esta é a expressão que achamos pra velocidade terminal de partícula sedimentando em fluido parado, com ,lá no tópico de velocidade terminal. Ou seja, provamos que na direção do campo, a partícula caminha com velocidade terminal:
Resposta
Ei, a resposta está no passo a passo :)