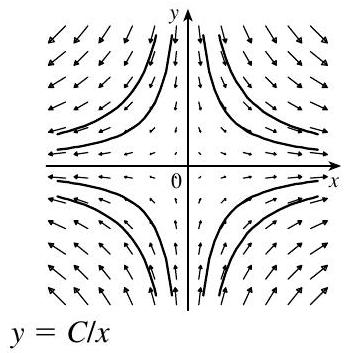
- Seja
\mathbf{F}(x, y)=\frac{-y \mathbf{i}+x \mathbf{j}}{x^{2}+y^{2}}.
(a) Mostre que
\partial P / \partial y=\partial Q / \partial x.
(b) Mostre que
\int_{C} \mathbf{F} \cdot d \mathbf{r} não é independente do caminho. [Dica: Calcule
\int_{C_{1}} \mathbf{F} \cdot d \mathbf{r} e
\int_{C_{2}} \mathbf{F} \cdot d \mathbf{r}, onde
C_{1} e
C_{2} são as metades superior e inferior do círculo
x^{2}+y^{2}=1 de
(1,0) a
(-1,0).] Isto contradiz o Teorema 6?
- (a) Suponha que
\mathbf{F} seja um campo vetorial inverso do quadrado, ou seja,
\mathbf{F}(\mathbf{r})=\frac{c \mathbf{r}}{|\mathbf{r}|^{3}}
para alguma constante
c, onde
\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}. Determine o trabalho realizado por
\mathbf{F} ao mover um objeto de um ponto
P_{1} por um caminho para um ponto
P_{2} em termos da distância
d_{1} e
d_{2} desses pontos à origem.
(b) Um exemplo de um campo de quadrado inverso é o campo gravitacional
\mathbf{F}=-(m M G) \mathbf{r} /|\mathbf{r}|^{3} discutido no Exemplo 4 na Seção 16.1. Use a parte (a) para determinar o trabalho realizado pelo campo gravitacional quando a Terra se move do afélio (em uma distância máxima de
1,52 \times 10^{8} \mathrm{~km} do Sol ) ao periélio (em uma distância mínima de
1,47 \times 10^{8} \mathrm{~km} ). (Use os valores
m=5,97 \times 10^{24} \mathrm{~kg}, M=1,99 \times 10^{30} \mathrm{~kg} \mathrm{e}
G=6,67 \times 10^{-11} \mathrm{~N} \cdot \mathrm{~m}^{2} / \mathrm{kg}^{2}.)
(b) Outro exemplo de campo inverso do quadrado é o campo elétrico
\mathbf{F}=\varepsilon q Q \mathbf{r} /|\mathbf{r}|^{3} discutido no Exemplo 5 da Seção 16.1. Suponha que um elétron com carga de
-1,6 \times 10^{-19} \mathrm{C} esteja localizado na origem. Uma carga positiva unitária é colocada à distância de
10^{-12} \mathrm{~m} do elétron e se move para uma posição que está à metade da distância original do elétron. Use a parte (a) para determinar o trabalho realizado pelo campo elétrico. (Use o valor
\varepsilon=8,985 \times 10^{9}.)
EXEMPLO
5 \operatorname{Se} \mathbf{F}(x, y)=(-y \mathbf{i}+x \mathbf{j}) /\left(x^{2}+y^{2}\right), mostre que
\int_{C} \mathbf{F} \cdot d \mathbf{r}=2 \pi para todo caminho fechado simples que circunde a origem.
SOLUÇÃO Como
C é um caminho fechado arbitrário contendo a origem em seu interior, é difícil calcular a integral dada diretamente. Então, vamos considerar um círculo anti-horário orientado
C^{\prime} com origem no centro e raio
a, onde
a é escolhido para ser pequeno o suficiente para que
C^{\prime} esteja contido em
C (ver Figura 11). Seja D a região limitada por
C e
C^{\prime}. Então a orientação positiva do limite é
C \cup\left(-C^{\prime}\right) e, aplicando a versão geral do Teorema de Green, temos
\begin{aligned} \int_{C} P d x+Q d y+\int_{-C^{\prime}} P d x+Q d y & =\iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d A \\\ & =\iint_{D}\left[\frac{y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}}-\frac{y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}}\right] d A=0 \end{aligned}
Logo,
\int_{C} P d x+Q d y=\int_{C^{\prime}} P d x+Q d y
isto é,
\int_{C} \mathbf{F} \cdot d \mathbf{r}=\int_{C^{\prime}} \mathbf{F} \cdot d \mathbf{r}
Agora podemos calcular facilmente essa última integral usando a parametrização dada por
\mathbf{r}(t)=a \cos t \mathbf{i}+a \operatorname{sen} t \mathbf{j}, 0 \leqslant t \leqslant 2 \pi. Logo,
\begin{aligned} \int_{C} \mathbf{F} \cdot d \mathbf{r} & =\int_{C^{\prime}} \mathbf{F} \cdot d \mathbf{r}=\int_{0}^{2 \pi} \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}^{\prime}(t) d t \\\ & =\int_{0}^{2 \pi} \frac{(-a \operatorname{sen} t)(-a \operatorname{sen} t)+(a \cos t)(a \cos t)}{a^{2} \cos ^{2} t+a^{2} \operatorname{sen}^{2} t} d t=\int_{0}^{2 \pi} d t=2 \pi \end{aligned}
Terminaremos esta seção utilizando o Teorema de Green para discutir um resultado enunciado na seção anterior.
ESBOÇO DA DEMONSTRAÇÃO DO TEOREMA 16.3.6 Assumimos que
\mathbf{F}=P \mathbf{i}+Q \mathbf{j} é um campo vetorial em uma região simplesmente conexa
D, que
P e
Q têm derivadas parciais de primeira ordem contínuas e que
\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x} \quad \text { em todo o } D
Se
C é um caminho fechado simples qualquer em
D e
R é a região envolvida por
C, o Teorema de Green nos dá
\oint_{C} \mathbf{F} \cdot d \mathbf{r}=\oint_{C} P d x+Q d y=\iint_{R}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d A=\iint_{R} 0 d A=0
Uma curva que não seja simples se autointercepta em um ou mais pontos e pode ser dividida em diversas curvas fechadas simples. Mostramos que as integrais de linha de
\mathbf{F} sobre essas curvas simples são todas 0 e , somando essas integrais, podemos ver que
\int_{C} \mathbf{F} \cdot d \mathbf{r}=0 para qualquer curva fechada
C. Portanto,
\int_{C} \mathbf{F} \cdot d \mathbf{r} é independente do caminho em
D pelo Teorema 16.3.3. Segue então que
\mathbf{F} é um campo vetorial conservativo.
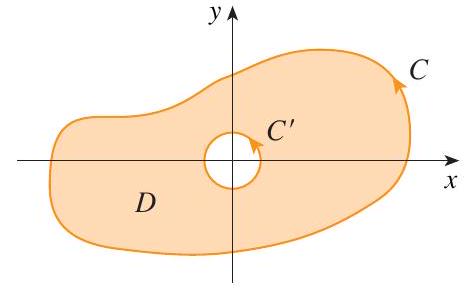
FIGURA 11
16.4 Exercícios
1-4 Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.
-
\oint_{C}(x-y) d x+(x+y) d y,
C é o círculo com centro na origem e raio 2
-
\oint_{C} x y d x+x^{2} d y,
C é o retângulo com vértices
(0,0)(3,0),(3,1) e
(0,1)
-
\oint_{C} x y d x+x^{2} y^{3} d y,
C é o triângulo com vértices
(0,0),(1,0) e
(1,2)
-
\quad \oint_{C} x^{2} y^{2} d x+x y d y, \quad C consiste no arco da parábola
y=x^{2} de
(0,0) a
(1,1) e os segmentos de reta de
(1,1) a
(0,1) e de
(0,1) a
(0,0)
5-10 Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
-
\int_{C} x y^{2} d x+2 x^{2} y d y,
C é o triângulo com vértices
(0,0),(2,2) e
(2,4)
-
\int_{C} \cos y d x+x^{2} \operatorname{sen} y d y,
C é o retângulo com vértices
(0,0),(5,0),(5,2) e
(0,2)
-
\int_{C}\left(y+e^{\sqrt{x}}\right) d x+\left(2 x+\cos y^{2}\right) d y,
C é o limite da região englobada pelas parábolas
y=x^{2} e
x=y^{2}
-
\int_{C} x e^{-2 x} d x+\left(x^{4}+2 x^{2} y^{2}\right) d y, C é o limite da região entre os círculos
x^{2}+y^{2}=1 e
x^{2}+y^{2}=4
-
\int_{C} y^{3} d x-x^{3} d y, C é o círculo
x^{2}+y^{2}=4
-
\int_{C}\left(1-y^{3}\right) d x+\left(x^{3}+e^{y^{2}}\right) d y, C é o limite da região entre os círculos
x^{2}+y^{2}=4 e
x^{2}+y^{2}=9
11-14 Use o teorema de Green para calcular
\int_{C} \mathbf{F} \cdot d \mathbf{r}. (Verifique a orientação da curva antes de aplicar o teorema.)
11.
\mathbf{F}(x, y)=\langle y \cos x-x y \operatorname{sen} x, x y+x \cos x\rangle,
C é o triângulo de
(0,0) a
(0,4) a
(2,0) a
(0,0)
12.
\mathbf{F}(x, y)=\left\langle e^{-x}+y^{2}, e^{-y}+x^{2}\right\rangle,
C consiste no arco da curva
y=\cos x de
(-\pi / 2,0) a
(\pi / 2,0) e o segmento de reta de
(\pi / 2,0) a
(-\pi / 2,0)
13.
\mathbf{F}(x, y)=\langle y-\cos y, x \operatorname{sen} y\rangle,
C é o círculo
(x-3)^{2}+(y+4)^{2}=4 orientado no sentido horário
14.
\mathbf{F}(x, y)=\left\langle\sqrt{x^{2}+1}, \operatorname{tg}^{-1} x\right\rangle, C é o triângulo de
(0,0) a
(1,1) a
(0,1) a
(0,0)15-16 Verifique o Teorema de Green usando um sistema de computação algébrica para calcular tanto a integral de linha como a integral dupla.
15.
P(x, y)=y^{2} e^{x}, \quad Q(x, y)=x^{2} e^{y},
C consiste no segmento de reta de
(-1,1) a
(1,1) seguido pelo arco da parábola
y=2-x^{2} de
(1,1) a
(-1,1)
16.
P(x, y)=2 x-x^{3} y^{5}, \quad Q(x, y)=x^{3} y^{8},
C é a elipse
4 x^{2}+y^{2}=4
17. Use o Teorema de Green para achar o trabalho realizado pela força
\mathbf{F}(x, y)=x(x+y) \mathbf{i}+x y^{2} \mathbf{j} ao mover uma partícula da origem ao longo do eixo
x para
(1,0), em seguida ao longo de um segmento de reta até ( 0,1 ), e então de volta à origem ao longo do eixo
y.
18. Uma partícula inicialmente no ponto
(-2,0) se move ao longo do eixo
x para
(2,0), e então ao longo da semicircunferência
y=\sqrt{4-x^{2}} até o ponto inicial. Utilize o Teorema de Green para determinar o trabalho realizado nessa partícula pelo campo de força
\mathbf{F}(x, y)=\left\langle x, x^{3}+3 x y^{2}\right\rangle.
19. Use uma das fórmulas em 5 para achar a área sob um arco da cicloide
x=t-\operatorname{sen} t, y=1-\cos t.
20. Se uma circunferência
C de raio 1 rola ao longo do interior da circunferência
x^{2}+y^{2}=16, um ponto fixo
P de
C descreve uma curva chamada epicicloide, com equações paramétricas
x=5 \cos t-\cos 5 t, y=5 \operatorname{sen} t-\operatorname{sen} 5 t. Faça o gráfico da epicicloide e use 5 para calcular a área da região que ela envolve.
21. (a) Se
C é o segmento de reta ligando o ponto
\left(x_{1}, y_{1}\right) ao ponto
\left(x_{2}, y_{2}\right), mostre que
\int_{C} x d y-y d x=x_{1} y_{2}-x_{2} y_{1}
(b) Se os vértices de um polígono, em sentido anti-horário, são
\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \ldots,\left(x_{n}, y_{n}\right) mostre que a área do polígono é
\begin{aligned} A=\frac{1}{2}[ & \left(x_{1} y_{2}-x_{2} y_{1}\right)+\left(x_{2} y_{3}-x_{3} y_{2}\right)+\cdots \\\ & \left.+\left(x_{n-1} y_{n}-x_{n} y_{n-1}\right)+\left(x_{n} y_{1}-x_{1} y_{n}\right)\right] \end{aligned}
(c) Encontre a área do pentágono com vértices
(0,0),(2,1),(1,
3),(0,2) e
(-1,1).
22. Seja
D a região limitada por um caminho fechado simples
C no plano
x y. Utilize o Teorema de Green para demonstrar que as coordenadas do centroide
(\bar{x}, \bar{y}) de
D são
\bar{x}=\frac{1}{2 A} \oint_{C} x^{2} d y \quad \bar{y}=-\frac{1}{2 A} \oint_{C} y^{2} d x
onde
A é a área de
D.
23. Use o Exercício 22 para encontrar o centroide de um quarto de uma região circular de raio
a.
24. Use o Exercício 22 para encontrar o centroide da região triangular de vértices
(0,0),(a, 0) e
(a, b), onde
a>0 e
b>0.
25. Uma lâmina plana com densidade constante
\rho(x, y)=\rho ocupa uma região do plano
x y limitada por um caminho fechado simples
C. Mostre que seus momentos de inércia em relação aos eixos são
I_{x}=-\frac{\rho}{3} \oint_{C} y^{3} d x \quad I_{y}=\frac{\rho}{3} \oint_{C} x^{3} d y
- Utilize o Exercício 25 para achar o momento de inércia de um círculo de raio a com densidade constante
\rho em relação a um diâmetro. (Compare com o Exemplo 4 da Seção 15.5.)
- Use o método do Exercício 5 para calcular
\int_{C} \mathbf{F} \cdot d \mathbf{r}, onde
\mathbf{F}(x, y)=\frac{2 x y \mathbf{i}+\left(y^{2}-x^{2}\right) \mathbf{j}}{\left(x^{2}+y^{2}\right)^{2}}
e
C é qualquer curva fechada simples positivamente orientada que envolve a origem.
28. Calcule
\int_{C} \mathbf{F} \cdot d \mathbf{r}, onde
\mathbf{F}(x, y)=\left\langle x^{2}+y, 3 x-y^{2}\right\rangle e
C é a fronteira positivamente orientada de uma região
D que tem área 6 .
29. Se
\mathbf{F} é o campo vetorial do Exemplo 5, mostre que
\int_{C} \mathbf{F} \cdot d \mathbf{r}=0 para todo caminho fechado simples que não passe pela origem e nem a circunde.
30. Complete a demonstração do Teorema de Green demonstrando a Equação 3.
31. Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.10.9) para o caso onde
f(x, y)=1 :
\iint_{R} d x d y=\iint_{S}\left|\frac{\partial(x, y)}{\partial(u, v)}\right| d u d v
Aqui,
R é a região do plano
x y que corresponde à região
S no plano
u v sob a transformação dada por
x=g(u, v), y=h(u, v).
[Dica: Observe que o lado esquerdo é
A(R) e aplique a primeira parte da Equação 5. Converta a integral de linha sobre
\partial R para uma integral sobre
\partial S e aplique o Teorema de Green no plano
u v.]
Portanto,
(\operatorname{rot} \mathbf{F}) \cdot \mathbf{k}=\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathbf{k} \cdot \mathbf{k}=\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}
e podemos reescrever a equação do Teorema de Green na forma vetorial
\oint_{C} \mathbf{F} \cdot d \mathbf{r}=\iint_{D}(\operatorname{rot} \mathbf{F}) \cdot \mathbf{k} d A
A Equação 12 expressa a integral de linha da componente tangencial de
\mathbf{F} ao longo de
C como uma integral dupla da componente vertical rotacional
\mathbf{F} sobre a região
D delimitada por
C. Vamos deduzir, agora, uma fórmula semelhante, envolvendo a componente normal de
\mathbf{F}.
Se
C é dada pela equação vetorial
\mathbf{r}(t)=x(t) \mathbf{i}+y(t) \mathbf{j} \quad a \leqslant t \leqslant b
então o vetor tangente unitário (veja a Seção 13.2) é
\mathbf{T}(t)=\frac{x^{\prime}(t)}{\left|\mathbf{r}^{\prime}(t)\right|} \mathbf{i}+\frac{y^{\prime}(t)}{\left|\mathbf{r}^{\prime}(t)\right|} \mathbf{j}
Você pode verificar que o vetor normal unitário externo a
C é dado por
\mathbf{n}(t)=\frac{y^{\prime}(t)}{\left|\mathbf{r}^{\prime}(t)\right|} \mathbf{i}-\frac{x^{\prime}(t)}{\left|\mathbf{r}^{\prime}(t)\right|} \mathbf{j}
(Veja a Figura 2). Então, da Equação 16.2.3, temos
\begin{aligned} \oint_{C} \mathbf{F} \cdot \mathbf{n} d s & =\int_{a}^{b}(\mathbf{F} \cdot \mathbf{n})(t)\left|\mathbf{r}^{\prime}(t)\right| d t \\\ & =\int_{a}^{b}\left[\frac{P(x(t), y(t)) y^{\prime}(t)}{\left|\mathbf{r}^{\prime}(t)\right|}-\frac{Q(x(t), y(t)) x^{\prime}(t)}{\left|\mathbf{r}^{\prime}(t)\right|}\right]\left|\mathbf{r}^{\prime}(t)\right| d t \\\ & =\int_{a}^{b} P(x(t), y(t)) y^{\prime}(t) d t-Q(x(t), y(t)) x^{\prime}(t) d t \\\ & =\int_{C} P d y-Q d x=\iint_{D}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right) d A \end{aligned}
FIGURA 2
pelo Teorema de Green. Mas o integrando na integral dupla é o divergente de
\mathbf{F}. Logo, temos uma segunda forma vetorial do Teorema de Green:
\oint_{C} \mathbf{F} \cdot \mathbf{n} d s=\iint_{D} \operatorname{div} \mathbf{F}(x, y) d A
Essa versão diz que a integral de linha da componente normal de
\mathbf{F} ao longo de
C é igual à integral dupla do divergente de
\mathbf{F} na região
D delimitada por
C.
16.5 Exercícios
1-8 Determine (a) o rotacional e (b) o divergente do campo vetorial.
-
\mathbf{F}(x, y, z)=x y z \mathbf{i}-x^{2} y \mathbf{k}
-
\quad \mathbf{F}(x, y, z)=x^{2} y z \mathbf{i}+x y^{2} z \mathbf{j}+x y z^{2} \mathbf{k}
-
\mathbf{F}(x, y, z)=x y e^{z} \mathbf{i}+\mathrm{yz} e^{x} \mathbf{k}
-
\quad \mathbf{F}(x, y, z)=\operatorname{sen} y z \mathbf{i}+\operatorname{sen} z x \mathbf{j}+\operatorname{sen} x y \mathbf{k}
-
\quad \mathbf{F}(x, y, z)=\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})
-
\quad \mathbf{F}(x, y, z)=e^{x y} \operatorname{sen} z \mathbf{j}+y \operatorname{tg}^{-1}(x / z) \mathbf{k}
-
\mathbf{F}(x, y, z)=\left\langle e^{x} \operatorname{sen} y, e^{y} \operatorname{sen} \mathrm{z}, e^{z} \operatorname{sen} \mathrm{x}\right\rangle
-
\quad \mathbf{F}(x, y, z)=\left\langle\frac{x}{y}, \frac{y}{z}, \frac{z}{x}\right\rangle
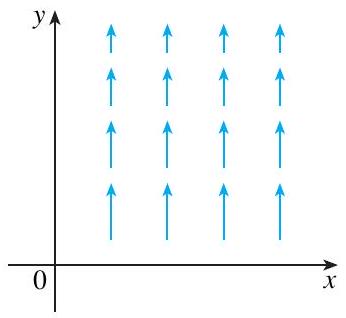
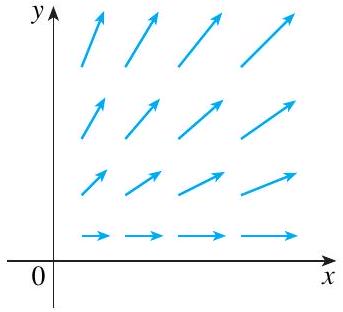
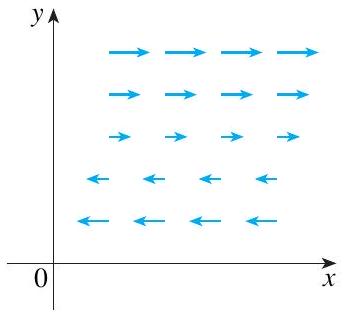
9-11 O campo vetorial
\mathbf{F} é mostrado no plano
x y e é o mesmo em todos os planos horizontais (em outras palavras,
\mathbf{F} é independente de
z e sua componente
z é 0 ).
(a) O div
\mathbf{F} será positivo, negativo ou nulo? Explique.
(b) Determine se
\operatorname{rot} \mathbf{F}=\mathbf{0}. Se não, em que direção
\operatorname{rot} \mathbf{F} aponta?
9.
10.
11.
12. Seja
f um campo escalar e
\mathbf{F} um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
(a)
\operatorname{rot} f
(b)
\operatorname{grad} f
(c)
\operatorname{div} \mathbf{F}
(d)
\operatorname{rot}(\operatorname{grad} f)
(e)
\operatorname{grad} \mathbf{F}
(f)
\operatorname{grad}(\operatorname{div} \mathbf{F})
(g)
\operatorname{div}(\operatorname{grad} f)
(h)
\operatorname{grad}(\operatorname{div} f)
(i)
\operatorname{rot}(\operatorname{rot} \mathbf{F})
(j)
\operatorname{div}(\operatorname{div} \mathbf{F})
(k)
(\operatorname{grad} f) \times(\operatorname{div} \mathbf{F})
(l)
\operatorname{div}(\operatorname{rot}(\operatorname{grad} f))13-18 Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função
f tal que
\mathbf{F}=\nabla f.
13.
\mathbf{F}(x, y, z)=y^{2} z^{3} \mathbf{i}+2 x y z^{3} \mathbf{j}+3 x y^{2} z^{2} \mathbf{k}
14.
\mathbf{F}(x, y, z)=x y z^{2} \mathbf{i}+x^{2} y z^{2} \mathbf{j}+x^{2} y^{2} z \mathbf{k}
15.
\mathbf{F}(x, y, z)=3 x y^{2} z^{2} \mathbf{i}+2 x^{2} y z^{3} \mathbf{j}+3 x^{2} y^{2} z^{2} \mathbf{k}
16.
\mathbf{F}(x, y, z)=\mathbf{i}+\operatorname{sen} z \mathbf{j}+y \cos z \mathbf{k}
17.
\mathbf{F}(x, y, z)=e^{y z} \mathbf{i}+x z e^{y z} \mathbf{j}+x y e^{y z} \mathbf{k}
18.
\mathbf{F}(x, y, z)=e^{x} \operatorname{sen} y z \mathbf{i}+z e^{x} \cos y z \mathbf{j}+y e^{x} \cos y z \mathbf{k}
19. Existe um campo vetorial
\mathbf{G} em
\mathbb{R}^{3} tal que
\operatorname{rot} \mathbf{G}=\langle x \operatorname{sen} y, \cos y, z-x y\rangle ? Explique.
20. Existe um campo vetorial
\mathbf{G} em
\mathbb{R}^{3} tal que rot
\mathbf{G}=\left\langle x y z,-y^{2} z, y z^{2}\right\rangle ? Explique.
21. Mostre que qualquer campo vetorial da forma
\mathbf{F}(x, y, z)=f(x) \mathbf{i}+g(y) \mathbf{j}+h(z) \mathbf{k} onde
f, g e
h são diferenciáveis, é irrotacional.
- Mostre que qualquer campo vetorial da forma
\mathbf{F}(x, y, z)=f(y, z) \mathbf{i}+g(x, z) \mathbf{j}+h(x, y) \mathbf{k}
é incompressível.
23-29 Demonstre a identidade, admitindo que as derivadas parciais apropriadas existem e são contínuas. Se
f for um campo escalar e
\mathbf{F}, \mathbf{G} forem campos vetoriais, então
f \mathbf{F}, \mathbf{F} \cdot \mathbf{G} e
\mathbf{F} \times \mathbf{G} serão definidos por
\begin{aligned} (f \mathbf{F})(x, y, z) & =f(x, y, z) \mathbf{F}(x, y, z) \\\ (\mathbf{F} \cdot \mathbf{G})(x, y, z) & =\mathbf{F}(x, y, z) \cdot \mathbf{G}(x, y, z) \\\ (\mathbf{F} \times \mathbf{G})(x, y, z) & =\mathbf{F}(x, y, z) \times \mathbf{G}(x, y, z) \end{aligned}
23 \operatorname{div}(\mathbf{F}+\mathbf{G})=\operatorname{div} \mathbf{F}+\operatorname{div} \mathbf{G}
24.
\operatorname{rot}(\mathbf{F}+\mathbf{G})=\operatorname{rot} \mathbf{F}+\operatorname{rot} \mathbf{G}
25.
\operatorname{div}(f \mathbf{F})=f \operatorname{div} \mathbf{F}+\mathbf{F} \cdot \nabla f
26.
\operatorname{rot}(f \mathbf{F})=f \operatorname{rot} \mathbf{F}+(\nabla f) \times \mathbf{F}
27.
\operatorname{div}(\mathbf{F} \times \mathbf{G})=\mathbf{G} \cdot \operatorname{rot} \mathbf{F}-\mathbf{F} \cdot \operatorname{rot} \mathbf{G}
28.
\operatorname{div}(\nabla f \times \nabla g)=0
29.
\operatorname{rot}(\operatorname{rot} \mathbf{F})=\operatorname{grad}(\operatorname{div} \mathbf{F})-\nabla^{2} \mathbf{F}
30-32 Sejam
\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k} e
r=|\mathbf{r}|.
30. Verifique as identidades.
(a)
\nabla \cdot \mathbf{r}=3
(b)
\nabla \cdot(r \mathbf{r})=4 r
(c)
\nabla^{2} r^{3}=12 r
31. Verifique as identidades.
(a)
\nabla r=\mathbf{r} / r
(b)
\nabla \times \mathbf{r}=\mathbf{0}
(c)
\nabla(1 / r)=-\mathbf{r} / r^{3}
(d)
\nabla \ln r=\mathbf{r} / r^{2}
32. Se
\mathbf{F}=\mathbf{r} / r^{p}, determine
\operatorname{div} \mathbf{F}. Existe um valor de
p para que
\operatorname{div} \mathbf{F}=0 ?
33. Use o Teorema de Green na forma da Equação 13 para demonstrar a primeira identidade de Green:
\iint_{D} f \nabla^{2} g d A=\oint_{C} f(\nabla g) \cdot \mathbf{n} d s-\iint_{D} \nabla f \cdot \nabla g d A
onde
D e
C satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de
f e
g existem e são contínuas. (A quantidade
\nabla g \cdot \mathbf{n}=D_{\mathbf{n}} g aparece na integral de linha. Essa é a derivada direcional na direção do vetor normal
\mathbf{n} e é chamada derivada normal de g.)
34. Use a primeira identidade de Green (Exercício 33) para demonstrar a segunda identidade de Green:
\iint_{D}\left(f \nabla^{2} g-g \nabla^{2} f\right) d A=\oint_{C}(f \nabla g-g \nabla f) \cdot \mathbf{n} d s
onde
D e
C satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de
f e
g existem e são contínuas.
35. Lembre-se, da Seção 14.3, de que uma função
g é chamada harmônica em
D se satisfaz a equação de Laplace, isto é,
\nabla^{2} g=0 em
D. Utilize primeira identidade de Green (com as mesmas hipóteses que no Exercício 33) para mostrar que se
g é harmônica em
D, então
\oint_{C} D_{\mathbf{n}} g d s=0. Aqui,
D_{\mathbf{n}} g é a derivada normal de
g definida no Exercício 33.
36. Use a primeira identidade de Green para mostrar que se
f for harmônica em
D, e se
f(x, y)=0 na curva limite
C, então
\iint_{D}|\nabla f|^{2} d A=0. (Suponha que são válidas as mesmas hipóteses que no Exercício 33.)
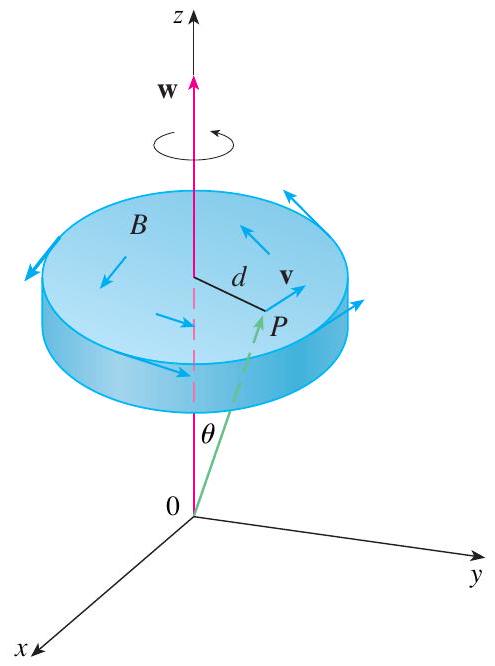
37. Este exercício ilustra a relação entre vetor rotacional e rotações. Seja
B ser um corpo rígido girando sobre o eixo
z. A rotação
pode ser descrita pelo vetor
\mathbf{w}=\omega \mathbf{k}, onde
\omega é a velocidade angular de
B, ou seja, a velocidade tangencial de qualquer ponto
P em
B dividida pela distância
d do eixo de rotação. Seja
\mathbf{r}=\langle x, y, z\rangle o vetor posição de
P.
(a) Considerando o ângulo
\theta da figura, mostre que o campo de velocidade de
B é dado por
\mathbf{v}=\mathbf{w} \times \mathbf{r}.
(b) Mostre que
\mathbf{v}=-\omega y \mathbf{i}+\omega x \mathbf{j}.
(c) Mostre que
\operatorname{rot} \mathbf{v}=2 \mathbf{w}.
38. As equações de Maxwell relacionam o campo elétrico E e o campo magnético
\mathbf{H}, quando eles variam com o tempo em uma região que não contenha carga nem corrente, como segue:
\operatorname{div} \mathbf{E}=0 \quad \operatorname{div} \mathbf{H}=0
\operatorname{rot} \mathbf{E}=-\frac{1}{c} \frac{\partial \mathbf{H}}{\partial t} \quad \operatorname{rot} \mathbf{H}=\frac{1}{c} \frac{\partial \mathbf{E}}{\partial t}
onde
c é a velocidade da luz. Use essas equações para demonstrar o seguinte:
(a)
\nabla \times(\nabla \times \mathbf{E})=-\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}
(b)
\nabla \times(\nabla \times \mathbf{H})=-\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{H}}{\partial t^{2}}
(c)
\nabla^{2} \mathbf{E}=\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{E}}{\partial t^{2}} \quad [Sugestão: Use o Exercício 29.]
(d)
\nabla^{2} \mathbf{H}=\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{H}}{\partial t^{2}}
39. Vimos que todos os campos vetoriais da forma
\mathbf{F}=\nabla g satisfazem a equação rot
\mathbf{F}=\mathbf{0} e que todos os campos vetoriais da forma
\mathbf{F}=\operatorname{rot} \mathbf{G} satisfazem a equação
\operatorname{div} \mathbf{F}=0 (supondo a continuidade das correspondentes derivadas parciais). Isto sugere a pergunta: existe alguma equação que todas as funções da forma
f=\operatorname{div} \mathbf{G} devam satisfazer? Mostre que a resposta para essa pergunta é “Não” demonstrando que toda função contínua
f em
\mathbb{R}^{3} é a divergência de algum campo de vetores. [Dica: Seja
\mathbf{G}(x, y, z)=\langle g(x, y, z), 0,0\rangle, onde
g(x, y, z)=\int_{0}^{x} f(t, y, z) d t.]
16.6 Superfícies Parametrizadas e suas Áreas
Até agora temos considerado tipos especiais de superfícies: cilindros, superfícies quádricas, gráficos de funções de duas variáveis e superfícies de nível de funções de três variáveis. Aqui, usaremos funções vetoriais para descrever superfícies mais gerais, chamadas superfícies parametrizadas e calcularemos suas áreas. A seguir, tomaremos a fórmula para a área de superfícies gerais e veremos como se aplica a superfícies especiais.
Superfícies Parametrizadas
De modo muito semelhante à nossa descrição de curvas espaciais por uma função vetorial
\mathbf{r}(t) de um único parâmetro
t, podemos descrever uma superfície por uma função vetorial
\mathbf{r}(u, v) de dois parâmetros
u e
v. Suponhamos que
\mathbf{r}(u, v)=x(u, v) \mathbf{i}+y(u, v) \mathbf{j}+z(u, v) \mathbf{k}
seja uma função a valores vetoriais definida sobre uma região
D do plano
u v. Então
x, y e
z, os componentes de funções de
\mathbf{r}, serão funções das duas variáveis
u e
v com domínio
D. O conjunto de todos os pontos
(x, y, z) em
\mathbb{R}^{3} tal que
x=x(u, v) \quad y=y(u, v) \quad z=z(u, v)
e (
u, v ) varia ao longo de
D, é chamado de superfície parametrizada
S e Equações 2 são chamados equações parametrizadas de
S. Cada escolha de
u e
v resulta um ponto em
S; fazendo todas as escolhas, temos todos os pontos de
S. Em outras palavras, a superfície é
35. (a)