Exercício 8. [resolução]
De acordo com a teoria da relatividade, o comprimento de um objeto, por exemplo, um foguete, parece a um observador depender da velocidade em que o objeto viaja em relação ao próprio observador. Se o observador medir o comprimento
do foguete em repouso, então, à velocidade
, o comprimento parecerá
em que
é a velocidade da luz no vácuo, cerca de
. Essa equação é a fórmula da contração de Lorentz. O que acontece com
à medida que
aumenta? Determine
. Por que o limite lateral à esquerda foi necessário?
1 Resoluções dos exercícios:
Resolução do Ex. 1 [voltar]
a)
(tendendo por valores positivos).
b)
(tendendo por valores negativos).
c)
5, portanto:
lim x -infty 5+1x+3x^2=5.
d)
2-undersetsubstackx 0 x +infty1x undersetx +inftylongrightarrow 2, portanto:
lim x +infty 2-1x.
e)
2 x+1x+3= & underbrace2 x+6x+3x +3-5x+3=2-underbrace5x+3x +infty- x +infty 2^+ & =2(x+3)x+3
f)
2 x+1x+3=2 x+6x+3-5x+3=2-underbrace5x+3x +infty undersetx +inftylongrightarrow 2^+, portanto:
lim x -infty 2 x+1x+3=2.
g)
x^2-2 x+33 x^2+x+1=x^2 cdot(1-2x+3x^2)3 x^2 cdot(1+13 x+13 x^2)=1 cdot overbrace(1-2x+3x^2)^(underbracelongrightarrowx -infty 13 cdot(1+13 x+13 x^2) undersetx -inftylongrightarrow 13.
Todas as funções racionais podem ser tratadas de maneira similar aos casos
e ),
f ) e
g ).
Na prática, é bom saber a regra geral seguinte:
Sendo dois polinômios
am x^m+cdots+a1 x+a0 e
bn x^n+cdots+b1 x+b0 temos:
lim x +infty am x^m+cdots+a1 x+a0bn x^n+cdots+b1 x+b0 & =lim x +infty am x^mbn lim x -infty am x^m+cdots+a1 x+a0bn x^n+cdots+b1 x+b0 & =lim x -infty am x^mbn x^n
Implicitamente, nestas formulas,
am neq 0 e
bn neq 0 (isso é: são polinômios de grau
m e
n, respectivamente). Ressalta-se também que esta regra só se aplica para limites em
pm infty, não valendo para
x p.
No caso
g ) por exemplo:
lim x -infty x^2-2 x+33 x^2+x+1=lim x -infty x^23 x^2=13.
Mesmo assim, é bom saber tratar a mão, pois as mesmas técnicas permitem, combinado com raízes por exemplo, calcular outros limites (veja as questões
k ),
l ) etc… abaixo: o exercício é muito bem feito com relação a isso, pois complica gradualmente as questões, que são para serem resolvidas uma depois da outra, na sequência).
h)
5 x^4-2 x+14 x^4+3 x+2=5 x^4 cdot(1-2x^3+1x^4)4 x^4 cdot(1+3x^3+2x^4) undersetx +inftylongrightarrow 54Ou, diretamente usando a regra:
lim x +infty 5 x^4-2 x+14 x^4+3 x+2=lim x +infty 5 x^44 x^4=54.
i)
xx^2+3 x+1=xx^2(1+3x+1x^2)=underbrace1x cdot(1+3x+1x^2)x +infty undersetx inftylongrightarrow 0.
Ou, diretamente usando a regra:
lim x +infty xx^2+3 x+1=lim x +infty xx^2=lim x +infty 1x=0.
Observação: Mesmo que ajuda entender, é melhor evitar escrever o seguinte tipo de coisas:
lim x +infty 1x=1+infty=0
pois
+infty não é um número real, e não tem um bom comportamento algébrico (tipo:
0 cdot+infty= ?)
j)
2 x^3+1x^4+2 x+3=2 x^3 cdot(1+12 x^3)x^4 cdot(1+2x^3+3x^4)=2 cdot overbrace(1+12 x^3)^underbracelongrightarrowx -infty ^1 cdot underbrace(1+2x^3+3x^4)x -inftyunderbracexx -infty 1 underbracex -infty 0^-.
Ou, diretamente usando a regra:
lim x -infty 2 x^3+1x^4+2 x+3=lim x -infty 2 x^3x^4=lim x -infty 2x=0^-.
k)
raiz[3]5+underbrace2xx +infty 0=raiz[3]5, onde usamos a continuidade de
raiz[3]y no ponto 5 .
Portanto,
lim x +infty raiz[3]5+2x=raiz[3]5.
l)
raiz[3]xx^2+3=raiz[3]xx^2 cdot(1+3x^2)=raiz[3]1underbracex cdot(1+3x^2)x -infty undersetx -inftylongrightarrow raiz[3]0=0.
Portanto,
lim x -infty raiz[3]xx^2+3=0.
m)
raizx^2+13 x+2=raizx^2(1+1x^2)3 x(1+2x)=raizx^2(1+1x^2)9 x^2(1+2x)^2=raiz1+1x^29(1+2x)^2 undersetx +infty raiz19=13.
Portanto,
lim x +infty raizx^2+13 x+2=13.
n)
raiz[3]x^3+2 x-1raizx^2+x+1=raiz[3]x^3 cdot(1+2x^2-1x^3)raizx^2 cdot(1+1x+1x^2)=x cdot raiz[3]1+2x^2-1x^3|x| cdot raiz1+1x+1x^2 undersetx inftylongrightarrow 1.
Portanto,
lim x +infty raiz[3]x^3+2 x-1raizx^2+x+1=1.
o) Uma primeira tentativa seria:
x-raizx^2+1=x-raizx^2 cdot(1+1x^2) underset(x >= 0)= x-x cdot raiz1+1x^2=underbracexx +infty+infty cdot underbrace(1-raiz1+1x^2)x +infty
mas dá uma indeterminada
(0 cdot+infty). Outra estrategia é aproveitar da igualdade
(a-b)(a+b)=a^2-b^2 para se desfazer da raiz, como segue:
x-raizx^2+1 & =(x-raizx^2+1) cdot x+raizx^2+1x+raizx^2+1 & =(x-raizx^2+1) cdot(x+raizx^2+1)x+raizx^2+1 & =x^2-x^2-1x+raizx^2+1 & =underbrace-1x+raizx^2+1x infty taxx +infty 0
Portanto,
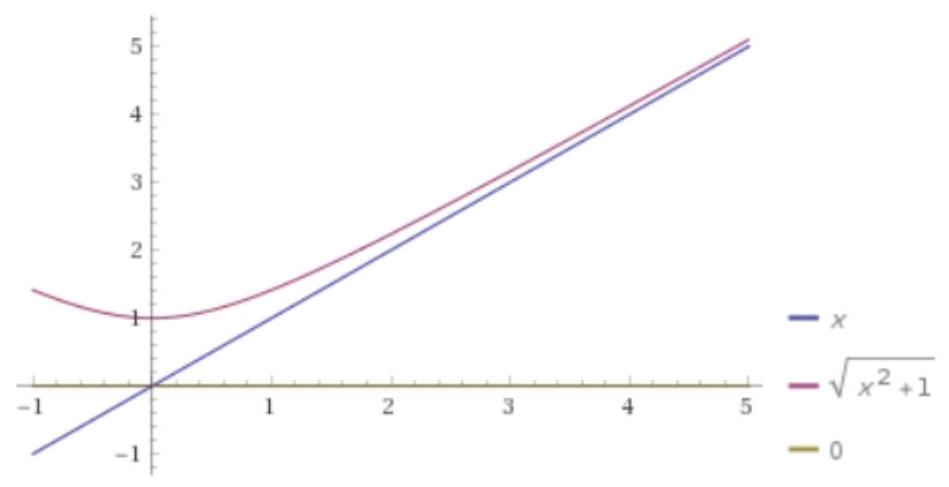
lim x +infty x-raizx^2+1=0.
Comparando ambos gráficos, obtemos:
p) Seguindo a mesma estrategia do que a questão precedente:
raizx+1-raizx+3 & =(raizx+1-raizx+3) cdot raizx+1+raizx+3raizx+1+raizx+3 & =(raizx+1-raizx+3) cdot(raizx+1+raizx+3)raizx+1+raizx+3 & =x+1-x-3raizx+1+raizx+3 & =4raizx+1+raizx+3 undersetx +inftylongrightarrow 0
Portanto,
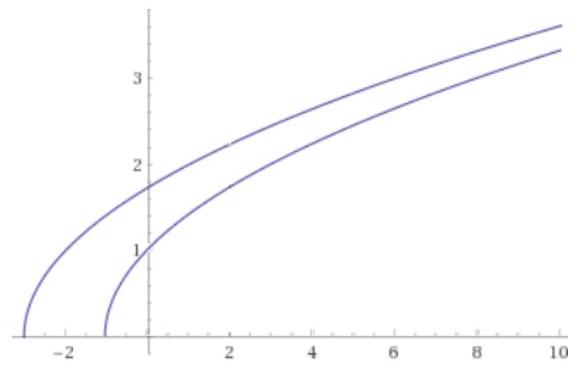
lim x +infty raizx+1-raizx+3=0. Comparando ambos gráficos:
a)
x^4-3 x+2=underbracex^4x +infty+infty cdot underbrace(1-3x^3+2x^4)x +infty undersetx +inftylongrightarrow+infty.
Portanto:
lim x +infty x^4-3 x+2=+infty.
b)
5-4 x+x^2-x^5=underbracex^5x +infty+infty cdot underbrace(5x^5-4x^3+1x^3-1)x +infty undersetx +inftylongrightarrow-infty.
Portanto:
lim x +infty 5-4 x+x^2-x^5=+infty.
c)
3 x^3+2 x+1=underbracex^3x -infty-infty cdot underbrace(3+2x^2+1x^3+1x^3)x -infty undersetx +inftylongrightarrow-inftyPortanto:
lim x -infty 3 x^3+2 x+1=-infty.
d)
lim x +infty x^3-2 x+3=+infty.
e)
lim x +infty 5 x^3-6 x+16 x^3+2=56.
f)
lim x +infty 5 x^3-6 x+16 x^2+x+3=+infty.
g)
lim x +infty 5 x^3+7 x-3x^4-2 x+3=0.
h)
lim x -infty 2 x+3x+1=2.
i)
lim x -infty x^4-2 x+33 x^4+7 x-1=13.
j)
lim x -infty 5-x3+2 x=-12
k)
lim x +infty x+1x^2-2=0.
l)
lim x +infty 2+x3+x^2=0.
Resolução do Ex. 3 [voltar]
a)
raizx+1x+3=raizxx+3+1x+3=raizxx+3+1x+3 underset(x >= 0)= underbrace1raizx+3raizxx +infty+underbrace1x+3x +infty undersetx +inftylongrightarrow 0Outro método:
raizx+1x+3=(raizx+1) cdot(raizx-1)(x+3) cdot(raizx-1) underset(x >= 0)= x-1(x+3) cdot(raizx-1)=underbracex-1x +3substackx +infty x+3 cdot underbrace1raizx-1substacklongrightarrow x +infty undersetx +infty 0
Portanto:
lim x +infty raizx+1x+3=0.
b)
x+raizx+32 x-1=x2 x-1+raizx+32 x-1=underbracex2 x-1substackx +infty 2 x-1+raizunderbracex+3(2 x-1)^2x +infty undersetx +inftylongrightarrow 12+0=12.
Outro método: por mudança de variável, tomando
y:=raizx+3 undersetx +inftylongrightarrow+infty pode-se desfazer facilmente da raiz:
x+raizx+32 x-1=y^2-3+y2(y^2+3)-1=y^2+y-32 y^2+5 undersety +inftylongrightarrow 12
Portanto:
lim x +infty x+raizx+32 x-1=12.
c)
2 x-raizx^2+3 & =2 x-|x| cdot raiz1+3x^2 & =2 x-x cdot raiz1+3x^2=underbracexx +infty+infty (x >= 0) & =underbrace(2-raiz1+3x^2)x +infty undersetx +inftylongrightarrow+infty
Portanto:
lim x +infty 2 x-raizx^2+3=+infty.
d)
x-raiz3 x^2+2 underset(x >= 0)= x-raiz3 x cdot raiz1+23 x^2=underbracexx +infty+underbrace(1-raiz3 raiz1+23 x^2)x +infty undersetx +inftylongrightarrow-infty.
Portanto:
lim x +infty x-raiz3 x^2+2=-infty. Aqui, note que
1-raiz3<0 é negativo !
e)
x-raiz3 x^3+2=x-x^3 / 2 raiz3+2x^3=underbracex^3 / 2+inftyx +infty cdot underbrace(1raizx-raiz3+2x^3)x +infty undersetx +inftylongrightarrow-infty.
Portanto:
lim x +infty x-raiz3 x^3+2=-infty.
f)
x-raizx+3=x-x^2 raiz1+3x^3=x^2 cdot underbrace(1x-raiz1+3x^3)x +infty undersetx +inftylongrightarrow+infty.
Outro método: por mudança de variável
y:=raizx+3 undersetx +inftylongrightarrow+infty, obtemos:
x-raizx+3=y^2-3+y=y^2 cdot(1-3y^2+1y) undersetx +inftylongrightarrow+infty
Portanto:
lim x +infty x-raizx+3=+infty.
g) Aproveitando da identidade
(a+b)(a-b)=a^2-b^2, obtemos:
raizx+raizx-raizx-1 & =(raizx+raizx-raizx-1) cdot(raizx+raizx+raizx-1)raizx+raizx+raizx-1 & =x+raizx-x+1raizx+raizx+raizx-1 & =raizx+1raizx+raizx+raizx-1 & =raizx cdot(1+1raizx)raizx cdot(raiz1+1raizx+raiz1-1x) & =1+1raizxraiz1+1raizx+raiz1-1x undersetx +inftylongrightarrow 12
Portanto:
lim x +infty raizx+raizx-raizx-1=12.
h)
x-raiz[3]2+3 x^3=x-x cdot raiz[3]2x^3+3=x underbrace(1-raiz[3]2x^3+3)x +infty undersetx +inftylongrightarrow undersetx +inftylongrightarrow-infty.
Portanto:
lim x +infty x-raiz[3]2+3 x^3=-infty.
Resolução do Ex. 4 [voltar]
Cuidado com limites do tipo:
1f(x) onde f(x) undersetx plongrightarrow 0
Em geral, um limite não existe (se
f mudar de sinal perto de
x=p, por exemplo).
Caso
f tem sinal constante, positivo ou negativo, perto de
x=p temos:
& f(x) undersetx plongrightarrow 0^+ Rightarrow 1f(x) undersetx plongrightarrow+infty & f(x) undersetx plongrightarrow 0^- Rightarrow 1f(x) undersetx plongrightarrow-infty
Nas duas expressões acima, ainda pode-se trocar
x p por um limite lateral
x p^+ou
x p^-, continuam valendo.
Caso quer calcular um limite do tipo
g(x)f(x), não esqueça de cuidar do sinal de
g também.
a)
5underbrace3-xsubstackx 0^+ x 0^+ undersetx 0^+longrightarrow-infty, portanto:
lim x 3^+ 53-x=-infty.
b)
4underbracex-3substackx 0^- x 3^- undersetx 3^-longrightarrow-infty, portanto:
lim x 3^- 4x-3=-infty.
c)
4underbrace2 x-1substackx 12^+ undersetx 12^+longrightarrow+infty, portanto:
lim x 12^+ 42 x-1=+infty
d)
lim x 0^- 1x=-infty.
e)
2 x+1x=2+1x undersetx 0^+longrightarrow+infty, portanto:
lim x 0^+ 2 x+1x=+infty.
f)
x-3x^2=x(1-3x)x^2=overbraceunderbracelongrightarrowx 0^-^x 0^-1-3x underbracelongrightarrow 1>0x 0^--infty, portanto
lim x 0^- x-3x^2=-infty.
g)
3x^2-x=underbrace3x(x-2)substackx 0^+ x 0^+ undersetx 0^+longrightarrow+infty, portanto:
lim x 0^+ 3x^2-x=+infty.
h)
3x^2-x=underbrace3x(x-2)substacklongrightarrow 0^+ x 0^- undersetx 0^-longrightarrow+infty, portanto:
lim x 0^- 3x^2-x=+infty.
i)
overbraceunderbraceoverbrace3 x+1^x^2-1x 1^+^overbracex 1^++4>0 undersetx 1^+longrightarrow+infty, portanto:
lim x 1^+ 3 x+1x^2-1=+infty.
undersetx 1^-longrightarrow 5>0
j)
overbrace2 x+3underbracesubstackx^2-1 x 1^- undersetx 1^+longrightarrow-infty, portanto:
lim x 1^- 2 x+3x^2-1=-infty.
k)
2 x+3x^2+x=underbraceundersetx 1+2 x+3x(x+1)substackx 0^- x -1^+ undersetx -1^+longrightarrow+infty, portanto:
lim x -1^+ 2 x+3x^2+x=-infty.
Se precisar, faça uma tabela de sinais para ver que
x(x+1) tende a 0 por valores negativas quando
x -1 a esquerda.
l)
x^2-3 xx^2-6 x+9=x(x-3 x)(x-3)^2=xx-3=overbracexunderbracex-3x 3^+ undersetx 3^+longrightarrow+infty, portanto:
lim x 3^+ x^2-3 xx^2-6 x+9=+infty.
undersetx -1+longrightarrow-1<0
m)
2 x+1x^2+x=overbrace2 x+1underbracex(x+1)x -1^+ undersetx -1^+longrightarrow+infty, portanto:
lim x -1^+ 2 x+1x^2+x=+infty.
n)
2 x+1x^2+x=underbracestackrelundersetx(x+1)longrightarrow 1>02 x+1undersetx 0^+overbracex 0^+ undersetx 0^+longrightarrow+infty, portanto:
lim x 0^+ 2 x+1x^2+x=+infty.
o)
3 x-5x^2+3 x-4=underbraceoverbrace3 x-5^longrightarrow-5<0substack^+ 0^+ (x+4)(x-1) undersetx 1^+longrightarrow-infty, portanto:
lim x 1^+ 3 x-5x^2+3 x-4=-infty.
Aqui, se precisar, calcule o Bhaskara para fatorar
x^2+3 x-4=(x+4)(x-1), e faça uma tabela de sinais para ver que tende a 0 por valores positivas quando
x 1^+.
p)
x^2-4x^2-4 x+4=(x+2)(x-2)(x-2)^2=overbrace(x+2)^undersetx 2longrightarrow+4>0underbracex-2x 2^+ undersetx 2^+longrightarrow+infty, portanto:
lim x 2^+ x^2-4x^2-4 x+4=+infty.
q)
3 x^2-41-x^2=(x+2)(x-2)(x-2)^2=underbraceoverbrace3 x^2-4^longrightarrow(1+x)(1-x)undersetx 1^+longrightarrow 0^+ undersetx 2^+longrightarrow-infty, portanto:
lim x -1^+ 3 x^2-41-x^2=-infty.
r)
sen xx^3-x^2=underbracesen xxsubstackx 0^+ longrightarrow cdot underbrace1x(x-1)substackx 0^- x 0^+ undersetx 0^+longrightarrow-infty, portanto:
undersetx 0^+lim sen xx^3-x^2=-infty.
Resolução do Ex. 5 [voltar]
O limite pode ser basicamente qualquer coisa, seguem vários exemplos:
- Tome
f(x)=x e
g(x)=x-7, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)-g(x)=7 é constante, portanto:
- Tome
f(x)=x^2 e
g(x)=x, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)-g(x)=
x(x-1) portanto:
lim x +infty f(x)-g(x)=+infty
- Tome
f(x)=x e
g(x)=x^2, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)-g(x)=
x(1-x) portanto:
lim x +infty f(x)-g(x)=-infty
- Tome
f(x)=x+sin (x) e
g(x)=x, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)-
g(x)=sin (x) portanto:
lim x +infty f(x)-g(x) não existe ã
Resolução do Ex. 6 [voltar]
De novo, um tal limite pode ser qualquer coisa (alem de
-infty ). Seguem vários exemplos:
- Tome
f(x)=x e
g(x)=7 x, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)g(x)=7 é constante, portanto:
- Tome
f(x)=x^2 e
g(x)=x, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)g(x)=x portanto:
lim x +infty f(x)g(x)=+infty
- Tome
f(x)=x e
g(x)=x^2, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)g(x)=1x portanto:
- Tome
f(x)=x sin (x) e
g(x)=x, então
lim x +infty f(x)=+infty e
lim x +infty g(x)=+infty, porem
f(x)g(x)=sin (x) portanto:
lim x +infty f(x)g(x) não existe ã
Resolução do Ex. 7 [voltar] Esboce o gráfico de uma função
f que satisfaça as seguintes condições:
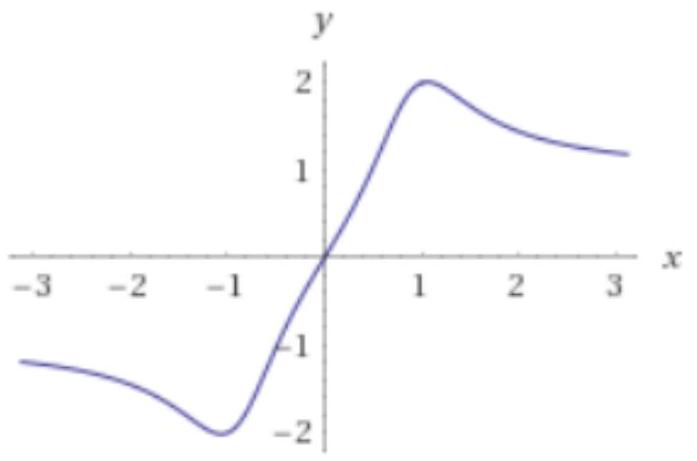
a) Segue o gráfico da função:
f(x)=x^3+(2 raiz2-1) xraizx^6+1
que satisfaz as condições:
f(0)=0, f(1)=2, f(-1)=-2, lim x -infty f(x)=-1 e
lim x +infty f(x)=1.
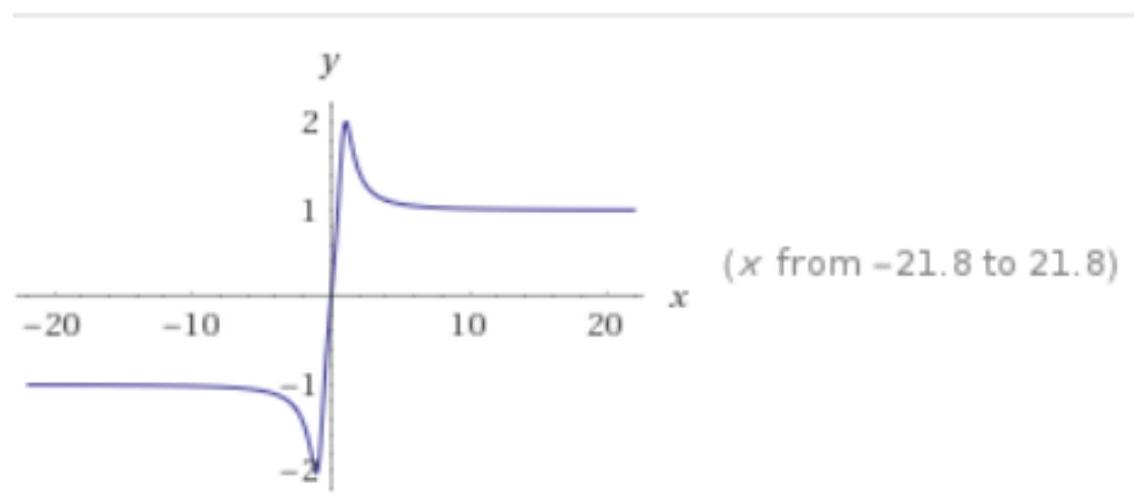
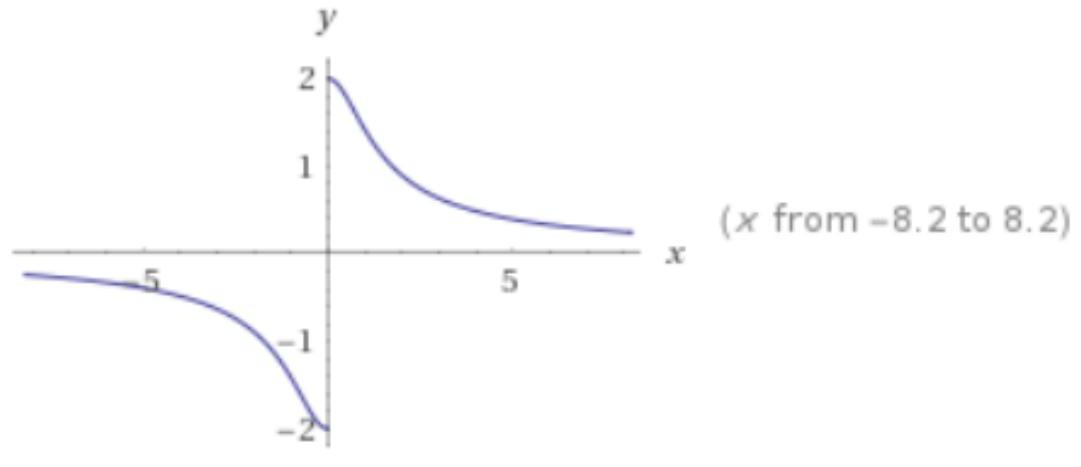
b) Segue o gráfico da função:
que satisfaz as condições:
f(0)=0, lim x -infty f(x)=0, lim x +infty f(x)=0, lim x 0^+ f(x)=2 e
lim x 0^- f(x)=-2.

Resolução do Ex. 8 [voltar]
Temos:
L=L0 cdot underbraceraiz1-1^-substackundersetv c^-underbrace+ v c^- undersetv c^-stackrelv^2c^2 0^+
portanto
lim v c^- L=0. O limite lateral à esquerda foi necessário pois para
v>c, 1-v^2c^2 é negativo, e a raiz
raiz1-v^2c^2 não é definida.)