Equações de Navier-Stokes
Teoria
Fala aí! Seja bem vindo ao Responde Aí! Bora aprender a Equação de Navier-Stokes?!
Qual é a Equação de Navier-Stokes?
Sem enrolação, a equação de Navier-Stokes é essa daqui:
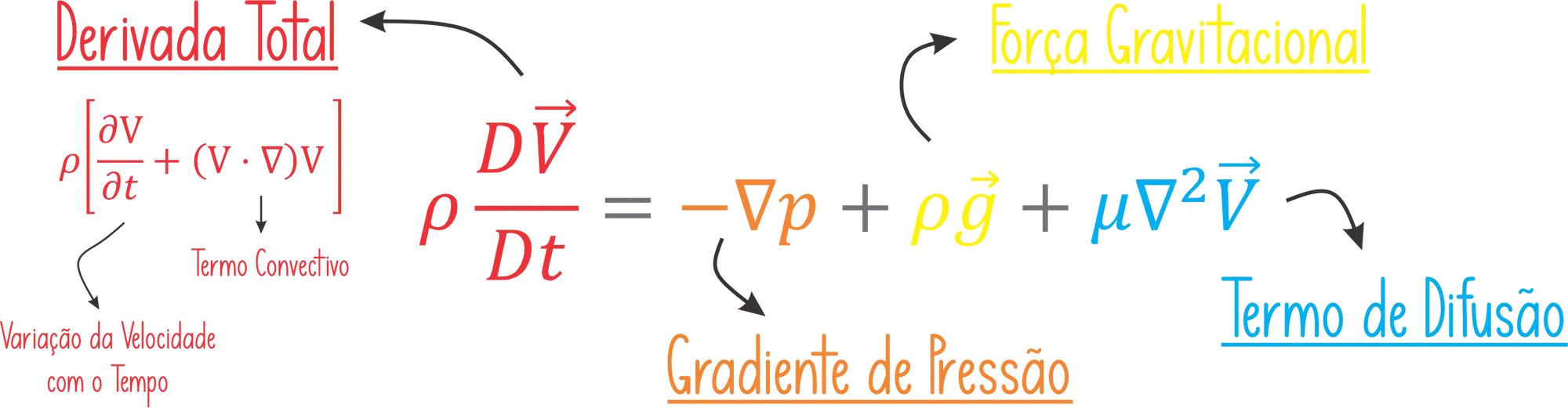
Sim, ela é é assustadora! Mas fica tranquilo, é só uma questão de tempo pra você pegar intimidade! Como falamos lá em cima, a Equação de Navier-Stokes nos descreve o escoamento de um fluido, então nada mais justo do que essa equação levar em conta DIVERSOS fatores, certo?!
Mas fica tranquilo, quando a gente partir pros exercícios você vai ver que é bem comum usarmos hipóteses simplificadas, então a equação fica bem menor e mais simples!
📢 Clique para ver mais:
- Introdução à Mecânica dos Fluidos - FOX: Resolução Completa
- Equação de Navier-Stokes: Exercícios Resolvidos
- Equação da Continuidade
Equação de Navier-Stokes: Coordenadas Retangulares
A equação que vimos lá em cima leva em conta os todos os eixos, que quando estamos falando de coordenadas retangulares são
Mas na prática, na hora dos exercícios a gente precisa abrir essa equação. A versão aberta da equação de Navier-Stokes nas coordenadas retangulares tem essa carinha aqui:
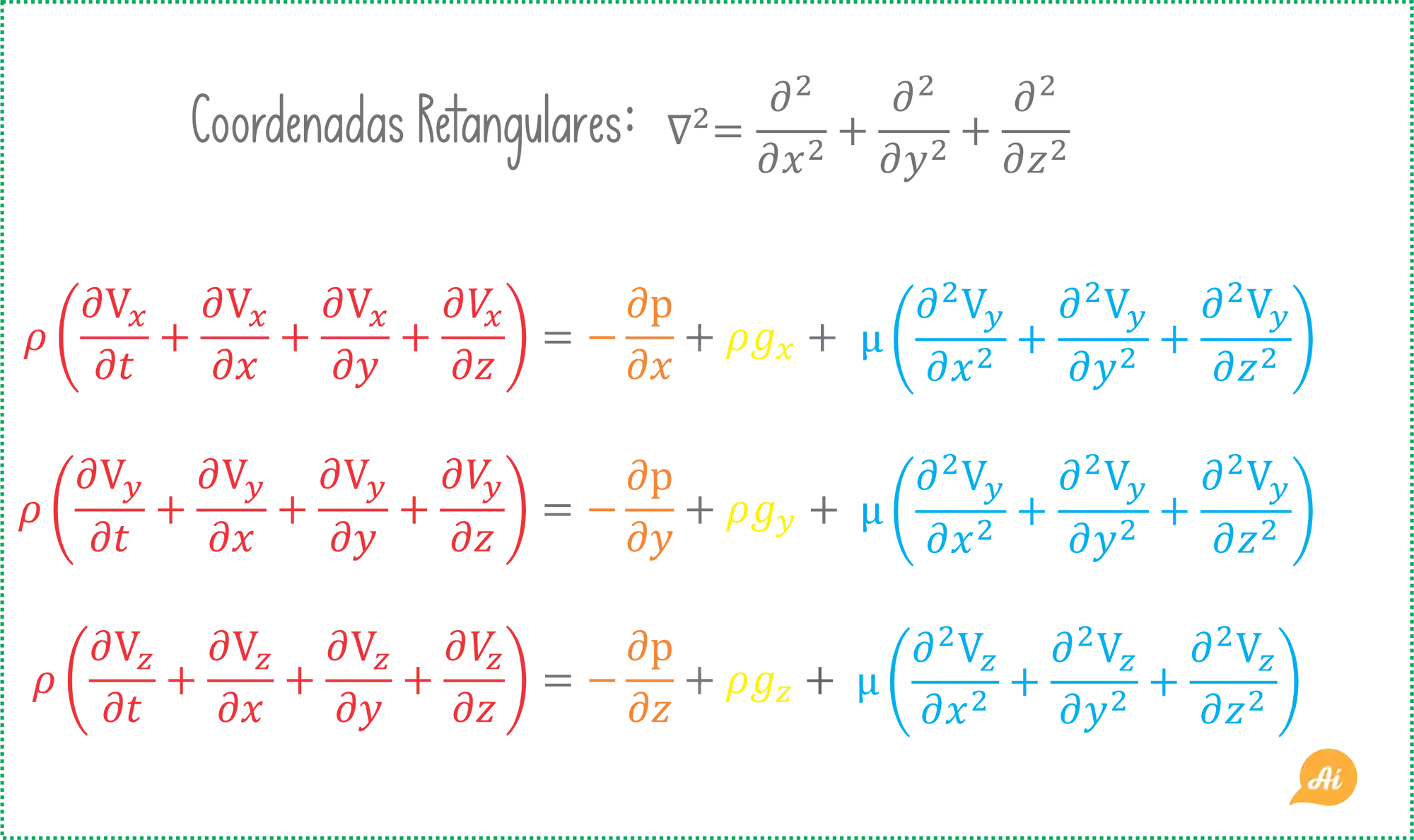
Como você pode ver, estão presente todos os termos que vimos na equação lá do início! Só que aqui você pode lidar com cada eixo de uma forma separada!
-Beleza, mas o que eu quero saber é como eu uso a equação de Navier-Stokes na prática! Como ela vai aparecer nos exercícios!
Seu pedido é uma ordem! Se liga nesse videozinho que o Responde Aí preparou pra você! Nele a gente explica melhor qual é o significado de cada termo da Equação de Navier-Stokes, como usa-la em exercícios e muito mais! 👇 🤩
Equação de Navier-Stokes: Coordenadas Cilíndricas
Quando escolhemos o sistema de coordenadas cilíndricas para o nosso problema, precisamos usar a equação de Navier-Stokes nessa coordenada. Então temos:
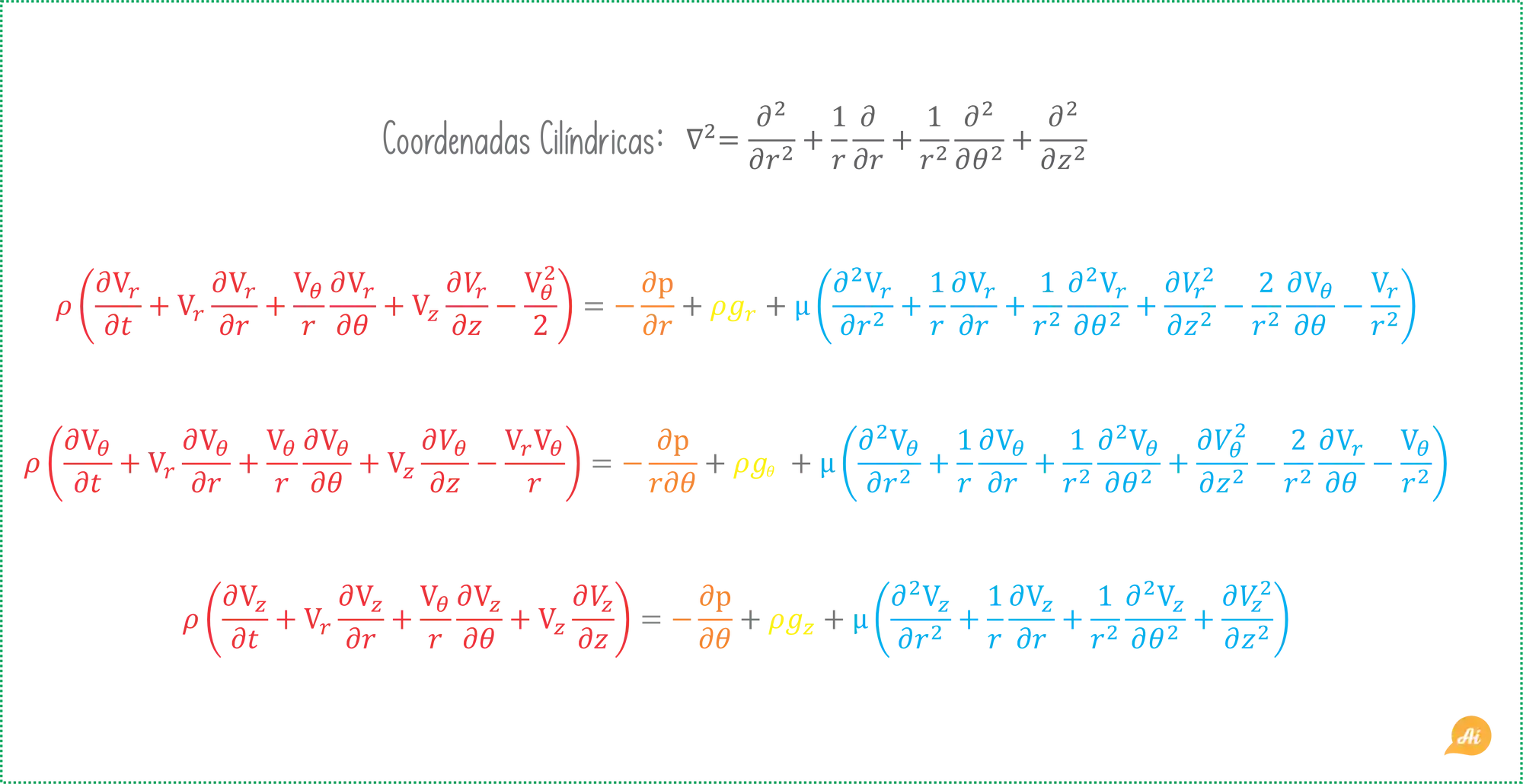
Como usar a Equação de Navier-Stokes
Pra a gente aprender como usar a equação de Navier-Stokes, vamos fazer um exercício juntos!
Considere um escoamento permanente, bidimensional, incompressível, de um fluido newtoniano no qual o campo de velocidade é
Você pode conferir a resolução desse exemplo no vídeo abaixo:
Agora vamos praticar com mais exercícios?!
Como usar a Equação de Navier-Stokes
Exercícios Resolvidos
Exercício Resolvido #1
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 293, ex. 5.38
Considere o campo de velocidade no plano dado por:
Determine o número de dimensões do escoamento, se ele é um possível escoamento incompressível e a aceleração de uma partícula fluida no ponto .
Passo 1
E aí, tudo bem? Tudo vai ficar tranquilo quando analisarmos esse perfil de velocidade! 😊
Separando a velocidade V em , e (suas componentes nos eixos x, y e z respectivamente), temos isso aí:
Repara uma coisa em , e : nenhuma delas depende de z! As componentes da velocidade dependem apenas de x e y. Isso quer dizer que o escoamento está acontecendo justamente no plano xy. Ou seja, é um escoamento bidimensional :D
Então, encontramos a resposta da letra a. O número de dimensões do escoamento é 2.
Passo 2
Para saber se esse escoamento bidimensional é incompressível, precisamos verificar se a Equação da Continuidade é satisfeita.
Equação da Continuidade:
Considerando escoamento permanente e incompressível :
Lembrando que:
Aplicando o campo de velocidade na equação da continuidade:
Logo, o campo de velocidade considerando fluido incompressível satisfaz a continuidade.
Ou seja, é um escoamento incompressível!
Passo 3
Para calcular a aceleração em um ponto, precisamos encontrar a expressão da aceleração e aplicá-la nesse ponto.
Como conseguir essa expressão? A derivada da velocidade é a aceleração, então vamos derivar nosso campo de velocidade
Lembrando que fizemos a hipótese de escoamento permanente no Passo 2, as derivadas em relação ao tempo serão nulas
Além disso, nenhuma componente da velocidade depende de z, então as derivadas em relação a z também são zero
Tá ficando menor, vamos que vamos! 😊
Agora vamos lembrar do campo de velocidade e finalmente derivar
Organizando
O enunciado pede a aceleração no ponto (1, 2, 3), logo:
Logo, a aceleração no ponto (1, 2, 3) é
Resposta
(a)2 dimensões
(b)Sim, é um escoamento incompressível
(c)
Exercício Resolvido #2
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
O escoamento pelo bocal convergente da Figura pode ser aproximado por uma distribuição de velocidades unidimensional
Encontre uma expressão geral para a aceleração do fluido no bocal.
Para o caso específico e , calcule a aceleração, em g’s, na entrada e na saída.
Passo 1
Esse problema exige de nós lembrar que a aceleração de um fluido é a primeira derivada da velocidade.
Como nosso escoamento é unidimensional, nossa expressão da aceleração se reduz a um termo.
Ao invés de analisarmos isso tudo:
É necessário olhar apenas a primeira equação:
Passo 2
Devemos agora substituir a expressão:
Na equação:
Logo, resolvendo cada derivada:
Somando tudo, temos a resposta da Letra A:
Passo 3
Na letra B ele nos pede para substituir e , na expressão que encontramos para a aceleração na entrada e na saída :
Na entrada ():
Na saída ()
Sabendo que:
Resposta
Letra a)
Letra b)
Exercício Resolvido #3
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um campo de velocidade bidimensional é dado por
em unidades arbitrárias. Em , calcule as acelerações e , o componente de velocidade na direção , a direção da velocidade máxima e a direção da aceleração máxima.
Passo 1
Neste exercício, temos um campo bidimensional de velocidade, logo podemos reduzir o númeo de equações de aceleração para duas apenas:
Sabemos que a componente da velocidade no eixo é igual a e que no eixo é igual a , podemos reescrever o campo nos termos de e :
Passo 2
Na letra a, o problema nos pede para calcular e , que nada mais são:
Resolvendo então as derivadas, primeiro para :
Para :
Em :
E, mais rápido dessa vez:
Passo 3
Na letra b, o exercício nos pede a representação de em uma direção .
Isso é nada menos que a projeção de em um vetor que representa essa direção.
Podemos definir um vetor unitário.
Substituindo em :
Realizando o produto escalar
Passo 4
Na letra c, temos que calcular em que direção temos velocidade máxima.
Já sabemos da letra anterior que
Percebe que se seguirmos o mesmo princípio da letra b, devemos achar um ângulo que maximize .
Isso lembra máximo e mínimos de cálculo, e é exatamente o que faremos:
Para arbitrário:
Vamos chamar essa expressão de e derivá-la em :
Para encontrarmos um ponto ótimo devemos igualar a zero:
Temos que lembrar que em um cículo trigonométrico dois ângulos pelo menos tem a mesma tangente, e eles estão separados por .
No nosso problema um deles nos dará a máxima velocidade e outro a mínima, que são iguais em módulo:
E,
Logo é máxima em módulo nestes dois ângulos.
Passo 5
Finalmente, repetiremos o processo do Passo 4, mas agora para a aceleração:
Em calculamos
Sendo
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Exercício Resolvido #4
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um campo de escoamento permanente, incompressível, sem atrito, é dado por
em unidades arbitrárias. Seja a massa específica e despreze a gravidade. Encontre uma expressão para o gradiente de pressão na direçãoo .
Passo 1
Neste exercício ele nos dá algumas infomações bem importantes:
-Escoamento permanente: toda derivada temporal será igual a zero
-Escoamento incompressível: a massa específica é constante em todo escoamento
-Sem atrito: viscosidade desprezível
-Desprezaremos a gravidade
Agora só precisamos saber quem é nosso gradiente de pressão
Passo 2
Aplicando as condições do Passo 1 na primeira expressão de Navier-Stokes:
Ou seja,
O que nos resta é
Sabemos que:
Sendo
Juntando tudo temos a seguinte expressão para resolver:
Passo 3
Do enunciado:
Aplicando na nossa expressão
Resposta
Exercício Resolvido #5
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um campo de escoamento incompressível, tridimensional, proposto tem a seguinte forma vetorial:
Determine se esse campo é uma solução válida para a continuidade e para Navier-Stokes. Se , encontre o campo de pressão .
Passo 1
Neste exercício temos as seguintes informações do enunciado:
-O campo de velocidade :
-Escoamento incompressível:
-Gravidade apenas em :
Passo 2
Letra a e b)
Aplicaremos o campo primeiro a Equação da Continuidade:
Portanto, esse campo satisfaz a continuidade
Aplicando a Navier-Stokes:
Agora separando as varíáveis de cada uma das equações e integrando:
Na segunda equação:
Na terceira:
Podemos dizer por comparação:
Ou,
Resposta
Letra a)É válido para ambos
Letra b)
Exercício Resolvido #6
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Considere um escoamento permanente, bidimensional, incompressível, de um fluido newtoniano no qual o campo de velocidade é conhecido: , , . Esse escoamento satisfaz a conservação da massa? Encontre o campo de pressãose a pressão no pontoé igual a .
Passo 1
Vamos lá,
O enunciado já nos fornece as seguintes informações:
-Escoamento permanente, ou seja, independe do tempo;
-Escoamento incompressível, ou seja, ;
-Fluido newtoniano, ou seja, ;
-O campo de velocidade:
-Na letra A devemos aplicar este campo na Equação da Continuidade;
-Na letra B, aplicar nas equações de Navier-Stokes para encontrarmos o campo de pressão.
Passo 2
Letra a)
A Equação da Continuidade:
Aplicando as informações do enunciado:
Substituindo o campo de velocidade:
Satisfaz portanto a Continuidade.
Passo 3
Letra b)
Utilizaremos as seguintes equações de Navier-Stokes:
Simplificando com as informações do enunciado e que a velocidade não varia em :
Podemos fazer uma suposição de que só exista componente da gravidade no eixo , ou seja que nosso referencial esteja com o eixo paralelo a direção da força de gravidade
Substituindo e nas expressões
Devemos então realizer as integrações parciais:
Resolvendo a primeira:
O mesmo para a segunda:
Comparando as duas expresses podemos dizer que:
Ou que,
Substituindo ou em uma das expressões, podemos encontrara pressão :
Passo 4
Aplicando a condição de Contorno fornecida :
Logo a expressão da pressão é a que segue:
Arrumando um pouco:
Resposta
Letra a)
Sim.
Letra b)
Exercício Resolvido #7
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Considere a esfera de raio imersa em uma corrente uniforme , como mostra a Figura. De acordo com a teoria, a velocidade do fluido ao longo da linha de corrente é dada por
Encontre a posição da aceleração máxima do fluidod ao longo de e o tempo necessário para que uma partícula de fluido se desloque de a .
Passo 1
O enunciado nos fornece o campo de velocidade
e nos pede a aceleração máxima ao longo de , antes então devemos encontrar a função que define essa aceleração.
Passo 2
Sabemos que:
Como é um campo unidimensional,
Se,
Temos que:
Substituindo :
Devemos então encontrar o ponto que é máximo, ou seja,
Passo 3
Na letra b) queremos calcular quanto tempo leva para o fluido se movimentar de até .
Sabemos que
Se separarmos a varíáveis ficamos com,
Integrando nos corretos limites de integração:
Tentar resolver esta integral é muito complicado, pois ela não converge para um valor e tende ao infinito. O objetivo da questão era demonstrar que o fluido leva um tempo infinito para chegar ao ponto de estagnação em , onde a velocidade do fluido é zero.
Logo,
Resposta
Letra a)
Letra b)
Exercício Resolvido #8
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Das equações de Navier-Stokes para escoamento incompressível em coordenadas polares encontre o caso mais geral de movimento puramente circulatório , , para escoamento sem escorregamento entre dois cilindros concêntricos fixos, como na Figura.
Equação da continuidade em coordenadas cilíndricas:
Equações de Navier-Stokes em coordenadas cilíndricas:
Passo 1
Primeiro de tudo já sabemos que só está em função de , e que . Já sabemos daí que a continuidade será satisfeita.
Esses dados simplificarão em muito o problema também. Queremos encontrar o valor da função . Vamos supor que os efeitos gravitacionais não existem.
Passo 2
Da equação de de Navier-Stokes, já aplicando as condições do Passo 1:
Por simetria podemos dizer que não varia com :
Se resolvermos a derivada pela Regra do Produto:
A solução desta equação é:
Passo 3
Se substituirmos as condições de contorno devido ao não escorregamento:
Para também por não-escorregamento:
Supondo que
Se isso for verdade, não haveria escoamento entre os cilindros para satisfazer as condições inciais.
Como o escoamento pode existir, devemos reavliar as hipóteses iniciais. Podemos dizer que o escoamento não existe em estado permanente, ou seja, suas condições variam no tempo o que torna o escoamento muito mais complicado de analisar.
Mas isso não excluiu o fato de existir uma solução geral de escoamentos entre cilindros concêntricos.