Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Equação Diferencial da Continuidade

Ver Todos os Exercícios

Teoria

Opa! Seja muito bem vindo ao Responde Aí! Bora conversar sobre esse carinha super importante na Mecânica dos Fluidos, a Equação Diferencial da Continuidade?!

Equação da Continuidade

Talvez você já tenha ouvido falar em equação da continuidade e inclusive feito exercícios sobre no ensino médio, e ela tinha essa carinha aqui:

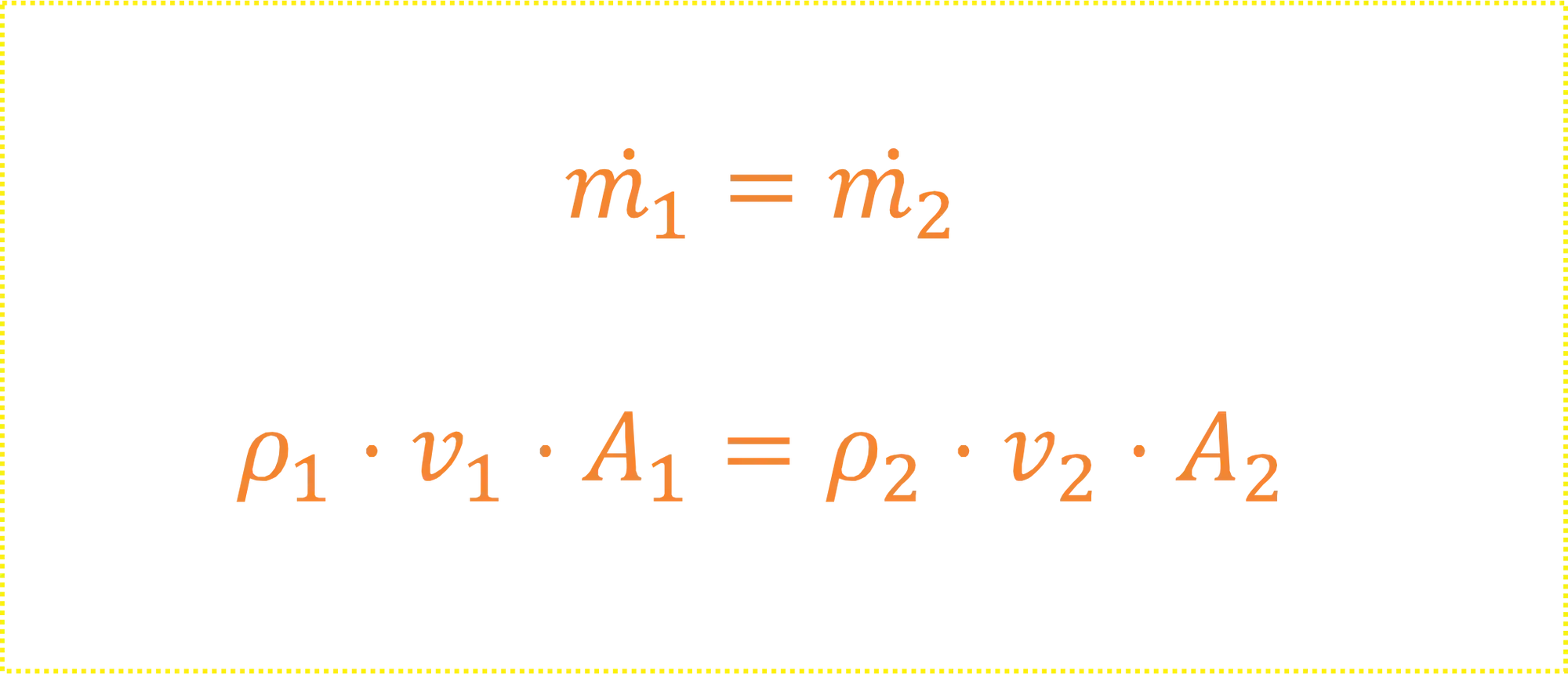
Equação da Continuidade
Equação da Continuidade

Basicamente o que essa equação tá dizendo pra a gente é que a vazão mássica que entra é igual a vazão mássica que sai . Ou seja, temos um regime permanente!

A questão é, essa velocidade é uma velocidade média! O que é ótimo, inclusive super útil, mas as vezes estamos interessados em um perfil de velocidade do escoamento. É ai que entra a forma diferencial da equação de continuidade!

Forma Diferencial da Equação da Continuidade

A equação da continuidade em sua forma diferencial vai ter essa carinha aqui:

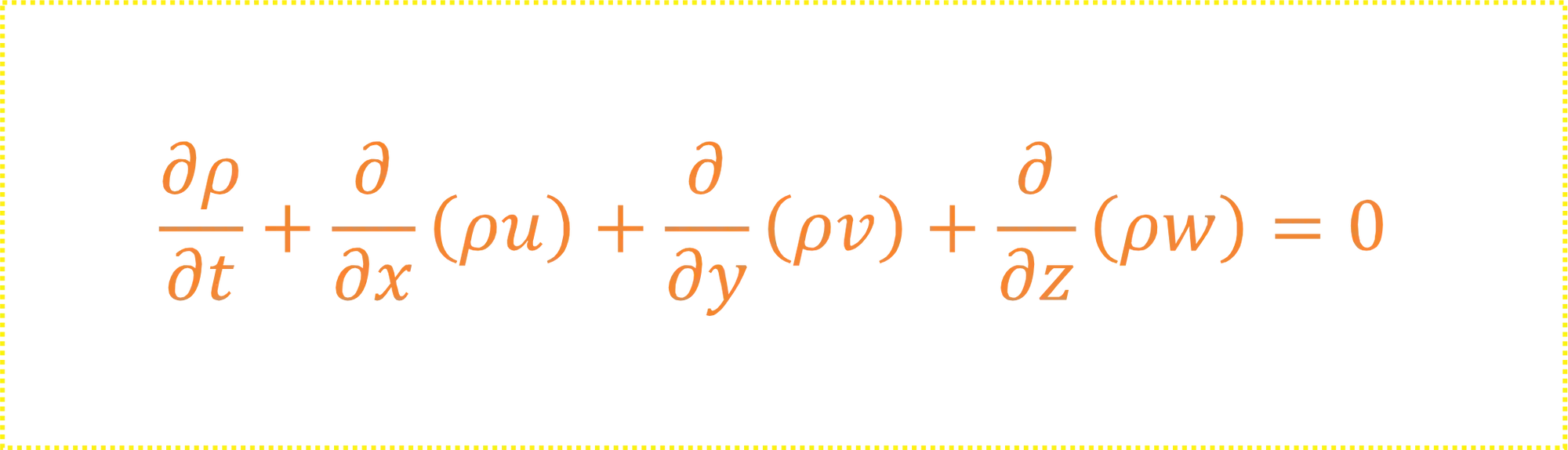
Equação Diferencial da Continuidade.
Equação Diferencial da Continuidade.

Onde:

  • é o termo de acúmulo, que só vamos usar quando o regime for transiente;
  • são as velocidade nos eixos respectivamente;
  • é a densidade do fluido.

Mas calma, não se assusta! Vamos entender o contexto e depois a gente foca na fórmula!

📢 Clique para ver mais:

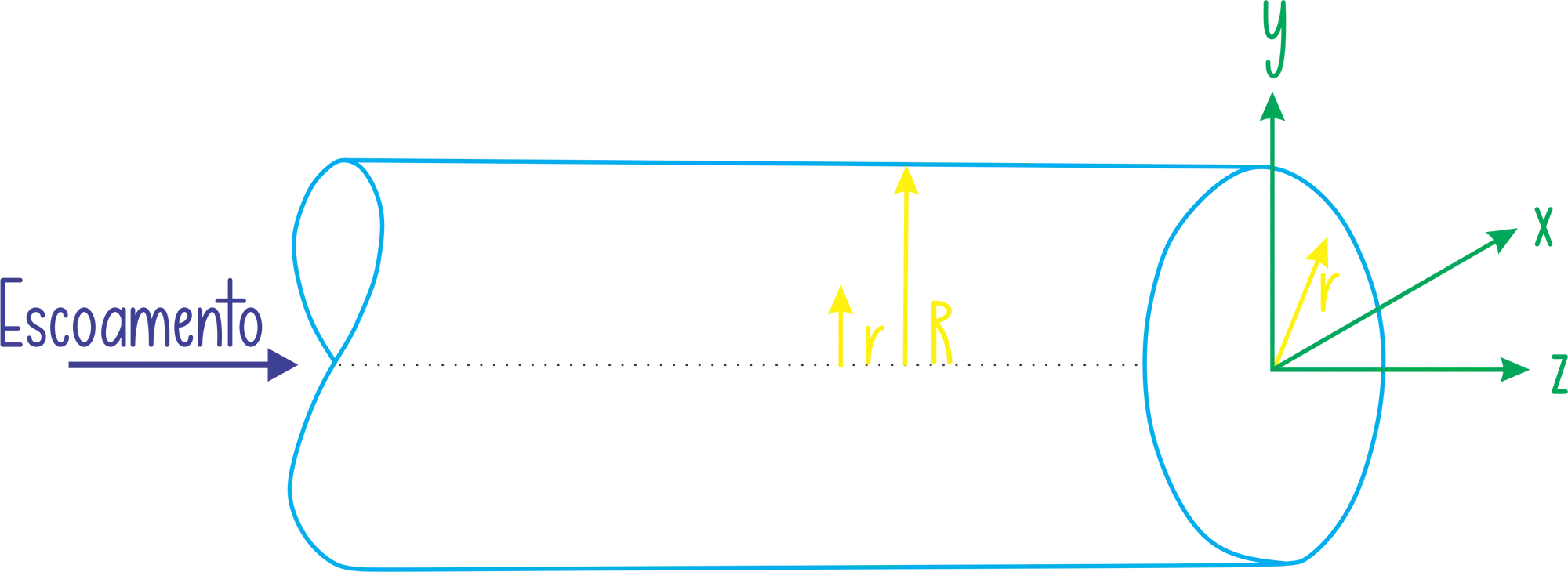
Na figura a baixo temos um escoamento dentro de uma tubulação. Com as informações que temos até agora, para calcular a velocidade na qual o fluido escoa, precisaríamos saber a área do tubo e a vazão mássica do fluido. Assim poderíamos encontrar a velocidade média do fluido!

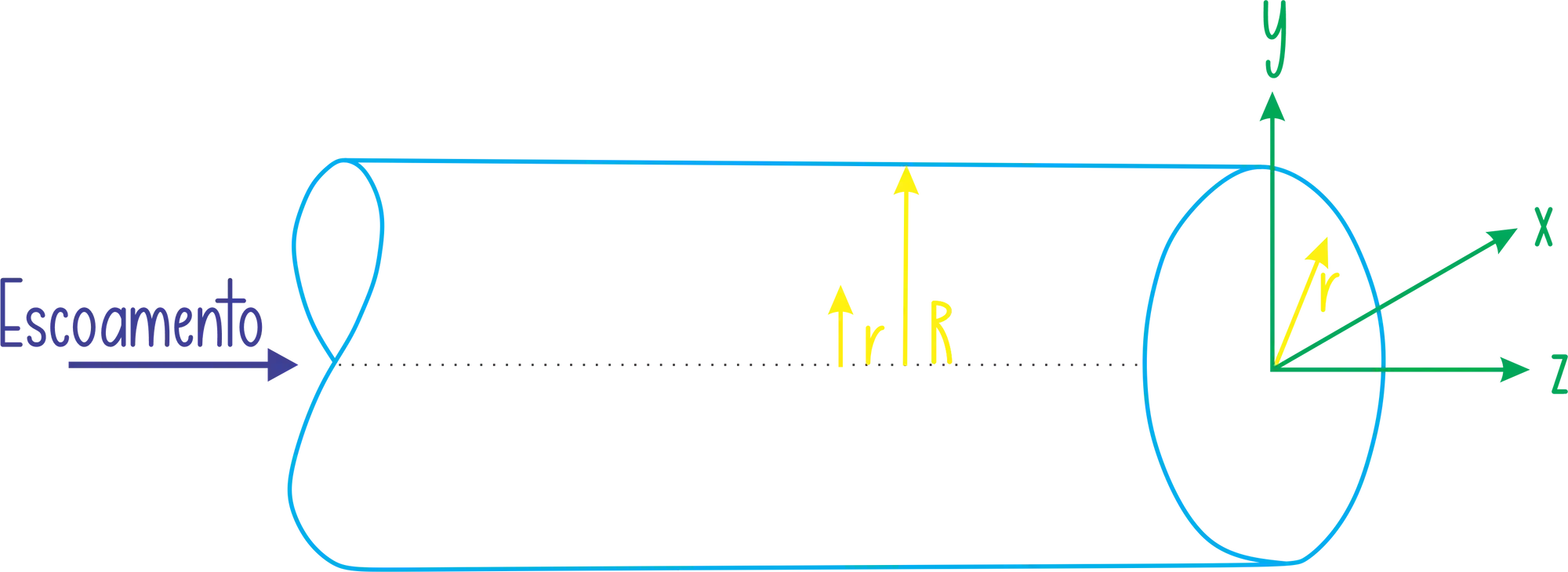
Equação da Continuidade: Escoamento dentro de um tubo
Equação da Continuidade: Escoamento dentro de um tubo

Mas aqui a gente esta interessado em perfil de velocidade, lembra?

Pegando a imagem acima como exemplo e considerando um regime desenvolvido e laminar, teríamos um perfil de velocidade assim:

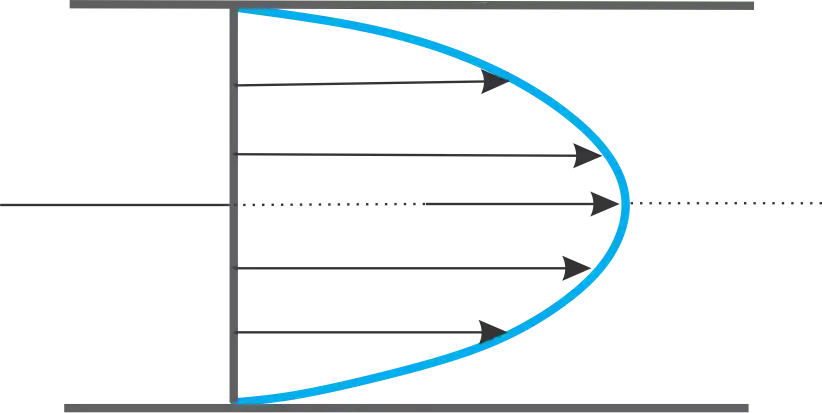
Perfil de velocidade
Perfil de velocidade

Para determinar esse perfil de velocidade, usamos a equação da continuidade na sua forma diferencial!

Beleza, mas na prática…nos exercícios, como eu uso a equação da continuidade na sua forma diferencial?!

Nesse vídeo abaixo a gente explica isso e mais um pouco! 👇 😉

Equação da Continuidade: Coordenadas Cilíndricas

A Equação da continuidade pode ser representada em coordenadas cilíndricas também. Só que nesse caso as componentes de velocidade são (velocidade radial), (velocidade circular) e (velocidade axial).

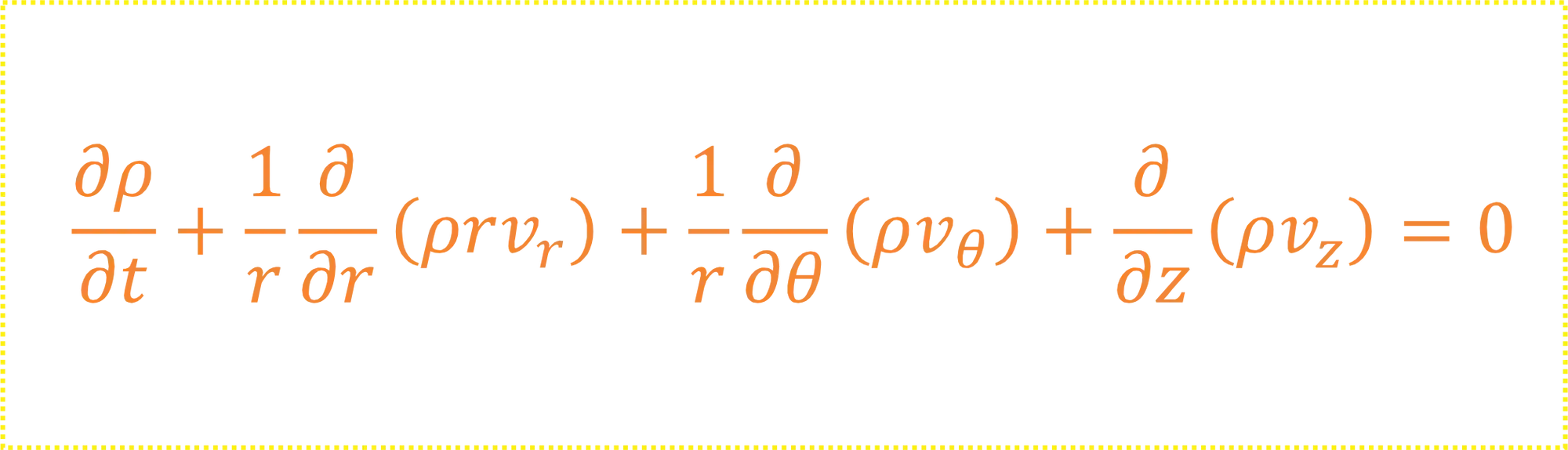
Equação da Continuidade: Coordenadas Cilíndricas
Equação da Continuidade: Coordenadas Cilíndricas

Agora vamos aplicar a equação da continuidade:

Escoamento dentro de um tubo
Escoamento dentro de um tubo

Vamos assumir um escoamento permanente, logo de cara já riscamos o termo de acúmulo . Como já falamos o escoamento tem velocidade na direção do eixo , então também podemos cortar as derivadas com velocidade angular e radial .

Dessa forma ficamos com a seguinte expressão:

Considerando que a densidade se mantém constante ao longo do escoamento:

E qual a interpretação física que podemos tirar disso?

A derivada de uma constante vai ser sempre igual a zero. Logo é constante e podemos dizer que ao longo do eixo a velocidade não muda!

-Mas quando teríamos velocidade angular ou radial ?

Para velocidade angular podemos imaginar uma máquina de lavar roupa, cheia de água no momento que ela esta centrifugando! Agora para velocidade radial imagina que você pegou uma mangueira de água tapou sua extremidade, onde a água sai e fez vários furinhos no cano! Quando você ligar a torneira a água vai esguichar no sentido radial!

Equação da Continuidade: Forma Vetorial

Podemos escrever nossas equações da seguinte maneira também, que é um pouco mais fácil de memorizar:

Sendo . Esse delta invertido é o que a gente chama de nabla, e no caso ele calcula o divergente do campo de velocidades. Isso nada mais é do que a derivada parcial de determinado termo nas direções do eixo de referência utilizado.

Agora vamos praticar com exercícios?

Equação da Continuidade: Coordenadas Cilíndricas

Equação da Continuidade: Forma Vetorial

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria.

Um caso muito comum na mecânica dos fluidos é o caso permanente e incompressível.

Deduza a expressão da Equação da Continuidade para o caso permanente, ou seja, sem variações no tempo, e incompressível, onde ρ é constante.

Passo 1

Temos a equação da continuidade:

∂ ρ ∂ t + ∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z = 0

Aplicando a primeira condição de escoamento permanente

∂ f ∂ t = 0

Senfo f uma função qualquer

∂ ρ ∂ t = 0

Logo

0 + ∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z = 0

Passo 2

Se ρ é constante, podemos tirar de dentro das derivadas:

ρ ∂ u ∂ x + ρ ∂ v ∂ y + ρ ∂ w ∂ z = 0

Colocando ρ em evidência

ρ ∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Como ρ é diferente de zero, podemos jogar ele pro outro lado da equação

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0 ρ = 0

Logo a expressão procurada é:

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Esta expressão será bastante usada daqui pra frente nos exercícios.

Resposta

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Exercício Resolvido #2

Elaboração própria

Considere o seguinte campo de velocidade bidimensional para um escoamento permanente e incompressível:

V = x 2 y i -   x y 2 j

Essa distribuição de velocidade satisfaz a equação da continuidade? Esse escoamento é possível?

Passo 1

Bem, na teoria, vimos que a equação da continuidade aqui na Análise Diferencial é essa aqui:

∂ ρ ∂ t + ∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

E como o enunciado diz que o escoamento é permanente, a derivada em relação ao tempo é zero ∂ ρ ∂ t = 0 . Logo, a equação da continuidade fica assim:

∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

Além disso, o fluido é incompressível, o que nos permite colocar a massa específica para fora da derivada, pois ela é constante e independe de x, y e z.

ρ ∂ u ∂ x + ρ ∂ v ∂ y + ρ ∂ w ∂ z = 0

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Com essa equação, vamos analisar agora o perfil de velocidades!

Passo 2

Quem são u , v , e w ?

Essas letras são as componentes da velocidade em cada direção. Lembrando que o perfil de velocidade foi dado no enunciado:

V = x 2 y i -   x y 2 j

Podemos escrever em termos de cada componente:

  u = V x =   x 2 y

v = V y =   - x y 2

Como o escoamento é bidimensional:

w = V z = 0

Substituindo na equação da continuidade para regime permanente e fluido incompressível:

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

∂ ( x 2 y ) ∂ x + ∂ ( - x y 2 ) ∂ y + 0 = 0

Resolvendo as derivadas parciais 2 x y - 2 x y + 0 = 0

0 = 0

Então, para a distribuição de velocidades dada, a equação da continuidade é satisfeita! Ou seja, esse escoamento é possível.

Resposta

Sim, a distribuição de velocidades dada satisfaz a continuidade.

Sim, o escoamento é possível.

Exercício Resolvido #3

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Um escoamento idealizado incompressível tem a distribuição tridimensional de velocidade proposta:

V = 4 x y 2 i +   f y j - z y ² k  

Encontre a forma apropriada da função f ( y )   que satisfaz a relação da continuidade

Passo 1

Então galera, vamos antes de tudo lembrar que u , v , e w são as componentes de V em cada direção x , y e z . Ou seja podemos reescrever o campo de velocidade V desse jeito:

u = 4 x y 2

v = f y

w = - z y 2

Nosso objetivo nesse problema é aplicar a Equação da Continuidade e procurar o formato que f ( y ) deve ter.

Passo 2

No enunciado ele nos dá uma informação também muito importante: o escoamento é INCOMPRESSÍVEL. Isso significa sempre que ρ é uma constante, logo qualquer derivada de ρ é igual a zero.

∂ ρ ∂ t + ∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

0 + ∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

Colocando ρ em evidência:

ρ ∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Sabendo que ρ = c o n s t a n t e ≠ 0 dividimos os dois lados por ρ :

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Passo 3

Agora precisamos encontrar os valores de ∂ u ∂ x e ∂ w ∂ z :

∂ u ∂ x = ∂ ∂ x 4 x y 2 = 4 y ²

∂ w ∂ z = ∂ ∂ z - z y 2 = - y ²

Substituindo na expressão da Continuidade:

4 y ² + ∂ v ∂ y - y ² = 0

∂ v ∂ y = - 4 y 2 + y ²

∂ v ∂ y = - 3 y ²

Sabemos que v = f ( y ) , ou seja não depende de nenhuma outra varíavel além de y , podemos reescrever a derivada e realizar a integração:

d v d y = - 3 y ²

d v = - 3 y 2   d y

∫ d v = ∫ - 3 y 2 d y

v = - 3   y 3 3 + C

Logo:

v = f y = - y 3 + C

Sendo C a constante de integraçã.

Resposta

f y = - y 3 + C

Exercício Resolvido #4

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Um campo de velocidade bidimensional é dado por

u = - K y x 2 + y 2

v =   K x x 2 + y 2

Em que K é constante. Esse campo satisfaz a continuidade incompressível? Transforme essas velocidades em componentes polares v r e v θ . O que esse escoamento pode representar?

Passo 1

O enunciado já nos diz a seguinte informação: “Um campo de velocidade bidimensional”, isso significa que w = 0 , pois não há movimento no eixo z .

Outra informação importante é que ele nos pede para checar se o campo de velocidade satisfaz a continuidade INCOMPRESSÍVEL, ou seja, checar a continuidade para ρ = c o n s t a n t e .

Isso tudo reduz a nossa equação conforme faremos abaixo:

∂ ρ ∂ t + ∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

0 + ∂ ∂ x ρ u + ∂ ∂ y ρ v + 0 = 0

ρ ∂ u ∂ x + ∂ v ∂ y = 0

∂ u ∂ x + ∂ v ∂ y = 0

Passo 2

Próxima etapa é aplicar o campo definido por u e v na nossa equação, ou seja, precisamos derivar u em função de x e v em função de y :

∂ u ∂ x = ∂ ∂ x - K y ( x 2 + y 2 )

Aplicando a Regra do Quociente:

f g ' = g f ' - g ' f g ²

No nosso caso:

g = ( x 2 + y 2 ) e f = - K y

∂ ∂ x - K y ( x 2 + y 2 ) = - K y ( x 2 + y 2 ) ' = x 2 + y 2 . 0 - 2 x . ( - K y ) ( x 2 + y 2 ) ²

Arrumando as coisas:

∂ u ∂ x = 2 K x y ( x 2 + y 2 ) ²

Realizando o mesmo procedimento para ∂ v ∂ y :

∂ v ∂ y = ∂ ∂ y K x ( x 2 + y 2 )

∂ v ∂ y = x 2 + y 2 . 0 - 2 y . K x ( x 2 + y 2 ) ²

∂ v ∂ y = - 2 K x y ( x 2 + y 2 ) ²

Aplicando na Continuidade:

∂ u ∂ x + ∂ v ∂ y = 0

2 K x y ( x 2 + y 2 ) ² - 2 K x y x 2 + y 2 2 = 0

0 = 0

Logo, sim a Continuidade é satisfeita.

Passo 3

Para a próxima parte do problema, devemos transformar nossas coordenadas cartesianas em cilíndricas ou polares:

x = r cos ⁡ θ

y = r s en ⁡ θ

Aplicando em u e v :

u = - K y ( x 2 + y 2 ) = - K r s e n ⁡ θ ( r ² cos ² ⁡ θ + r ² s e n ² ⁡ θ )

Sabendo que cos ² ⁡ θ + sin ² ⁡ θ = 1 :

u = - K r s e n ⁡ θ r ² ( cos 2 ⁡ θ + s e n 2 ⁡ θ ) = - K r s e n ⁡ θ r 2

u = - K r s e n ⁡ θ

Fazendo o mesmo para v :

v = K r cos ⁡ θ

Passo 4

Agora para encontrarmos v r e v θ , devemos usar as seguintes relações de transformação de velocidades cartesianas e polares:

u = v r cos ⁡ θ - v θ s e n ⁡ θ

v = v r s e n ⁡ θ + v θ cos ⁡ θ

Comparando com as expressões que encontramos no Passo 3

v r cos ⁡ θ - v θ s e n ⁡ θ = - K r s e n ⁡ θ

É o mesmo que dizer:

v r cos ⁡ θ - v θ sin ⁡ θ = 0 . cos ⁡ θ - K r s e n ⁡ θ

Logo

v r = 0

v θ = K r

E isso representa um vortex potencial.

Resposta

v r = 0

v θ = K r

Representa um vortex potencial.

Exercício Resolvido #5

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Um campo de escoamento incompressível tem os componentes cilíndricos v θ = C r , v z = K R 2 - r 2 , v r = 0 , em que C e K são constantes e r ≤ R , z ≤ L . Esse escoamento satisfaz a continuidade? O que ele pode representar fisicamente?

Passo 1

De novo um escoamento incompressível, logo ρ = c o n s t a n t e .

E mais uma vez aplicaremos o campo de velocidade a Equação da Continuidade, dessa vez na sua forma polar.

Passo 2

Sabemos pelo enunciado que:

v r = 0

v θ = C r

v z = K ( R 2 - r 2 )

Aplicando na Equação da Continuidade:

∂ ρ ∂ t + 1 r ∂ ∂ r ρ r v r + 1 r ∂ ∂ θ ρ v θ + ∂ ∂ z ρ v z = 0

Sabemos também que

∂ ρ ∂ t = 0

O que reduz a nossa equação aos seguintes termos, já dividindo a equação por ρ = c o n s t a n t e

1 r ∂ ( r v r ) ∂ r + 1 r ∂ v θ ∂ θ + ∂ v z ∂ z = 0

Passo 3

Agora só nos resta realizer as derivações

∂ ( r v r ) ∂ r = ∂ ( r × 0 ) ∂ r = 0

∂ v θ ∂ θ = ∂ ( C r ) ∂ θ = 0

∂ v z ∂ z = ∂ ∂ z K R 2 - r 2 = 0

Substituindo na equação:

1 r × 0 + 1 r × 0 + 0 = 0

0 = 0

Passo 4

Esse escoamento pode representa um escoamento circular dentro de um tubo cilíndrico de raio R e altura L que está em movimento circular.

No centro do cilindro o fluido não rotaciona ( v θ 0 = 0 ), apenas move-se no sentido z , com velocidade v z ( 0 ) = K R ² . Na parede do cilindro v z ( R ) = 0 e v θ ( R ) = C R , adiante veremos que isso tem o nome de hipótese do não escorregamento na parede e podemos concluir que o cilindro está rotacionando com velocidade C R .

Resposta

Esse escoamento pode representa um escoamento circular dentro de um tubo cilíndrico de raio R e altura L que está em movimento circular.

Exercício Resolvido #6

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

As coordenadas polares esféricas (r, θ, ϕ) são definidas na figura. As transformações cartesianas são

x = r   s e n   θ cos ⁡ ϕ

y = r   s e n   θ sen ⁡ ϕ

z = r   c o s   θ

A relação da continuidade cartesiana incompressível (Equação 1) pode ser transformada na forma polar esférica (Equação 2)

Equação 1

∂ u ∂ x +   ∂ v ∂ y +   ∂ w ∂ z = 0

Equação 2

1 r 2 ∂ ∂ r r 2 v r + 1 r s e n θ ∂ ∂ θ v θ s e n   θ +   1 r s e n θ ∂ ∂ ϕ v ϕ = 0  

Qual é a forma mais geral de v r quando o escoamento é puramente radial, isto é v θ e v ϕ são nulas?

Passo 1

Então chefe, de cara o exercício nos pede pra encontrar v r sabendo que v θ e v φ são iguais a zero.

Aplicando isso na equação da continuidade que ele nos fornece, sumimos com um monte de termos e ficamos com a seguinte expressão:

1 r 2 ∂ ∂ r r 2 v r = 0

Onde chegamos na seguinte conclusão

∂ ∂ r r 2 v r = 0

Se integrarmos a equação acima em r , chegamos na expressão para v r :

v r ( r , θ , φ ) = 1 r 2 C ( θ , φ )

Onde C θ , φ garante a generalidade da solução.

Passo 2

Aplicando a nossa função na equação, sempre teremos a continuidade satisfeita:

1 r 2 ∂ ∂ r r 2 1 r 2 C ( θ , φ ) = 0

1 r 2 ∂ C ( θ , φ ) ∂ r = 0

Como C ( θ , φ ) não depende de r , a derivada será sempre zero.

Resposta

v r ( r , θ , φ ) = 1 r 2 C θ , φ

Exercício Resolvido #7

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Um pistão comprime gás em um cilindro movendo-se a uma velocidade constante V, como na figura:

Admita que a massa específica do gás e a posição do pistão em t = 0 sejam ρ 0 e L 0 , respectivamente. Considere que a velocidade do gás varie linearmente de u = V na face do pistão até u = 0 em x   = L . Se a massa específica do gás varia apenas com o tempo, encontre uma expressão para ρ ( t ) .

Passo 1

Então, no enunciado já são dadas diversas informações que serão úteis para a gente nesse problema:

- As condições iniciais do pistão;

- O fato da velocidade variar linearmente ( u = a x + b ):

u 0 = V = b

u L = 0 = a L + V

a = - V L

Logo,

u x , t = - V L x + V

Sendo L a posição do pistão que se move com velocidade constante V ,

L = L t = L o - V t

- A massa específica só varia no tempo.

Passo 2

Olhando a equação da continuidade já podemos eliminar algumas derivadas que simplificarão nosso problema:

∂ ρ ∂ t + ∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

d ρ d t + ρ ∂ u ∂ x = 0

Substituindo nossa expressão de u :

d ρ d t + ρ - V L = 0

d ρ d t = ρ V L

Separando as variáveis e integrando:

∫ ρ o ρ d ρ ρ = V ∫ 0 t d t L o - V t

Devemos fazer uma substituição de variáveis x = L o - V t , d x = - V d t

Logo:

d t = - d x V

x 0 = L o

x t = L o - V t

Voltando à equação:

ln ⁡ ρ ρ o = V ∫ L o L o - V t - 1 x d x V

ln ⁡ ρ ρ o = - ∫ L o L o - V t d x x

ln ⁡ ρ ρ o = - ln ⁡ L o - V t L o

ln ⁡ ρ ρ o = ln ⁡ L o L o - V t

Ou:

ρ t = ρ o L o L o - V t

Resposta

ρ t = ρ o L o L o - V t

Exercício Resolvido #8

Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.

Uma aproximação razoável para a camada-limite laminar incompressível bidimensional sobre a superfície plana da figura é

u = U 2 y δ -   y ² δ ²   p a r a   y   ≤   δ   e m   q u e   δ = C x 1 / 2 ,   C = c o n s t a n t e

( a )   Admitindo uma condição de não escorregamento na parede, encontre uma expressão para o componente de velocidade v x , y para y   ≤   δ .

( b ) Depois encontre o valor máximo de v em x = 1   m , para o caso particular do escoamento de ar, quando U = 3   m / s e δ = 1,1   c m .

Passo 1

Do enunciado tiramos as seguintes informações:

u = U 2 y δ - y 2 δ 2 ,   δ = C x 1 / 2

Por curiosidade, condição de não-escorregamento quer dizer que a velocidade do fluido na parede é a mesma da parede, no caso V = 0 .

Passo 2

Pare encontramos v ( x , y ) devemos aplicar a equação da continuidade, para escoamentos incompressíveis e bidimensionais:

∂ u ∂ x + ∂ v ∂ y = 0

Substituindo δ em u :

u = U 2 y C x 1 / 2 - y 2 C x 1 / 2 2

u = U 2 y C x 1 / 2 - y 2 C ² x

Calculando a derivada em x :

∂ u ∂ x = ∂ ∂ x U 2 y C x 1 / 2 - y 2 C 2 x

∂ u ∂ x = U - 1 2 2 y C 1 x 3 / 2 + y 2 C 2 x ²

∂ u ∂ x = U - y C x 3 / 2 + y 2 C 2 x ²

Substituindo na continuidade:

U - y C x 3 / 2 + y 2 C 2 x ² + ∂ v ∂ y = 0

Logo,

∂ v ∂ y = - U - y C x 3 / 2 + y 2 C 2 x ²

Separando as variáveis e integrando:

v = ∫ - U - y C x 3 / 2 + y 2 C 2 x ² d y

v = U ∫ y C x 3 / 2 - y 2 C 2 x ² d y

v = U ∫ y C x 3 / 2 - ∫ y 2 C 2 x ² d y

Logo a resposta da letra a)

v = U 1 2 y ² C x 3 / 2 - 1 3 y 3 C 2 x ²

Passo 3

Se queremos descobrir o valor máximo de v em x = 1   m , devemos usar a relação, para maximizar o valor de v ,

∂ v ∂ y x = 1 = 0

Sabemos que:

∂ v ∂ y = U y C x 3 / 2 - y 2 C 2 x ²

Conhecemos U = 3 m / s , x = 1 e que δ = 1,1   c m = 1,1 ∙ 10 - 2   m

De x   e δ calculamos C :

δ = C x 1 / 2

C = δ x 1 / 2

C = 1,1 ∙ 10 - 2 1

C = 1,1 ∙ 10 - 2

Substituindo em ∂ v ∂ y = 0 ,

0 = 3 y 1,1 ∙ 10 - 2 ∙ 1 3 / 2 - y 2 1,1 ∙ 10 - 2 2 ∙ 1 ²

0 = y 1,1 ∙ 10 - 2 - y 2 1,1 ∙ 10 - 2 2

0 = 1,1 ∙ 10 - 2 y - y ²

y ( 1,1 ∙ 10 - 2 - y ) = 0

Temos duas soluções,

y = 0

Que é onde temos velocidade mínima, na parede.

E,

y = 1,1 ∙ 10 - 2   m = δ

Que é no topo da camada limite

Logo v máximo:

v = U 1 2 y ² C x 3 / 2 - 1 3 y 3 C 2 x ²

v = 3 1 2 0,011 ² 0,011 1 3 / 2 - 1 3 0,011 3 0,011 2 1 ²

v = 3 1 2 0,011 - 1 3 0,011

v = 3 0,033 - 0,022 6

v = 0,0055   m / s

Resposta

Letra a) v = U 1 2 y ² C x 3 / 2 - 1 3 y 3 C 2 x ²

Letra b)

v = 0,0055   m / s

Exercícios de Livros Relacionados

Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação parabólica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,
Um campo de escoamento incompressível tem os componentes cilíndricos v θ = C r , v z = K R 2 - r 2 , v r = 0 , em que C e K são constantes e r ≤ R , z ≤ L . Esse escoamento satisfaz a continuidade? O
Dada as componentes das velocidades de dois escoamentos de fluidos incompressíveis: A )v x = x 2 - yv y = x 3 - 2 x y B ) v x = y 3 - 3 x 2 y v y = 3 x y 2 - x 3 Verificar se os dois escoamentos são p
Sendo v x = x 2 + z 2 + 5 ; v y = y 2 + z 2 , determinar a forma mais simples da componente v z que satisfaça a equação da continuidade para um fluido incompressível.
O movimento de fluido incompressível de peso desprezível realiza-se segundo o campo de velocidades v x = a x ; v y = b y ; v z = c z Determinar as condições para as quais o movimento é possívelVerific