Escoamento em Dutos Circulares
Teoria
Introdução
A partir de agora vamos passar a trabalhar com escoamentos no interior de dutos. E, como o próprio nome sugere, aqui vamos nos preocupar somente com os dutos circulares, beleza?!
Então vamos trabalhar na seguinte situação:
Em um tubo circular de diâmetro e comprimento , escoa óleo de motor, com o objetivo de aquece-lo. A temperatura superficial do tubo é mantida em . A vazão de escoamento e a temperatura do óleo na entrada do tubo são, respectivamente, e .
O que queremos responder é: qual será a taxa de transferência de calor total no tubo?
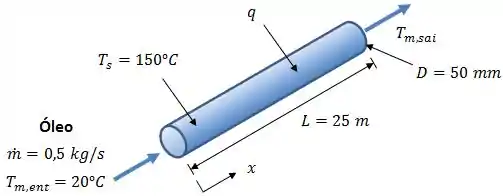
Bom, a taxa de transferência de calor será dada por:
Onde são, respectivamente, vazão mássica, calor específico, temperatura de saída e temperatura de entrada do óleo.
Agora temos dois problemas! O primeiro é que não temos a temperatura de saída do óleo para substituir na fórmula. O segundo é que também não temos o calor específico do óleo ().
E como a gente encontra o ?
Bem, para isso consultamos uma tabela onde podemos achar, não só o valor de , como outras propriedades do fluido. Essas propriedades estão em função da temperatura de referência, que é dada pela seguinte fórmula:
Para calcularmos a temperatura de referência também vamos precisar da ! E agora, o que faremos!!?
Nesse caso, a gente “chuta” uma temperatura de saída . No final das contas, se a temperatura que encontrarmos for bem diferente da que nós chutamos, vamos ter que refazer os cálculos utilizando a temperatura que encontramos... (sim, não tem muito o que fazer em relação a isso).
No nosso caso, como a temperatura de entrada é e a temperatura da superfície é de , podemos chutar uma temperatura de saída , de forma que:
De acordo com a tabela A.5 do Incropera, para as propriedades de óleo de motor a essa temperatura, temos:
Para analisarmos o nosso problema de uma forma coerente, precisamos ter em mente qual as simplificações ou hipóteses podemos assumir no nosso problema! Sabendo disso vamos olhar as condição térmica da superfície do tubo e vamos escolher a que melhor se encaixa! Depois disso seremos capazes de calcular a temperatura de saída do óleo.
Condição Térmica na Superfície do Tubo
Basicamente, temos duas condições:
- Fluxo Térmico na Superfície Constante;
- Temperatura Superficial Constante.
Caso o fluxo térmico seja constante na superfície , a temperatura média a uma distância da entrada no tubo será dada por:
Onde corresponde ao perímetro da superfície.
Agora, se a temperatura superficial for constante, a temperatura média a uma distância da entrada no tubo será dada por:
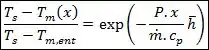
Como este é justamente o caso com o qual estamos trabalhando no nosso exemplo, a temperatura na saída do tubo será dada para , logo:
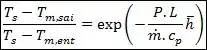
A questão é que agora precisamos do coeficiente convectivo médio , e a questão não nos da esse dado! Para encontra-lo precisamos recorrer as correlações para o número de Nusselt .
Correlações para Escoamento em Dutos Circulares
A relação entre o número de Nusselt e o coeficiente convectivo é dada por:
Onde , , e , são respectivamente, o coeficiente médio de convecção, o número de Nusselt médio, a condutividade térmica do fluido e o diâmetro do duto .
Vou te colocar de cara pro gol aqui, ok? A tabela abaixo mostra todas as correlações para o número de Nusselt que vamos usar nesse tipo de problemas, bem como os requisitos para aplicarmos cada uma delas.
Na coluna dos requisitos temos dois aspectos que vale a pena dar uma atenção, que são:
- Como vamos calcular o número de Reynolds para determinar se o escoamento é laminar ou turbulento;
- Agora temos que saber se o escoamento está plenamente desenvolvido, ou não.
Vamos começar dando uma atenção para o número de Reynolds .
Olha eu aqui de novo! \o/
O número de Reynolds para escoamento interno é dado por:
No entanto, na maioria dos casos, como no nosso problema aqui, nós vamos calcular o número de Reynolds a partir da vazão mássica, dada por:
Isolando :
Sabendo que:
Substituimos essas informações a expressão do número de Reynolds, e encontramos o seguinte:
Assim como acontece para escoamentos em placa plana, por exemplo, temos um valor mágico para o número de Reynolds a partir do qual o escoamento é turbulento. O número de Reynolds crítico vale:
Se substituirmos os valores que temos até agora, teremos o seguinte:
Opa!. Isso significa que o nosso escoamento é laminar!
Agora só nos resta saber determinar o desenvolvimento do escoamento.
“Mas que diabéisso?!”
Desenvolvimento do escoamento
A ideia aqui é basicamente a seguinte. Assim que o fluido entra no tubo, a camada-limite térmica começa a se desenvolver, até que ela se encontra totalmente desenvolvida a partir de uma determinada distância da seção de entrada no tubo.
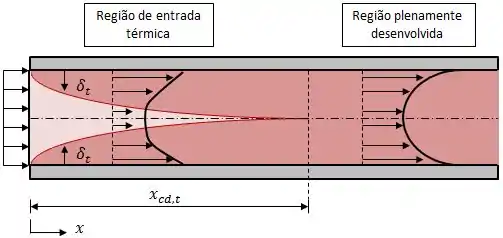
Sendo assim, quando trabalhamos com escoamento interno, precisamos avaliar se a camada-limite térmica está totalmente desenvolvida, ou ainda se desenvolvendo, na região que estamos interessados.
Para o escoamento laminar o comprimento de entrada térmico é dado por:
Para o escoamento turbulento, todas as correlações partem do princípio que o escoamento está plenamente desenvolvido. Então essa é uma preocupação que teremos, basicamente, quando o escoamento for laminar.
Voltando ao nosso problema
Como estamos no regime laminar, precisamos avaliar o desenvolvimento da camada limite.
Substituindo os valores, teremos:
Como o tubo tem somente de comprimento, o escoamento se encontra na região de entrada térmica.
Consultando tabela das correlações, sabendo que , a correlação mais adequada é a seguinte:
Substituindo os valores, encontraremos .
Dessa forma, o coeficiente convectivo médio será dado por:
Agora podemos finalmente encontrar a temperatura de saída , dada por:
Substituindo os valores e jogando isso tudo na calculadora, vamos encontrar o seguinte:
Pra fechar (juro!), podemos calcular a taxa de transferência de calor, dada por:
Só um detalhe! Viu como a temperatura de saída que encontramos ficou bem diferente da temperatura que chutamos no início do problema?!
Isso significa que a taxa de transferência que achamos não corresponde a realidade. Então o próximo passo deve ser refazer todo esse caminho, agora usando a temperatura que acabamos de encontrar (), dessa forma vamos achar uma taxa de transferência mais próxima da real! Vamos fazer isso no primeiro exercício de fixação, ok?
Então partiu colocar isso em prática.
Condição Térmica na Superfície do Tubo
Correlações para Escoamento em Dutos Circulares
Olha eu aqui de novo! \o/
Desenvolvimento do escoamento
Voltando ao nosso problema
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Óleo de motor é aquecido ao escoar através de um tubo circular com diâmetro e comprimento , cuja superfície é mantida em .
Se a vazão de escoamento e a temperatura do óleo na entrada do tubo forem de e , qual será a temperatura do óleo na saída do tubo ? Qual é a taxa de transferência de calor total no tubo?
Dica: Use como chute a temperatura de saída igual a para encontrar as propriedades do óleo.
Passo 1
Na Teoria, chutamos inicialmente uma temperatura de saída igual a . Depois de todos os cálculos, encontramos uma temperatura de saída de . Como a diferença entre o valor que chutamos e o que encontramos foi muito grande, a boa é refazer os cálculos.
Agora usaremos como chute justamente a temperatura de que encontramos no primeiro cálculo.
Dessa forma, a temperatura de referência será:
De acordo com a tabela A.5 do Incropera, para óleo de motor a essa temperatura, temos que:
Passo 2
A taxa de transferência de calor é dada por:
E a temperatura de saída será dada por:
Pra calcular o coeficiente convectivo, vamos precisar do número de Nusselt:
Então vamos agora atrás desse cara.
Passo 3
Para calcular o número de Nusselt, precisaremos do número de Reynolds, dado por:
Substituindo os valores:
Opa! Estamos no regime laminar.
Agora precisamos ver se o escoamento está totalmente desenvolvido, ou se encontra na região de entrada térmica.
Passo 4
O comprimento de entrada térmico é dado por:
Como o tubo tem somente de comprimento, significa que estamos na região de entrada térmica.
Passo 5
Dado o número de Reynolds, o número de Prandtl e a condição do escoamento (região de entrada térmica), a correlação mais adequada é:
Substituindo os valores:
Dessa forma, o coeficiente convectivo será:
Passo 6
A temperatura de saída do óleo de motor será dada por:
Finalmente, a taxa de transferência de calor será:
Obs.: O valor que encontramos para a temperatura se saída agora ficou bem próximo do valor que chutamos, então não é necessário refazer o problema.
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Água em escoamento através de um tubo com de diâmetro e a uma vazão de deve ser aquecida de a pela manutenção da superfície do tubo a uma temperatura de .
Qual é o comprimento do tubo necessário nessas condições?
Passo 1
O primeiro passo é determinar as propriedades da água à temperatura de referência, que é a média das temperaturas de entrada e saída.
Dessa forma:
De acordo com a tabela A.6 do Incropera, para a água a esta temperatura, temos:
Passo 2
Como já temos todas as temperaturas no sistema e este se trata de um caso onde a temperatura superficial é constante, usaremos essa expressão:
Reorganizando os termos para isolar o comprimento , teremos:
Dessa expressão nós temos praticamente tudo, exceto o coeficiente convectivo. Então vamos atrás dele.
Passo 3
Para calcular o coeficiente convectivo, precisamos começar calculando o número de Reynolds.
O primeiro é dado por:
Ou seja, estamos no regime turbulento. Dessa forma, nem precisamos nos preocupar com a condição do escoamento.
Para este valor de Reynolds e o valor do número de Prandtl , podemos usara seguinte correlação:
Como , . Assim substituindo os valores:
O coeficiente convectivo será, então:
Passo 4
Agora podemos finalmente calcular o comprimento adequado para o duto:
Substituindo os valores:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Água de resfriamento escoa através dos tubos, com paredes delgadas e diâmetros de , de um condensador de valor d’água a uma velocidade de , enquanto uma temperatura superficial de é mantida pela condensação do valor.
A temperatura de entrada da água é de e os tubos têm de comprimento.
Qual é a temperatura de saída da água? Determine as propriedades da água a uma temperatura média estimada de .
O valor estimado para foi razoável? Se não, repita o cálculo usando valores para as propriedades determinados a uma temperatura mais apropriada.
Passo 1
Qual é a temperatura de saída da água? Determine as propriedades da água a uma temperatura média estimada de .
Já que o problema nos deu uma temperatura de referência pra buscar as propriedades da água, nem vamos precisar chutar um valor nesse caso.
De acordo com a tabela A.6 do Incropera, para a água a , teremos:
Passo 2
A temperatura de saída pode ser calculada através da seguinte expressão:
Pra calcular o coeficiente convectivo, vamos precisar do número de Nusselt, dado por:
Então vamos agora atrás dele.
Passo 3
Para o número de Nusselt, precisaremos do número de Reynolds, dado por:
Opa! Estamos no regime turbulento, então nem precisamos determinar se o escoamento na saída do duto está plenamente desenvolvido, ou na região de entrada térmica.
A partir dos valores do número de Reynolds e Prandtl , podemos utilizar a seguinte correlação:
Como , . Assim substituindo os valores:
O coeficiente convectivo será, então:
Passo 4
A temperatura de saída será:
Onde e:
Substituindo os valores:
Passo 5
O valor estimado para foi razoável? Se não, repita o cálculo usando valores para as propriedades determinados a uma temperatura mais apropriada.
A média das temperaturas estimada foi de , já a média das temperaturas de entrada e saída que encontramos foi:
Como a diferença entre as duas temperaturas foi pequena, é correto afirmar que o valor estimado para foi razoável. De qualquer forma, se você quiser tentar refazer os cálculos, você deve encontrar uma temperatura de saída mais ou menos igual a:
Resposta
O valor estimado para foi razoável.
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um duto com parede delgada e sem isolamento térmico, com diâmetro de , é usado para conduzir ar refrigerado a uma vazão de através do sótão de um grande prédio comercial.
O ar no sótão encontra-se a e a circulação natural fornece um coeficiente de transferência de calor por convecção de na superfície externa do duto.
Se o ar refrigerado entra no duto, com de comprimento, a uma temperatura de , quais são a sua temperatura na saída do duto e a taxa de transferência de calor absorvida pelo ar?
As propriedades do ar refrigerado podem ser avaliadas a uma temperatura média estimada de .
Passo 1
Antes de qualquer coisa, vamos definir as propriedades do ar a através da tabela A.4 do Incropera:
Passo 2
A temperatura de saída do ar é dada pela seguinte equação:
A diferença agora é que o coeficiente convectivo é calculado a partir das convecções interna e externa, se liga:
O coeficiente externo já foi dado pelo problema.
Pra calcular o coeficiente convectivo interno, vamos precisar do número de Nusselt, dado por:
Então vamos agora atrás dele.
Passo 3
Para o número de Nusselt, precisaremos do número de Reynolds, dado por:
Como o escoamento interno é turbulento, nem precisamos nos preocupar com as condições do mesmo. Assim, com esse valor de Reynolds e com o valor do número de Prandtl , podemos usar a seguinte correlação:
Como , . Assim substituindo os valores:
O coeficiente convectivo será, então:
Passo 4
O coeficiente convectivo total será dado por:
A temperatura de saída será:
Substituindo os valores:
Passo 5
A taxa de transferência de calor será dada por:
Substituindo os valores:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Óleo a escoa lentamente através de um tubo longo com parede delgada e diâmetro interno de . O tubo está suspenso em uma sala na qual a temperatura do ar é de e o coeficiente de transferência de calor por convecção na superfície externa do tubo é de .
Estime a perda de calor por unidade de comprimento do tubo.
Passo 1
As propriedades do óleo podem ser obtidas na tabela A.5 do Incropera. A , temos que:
Passo 2
A perda de calor por unidade de comprimento pode ser calculada da seguinte forma:
Onde a resistência térmica por unidade de comprimento é dada por:
Dessa equação, temos que encontrar somente o coeficiente convectivo interno.
Passo 3
O coeficiente convectivo interno é dado por:
O problema nos diz que o óleo está escorrendo lentamente, assim, podemos considerar que o escoamento é laminar. Além disso, como o tubo é muito longo, podemos considerar que o mesmo está plenamente desenvolvido.
Dessa forma, considerando condições de temperatura superficial constante, teremos:
Dessa forma, o coeficiente convectivo será:
Passo 4
A resistência térmica por unidade de comprimento será:
Substituindo os valores:
Assim, finalmente, a perda de calor por unidade de comprimento será:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Os gases de exaustão de um forno de processamento de fios são descarregados em uma grande chaminé e as temperaturas do gás da superfície na saída da chaminé devem ser estimadas.
O conhecimento da temperatura de saída do gás é útil para estimar a dispersão dos efluentes na pluma térmica, enquanto o conhecimento da temperatura da superfície de saída da chaminé indica se irá ocorrer a condensação dos produtos gasosos.
A chaminé cilíndrica e com parede delgada possui de diâmetro e de altura. A vazão dos gases de exaustão é de e a temperatura de entrada dos gases é de .
Considere condições nas quais a temperatura do ar ambiente, a velocidade do vento e o coeficiente convectivo externo são de e , respectivamente. Aproximando as propriedades termofísicas do gás por aquelas do ar atmosférico, estime as temperaturas de saída do gás e da superfície da chaminé em sua saída para as condições dadas.
Passo 1
Pra obtermos as propriedades do ar na saída da chaminé, vamos assumir uma temperatura média de saída de , nesse caso:
A essa temperatura, de acordo com a tabela A.4 do Incropera:
Passo 2
A temperatura média de saída dos gases será dada pela seguinte equação:
Onde corresponde ao coeficiente global de transferência de calor, podendo ser calculado da seguinte forma:
Já para a temperatura na superfície na saída dos gases, podemos pensar o seguinte: o fluxo de calor deve ser igual para a convecção interna e para a convecção externa, logo:
Ou seja, encontramos a temperatura média de saída, e depois encontramos a temperatura na superfície de saída.
De qualquer jeito, vamos precisar primeiro do coeficiente convectivo interno , então vamos atrás dele.
Passo 3
O coeficiente convectivo interno é dado por:
Para calcular o número de Nusselt vamos precisar calcular o número de Reynolds, dado por:
Como o escoamento é turbulento, e considerando , teremos:
Dessa forma, o coeficiente convectivo interno será:
Passo 4
Dessa forma, a temperatura média de saída será:
Onde:
Substituindo os valores:
Passo 5
Assim, a temperatura na superfície de saída será dada por:
Reorganizando os termos:
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um tubo de parede delgada, com diâmetro de e comprimento de , é usado para transportar gases de exaustão de uma chaminé até o laboratório, em um prédio próximo, para análise.
O gás entra no tubo a e a uma vazão mássica de . Ventos do outono trocam calor com a parede do tubo com um coeficiente de transferência de calor por convecção de . Considere as propriedades termofísicas dos gases de exaustão iguais à do ar.
Estime o coeficiente de transferência de calor médio para os gases de exaustão escoando no interior do tubo.
Estime o coeficiente global de transferência de calor e a temperatura dos gases de exaustão quando eles chegam ao laboratório.
Passo 1
Estime o coeficiente de transferência de calor médio para os gases de exaustão escoando no interior do tubo.
Antes de qualquer coisa, como precisamos das propriedades do ar, vamos chutar uma temperatura de saída de . Nesse caso:
A essa temperatura, de acordo com a tabela A.4 do Incropera:
Passo 2
O coeficiente convectivo interno é dado por:
Para calcular o número de Nusselt vamos precisar calcular o número de Reynolds, dado por:
Como o escoamento é turbulento, e considerando , teremos:
Dessa forma, o coeficiente convectivo interno será:
Passo 3
Estime o coeficiente global de transferência de calor e a temperatura dos gases de exaustão quando eles chegam ao laboratório.
O coeficiente global de transferência de calor é dado por:
Passo 4
A temperatura média de saída pode ser calculada a partir da seguinte expressão:
Substituindo os valores:
Resposta
;
Exercício Resolvido #8
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Você está projetando um trocador de calor para salas de cirurgia para resfriar sangue (desviado do paciente) de para , pela sua passagem por uma serpentina imersa em um vaso que contém uma mistura de água e gelo.
A vazão volumétrica é de ; o diâmetro do tubo é de ; e e representam as temperaturas de entrada e saída do sangue. Despreze os efeitos da intensificação da transferência de calor associados à curvatura do tubo.
A que temperatura você estimaria as propriedades do fluido ao determinar o valor de em todo o comprimento do tubo?
Se as propriedades do sangue estimadas na temperatura da parta são , , e , qual é o número de Prandtl do sangue?
O escoamento do sangue é laminar ou turbulento?
Desprezando todos os efeitos de entrada e supondo condições plenamente desenvolvidas, calcule o valor de para a transferência de calor no sangue.
Qual é a taxa de perda de calor total no sangue ao passar pelo tubo?
Passo 1
A que temperatura você estimaria as propriedades do fluido ao determinar o valor de em todo o comprimento do tubo?
As propriedades do sangue devem ser estimadas à média das temperaturas de entrada e saída do tubo, logo:
Passo 2
Se as propriedades do sangue estimadas na temperatura da parta são , , e , qual é o número de Prandtl do sangue?
O número de Prandtl é definido por:
Onde , logo:
Passo 3
O escoamento do sangue é laminar ou turbulento?
Para determinar se o escoamento é laminar ou turbulento, vamos precisar calcular o número de Reynolds, dado por:
Onde e , logo:
Onde . Assim, substituindo os valores:
O escoamento é laminar.
Passo 4
Desprezando todos os efeitos de entrada e supondo condições plenamente desenvolvidas, calcule o valor de para a transferência de calor no sangue.
Para o caso de escoamento laminar, plenamente desenvolvido e com condições de temperatura constante na superfície, temos que:
Assim, o coeficiente convectivo será dado por:
Passo 5
Qual é a taxa de perda de calor total no sangue ao passar pelo tubo?
Como temos as temperaturas de entrada e saída do fluido, podemos determinar a taxa de transferência de calor da seguinte forma:
Resposta
O escoamento é laminar.
Exercício Resolvido #9
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um tubo metálico com parede fina e de diâmetro e espessura desprezível, transporta vapor d'água superaquecido à pressão atmosférica e encontra-se pendurado no teto de uma grande sala.
A temperatura do vapor na entrada do tubo é de e a temperatura do ar é de . O coeficiente de transferência de calor por convecção na superfície externa do tubo revestido é de .
Se a velocidade do vapor for de , em que posição ao longo do tubo o vapor irá condensar?
Passo 1
Como estamos trabalhando à pressão atmosférica, o vapor d'água irá condensar quando a temperatura chegar a . Então vamos considerar essa como sendo a “temperatura de saída” pra determinar as propriedades do fluido. Assim:
A essa temperatura, de acordo com a tabela A.6 do Incropera para o vapor d'água:
Passo 2
O comprimento necessário para que a temperatura do vapor chegue a pode ser calculada a partir da seguinte equação:
Reorganizando os termos para isolar o comprimento , teremos:
Onde corresponde ao perímetro do tubo, e o coeficiente convectivo médio é dado por:
Dessa expressão nós temos praticamente tudo, exceto o coeficiente convectivo interno. Então vamos atrás dele.
Passo 3
Para calcular o coeficiente convectivo, precisamos começar calculando o número de Reynolds.
O primeiro é dado por:
Onde o fluxo mássico será dado por:
Assim, o número de Reynolds será:
Ou seja, estamos no regime turbulento. Dessa forma, nem precisamos nos preocupar com a condição do escoamento.
Para este valor de Reynolds e o valor do número de Prandtl , podemos usara seguinte correlação:
Como o fluido está sendo resfriado, . Assim substituindo os valores:
O coeficiente convectivo interno será, então:
Passo 4
O coeficiente convectivo médio será, então:
Passo 5
Finalmente, o comprimento necessário para resfriar o vapor d'água a será:
Resposta
Exercício Resolvido #10
Questão 4, PUCRIO, P2-2003
Água escoa através de um tubo liso, de diâmetro igual a . A água entra na tubulação a e , e é aquecida até uma temperatura igual a . A temperatura da tubulação é mantida a .
Determine o comprimento necessário para o aquecimento. Considere as propriedades da água à temperatura de mistura iguais a: , , , e , e a viscosidade a igual a .
Passo 1
Este se trata de um caso de escoamento interno onde a temperatura superficial é constante. Sendo assim, usaremos essa seguinte expressão:
Reorganizando os termos para isolar o comprimento , teremos:
Dessa expressão nós temos praticamente tudo, exceto o coeficiente convectivo. Então vamos atrás dele.
Passo 2
Para calcular o coeficiente convectivo, precisamos começar calculando o número de Reynolds.
O número de Reynolds é dado por:
Ou seja, estamos no regime turbulento. Dessa forma, nem precisamos nos preocupar com a condição do escoamento.
Para este valor de Reynolds e o valor do número de Prandtl , podemos usar a seguinte correlação:
Assim substituindo os valores:
O coeficiente convectivo será, então:
Passo 3
Assim, o comprimento necessário será:
Onde:
Substituindo os valores:
Resposta
Exercício Resolvido #11
Questão 2, PUC, Lista 2
Óleo motor usado, inicialmente a , escoa através de um tubo de diâmetro interno com vazão de . Este duto é envolto por uma camisa contendo vapor d'água saturado a . Sabendo que o duto tem de comprimento determine a temperatura de saída do óleo.
Passo 1
Como queremos encontrar justamente a temperatura de saída do óleo, vamos chutar uma temperatura de saída de .
Assim, a temperatura média que vamos usar como referência para pegar as propriedades do óleo será:
De acordo com a tabela A.5 do Incropera, para óleo de motor a , teremos:
Passo 2
A temperatura de saída pode ser calculada através da seguinte expressão:
Dessa equação, falta calcular o coeficiente convectivo. Pra calculá-lo, vamos precisar do número de Nusselt, dado por:
Então vamos agora atrás dele.
Passo 3
Para o número de Nusselt, precisaremos do número de Reynolds, dado por:
Opa! Estamos no regime laminar, então precisamos verificar se o escoamento na saída do duto está plenamente desenvolvido, ou na região de entrada térmica.
O comprimento de entrada térmico é dado por:
Ou seja, estamos na região de entrada térmica.
Passo 4
Sabendo que , a correlação mais adequada é a seguinte:
Substituindo os valores:
Dessa forma, o coeficiente convectivo médio será dado por:
Passo 5
A temperatura de saída será:
Onde e:
Substituindo os valores:
Obs.: Caso você considere que a temperatura de saída ficou distante da temperatura que chutamos no início, a boa é refazer o processo, mas usando como “chute” para a temperatura de saída o valor que acabamos de encontrar.
Resposta
Exercício Resolvido #12
Questão 3, UFF, P2-2015.2
(Adaptado) Óleo de motor escoa através de um duto quadrado de de lado e de comprimento a uma vazão de . O óleo entra no duto a uma temperatura de , enquanto que o fluxo de calor pela superfície do duto é mantido constante.
Determine qual a carga térmica que deve ser adicionada ao óleo para que a temperatura do óleo seja de na saída.
As propriedades termofísicas do óleo de motor são dadas pela tabela.
Passo 1
Para determinar as propriedades do óleo de motor, vamos considerar a temperatura média do óleo, dada por:
A essa temperatura, de acordo com a tabela A.5 do Incropera:
Passo 2
Como o fluxo de calor pela superfície do tubo é constante, a temperatura de saída pode ser estimada a partir da seguinte expressão:
Assim, reorganizando os termos pra isolar o fluxo de calor, temos:
Substituindo os valores:
Resposta
Exercício Resolvido #13
Questão 1, UFF, P2-2015.1
Óleo de motor escoa através de um tubo de de diâmetro interno a uma vazão de . O óleo entra no tubo a uma temperatura de , enquanto que a temperatura da superfície do tubo é mantida a . Determine o comprimento do tubo para que a temperatura do óleo seja de na saída. As propriedades termofísicas do óleo de motor são dadas na tabela.
Passo 1
Antes de qualquer coisa, precisamos das propriedades térmicas do óleo. Pra isso, vamos considerar a temperatura média de escoamento, dada por:
De acordo com a tabela A.5 do Incropera, para o óleo de motor a esta temperatura, temos:
Passo 2
Como já temos todas as temperaturas no sistema e este se trata de um caso onde a temperatura superficial é constante, partindo dessa expressão:
Arrumando os termos para isolar o comprimento , teremos:
Dessa expressão nós temos praticamente tudo, exceto o coeficiente convectivo. Então vamos atrás dele.
Passo 3
Para calcular o coeficiente convectivo, precisamos começar calculando o número de Reynolds, dado por
Ou seja, estamos no regime laminar. Vamos assumir que o escoamento esteja plenamente desenvolvido.
Nesse caso, para escoamento plenamente desenvolvido e temperatura superficial constante, o número de Nusselt será:
Por sua vez, o coeficiente convectivo será, então:
Passo 4
Agora podemos finalmente calcular o comprimento adequado para o duto:
Substituindo os valores:
Por via das dúvidas, vamos conferir se fizemos uma boa escolha supondo que o escoamento está plenamente desenvolvido.
O comprimento de entrada térmico é dado por:
Logo, o escoamento estará mesmo plenamente desenvolvido na saída da tubulação.
Resposta
Exercício Resolvido #14
Questão 1, UFRJ, P2-2015.2
Água a e velocidade média de entra em um tubo de de diâmetro, cuja temperatura de parede é mantida em . O comprimento do tubo é de . Calcule:
Coeficiente médio de transferência de calor no tubo;
Temperatura da água na saída do tubo;
Taxa de calor trocado entre o tubo e a água.
Passo 1
Antes de qualquer coisa, precisamos das propriedades da água. Para isso, vamos estimar uma temperatura de saída de . Assim:
Assim, de acordo com a tabela A.6 do Incropera:
Passo 2
Coeficiente médio de transferência de calor no tubo;
O número de Reynolds é dado por:
O regime é laminar.
O comprimento de entrada é dado por:
Assim, o escoamento está na região de entrada térmica. Dessa forma, considerando a temperatura do tubo constante, o número de Nusselt médio será:
Onde, para , . Logo:
Finalmente, o coeficiente convectivo será:
Passo 3
Temperatura da água na saída do tubo;
A temperatura de saída será:
Onde e:
Substituindo os valores:
Passo 4
Taxa de calor trocado entre o tubo e a água.
A taxa de transferência de calor é dada por:
Resposta