Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Escoamento em Dutos Não-Circulares

Ver Todos os Exercícios

Teoria

Introdução

Aqui estamos interessados em trabalhar com o escoamento em dutos cuja seção transversal pode variar de diversas formas.

Por exemplo, vamos resolver a seguinte situação:

Temos um duto de perfil triangular, com 20   m m de lado e 2   m de comprimento, por onde escoa ar com vazão mássica e temperatura média de entrada iguais a, respectivamente 4 × 10 - 4   k g / s e 27 ° C . A superfície do duto é mantida a 100 ° C .

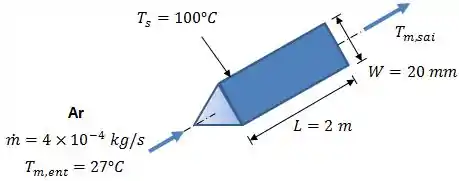
O que queremos responder aqui é: admitindo escoamento plenamente desenvolvido ao longo de todo o duto, qual é a temperatura média de saída do ar?

Assim como fizemos no caso do duto circular, vamos ter que “chutar” uma temperatura de saída para determinarmos as propriedades do ar à temperatura de referência, dada por:

Nesse caso, como a temperatura de entrada T m , e n t = 27 ° C e a superfície é mantida a uma temperatura T s = 100 ° C , vamos chutar aqui uma temperatura de saída T m , s a i = 77 ° C . Fazendo isso, teremos uma temperatura média igual a:

T m = 27 + 77 2 = 52 ° C = 325   K

A essa temperatura, de acordo com a tabela A.4 do Incropera para as propriedades do ar, temos que:

c p = 1008   J / ( k g . K )

μ = 196,4 × 10 - 7   N . s / m 2

k = 0,0282   W / ( m . K )

P r = 0,707

Show de bola! Como temos temperatura superficial constante, a temperatura de saída será dada por:

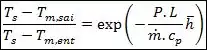
Dessa equação, temos praticamente tudo, exceto o coeficiente convectivo h - , então vamos atrás desse cara.

As correlações para o número de Nusselt são divididas para escoamento laminar e escoamento turbulento. Então, antes, precisamos calcular o número de Reynolds.

Lá e de volta outra vez

Hora de bater aquele papo maroto sobre o número de Reynolds, dado por:

“Beleza! Mas se o duto é não-circular, que valor vamos utilizar para o diâmetro?!”

Nesse caso, nós vamos utilizar o diâmetro hidráulico D h , definido por:

Onde A t r corresponde à área da seção transversal, e P corresponde ao perímetro da seção transversal.

No nosso caso, vamos ter o seguinte:

A t r = B a s e × A l t u r a 2 = 3 W 2 4 = 3 × 20 × 10 - 3 2 4

A t r = 1,73 × 10 - 4   m 2

P = 3 W = 3 × 20 × 10 - 3 → P = 0,06   m

D h = 4 × 1,73 × 10 - 4 0,06 → D h = 0,0115

Assim, o número de Reynolds será:

R e D = m ˙ . D h A t r . μ = 4 × 10 - 4 × 0,0115 1,73 × 10 - 4 × 196,4 × 10 - 7

R e D = 1354

Show de bola, como número de Reynolds é menor que 2300, significa que o escoamento está no regime laminar.

Então estamos prontos pra olhar para as correlações para o número de Nusselt.

Correlações para Escoamento em Dutos Não-Circulares

Para o caso de escoamento laminar, o número de Nusselt N u D é obtido a partir da tabela abaixo:

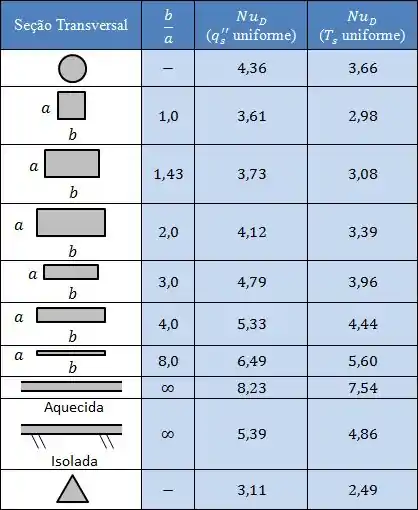
Agora, se o escoamento for turbulento, nós podemos utilizar as mesmas correlações que utilizamos para dutos circulares, se liga:

No nosso caso, como temos um escoamento laminar em um duto com seção transversal triangular, e com temperatura superficial constante, o número de Nusselt será:

N u - D = 2,49

Voltando ao nosso problema

Como já temos o número de Nusselt, o coeficiente convectivo será dado por:

h - = N u - D . k D h = 2,49 × 0,0282 0,0115 → h - = 6,1   W / ( m 2 . K )

Finalmente, a temperatura de saída será dada por:

T s - T m , s a i T s - T m , e n t = exp ⁡ - P . L m ˙ . c p h -

T m , s a i = T s - T s - T m , e n t . exp ⁡ - P . L m ˙ . c p h -

Substituindo os valores, teremos:

T m , s a i = 100 - 100 - 27 . exp ⁡ - 3 × 20 × 10 - 3 × 2 4 × 10 - 4 × 1008 × 6,1

Jogando isso tudo na calculadora, vamos encontrar que:

Nesse caso, a diferença entre a temperatura que encontramos e a que utilizamos no nosso “chute” lá no inicio é pequena, então não precisamos refazer o problema. :)

Vamos fixar isso melhor nos exercícios?! Responde Aí! ;)

Lá e de volta outra vez

Correlações para Escoamento em Dutos Não-Circulares

Voltando ao nosso problema

Exercícios Resolvidos

Exercício Resolvido #1

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

Ar, a 3 × 10 - 4   k g / s e 27 ° C , entra em um duto retangular que possui 1   m de comprimento e 4   m m por 16   m m de lado. Um fluxo térmico uniforme de 600   W / m 2 é imposto na superfície do duto.

Qual é a temperatura do ar e da superfície do duto na sua saída?

Passo 1

Logo de cara, vamos chutar um valor para a temperatura de saída pra definirmos as propriedades do ar.

Como a temperatura de entrada é de 27 ° C   300   K , vamos chutar aqui uma temperatura de saída de 400   K para determinar as propriedades do ar.

Nesse caso:

T m = T m , e n t + T m , s a i 2 = 300 + 400 2 → T m = 350   K

De acordo com a tabela A.4, para as propriedades do ar a 350   K , temos:

c p = 1009   J / ( k g . K )

μ = 208,2 × 10 - 7   N . s / m 2

k = 0,03   W / ( m . K )

P r = 0,7

Passo 2

Como há um fluxo térmico constante na superfície do duto, a temperatura do ar na saída será dada por:

T m , s a i = T m , e n t + q ' ' . A s m ˙ . c p

Onde A s corresponde a toda área superficial do tubo, dada por:

A s = 2 × L × H + 2 × L × W

A s = 2 × 1 × 16 × 10 - 3 + 2 × 1 × 4 × 10 - 3 → A s = 0,04   m 2

Logo:

T m , s a i = 300 + 600 × 0,04 3 × 10 - 4 × 1009

Passo 3

A superfície do duto na região de saída e o ar trocam calor por convecção, de forma que o fluxo térmico é justamente o dado pelo enunciado.

Logo, a temperatura superficial na saída do duto T s , s a i será dada por:

q ' ' = h . T s , s a i - T m , s a i

T s , s a i = T m , s a i + q ' ' h

Show de bola! Então agora precisamos calcular o coeficiente convectivo.

Passo 4

Pra calcular o coeficiente convectivo, precisamos do número de Nusselt, já que:

h = N u D . k D h

Onde o diâmetro hidráulico será dado por:

D h = 4 . A t r P = 4 × 16 × 10 - 3 × 4 × 10 - 3 2 × 16 × 10 - 3 + 4 × 10 - 3 → D h = 6,4 × 10 - 3   m

O número de Reynolds é dado por:

R e D = m ˙ . D h A t r . μ = 3 × 10 - 4 × 6,4 × 10 - 3 16 × 10 - 3 × 4 × 10 - 3 × 208,2 × 10 - 7

R e D = 1441 < 2300

Como estamos no regime laminar, o número de Nusselt é dado pelo valor da tabela na Teoria.

Para b / a = 16 / 4 = 4 :

N u D = 5,33

Dessa forma, o coeficiente convectivo será:

h = N u D . k D h = 5,33 × 0,03 6,4 × 10 - 3 → h = 25   W / ( m 2 . K )

Passo 5

Finalmente, a temperatura superficial na saída do duto será:

T s , s a i = T m , s a i + q ' ' h

Substituindo os valores:

T s , s a i = 379 + 600 25

Resposta

T m , s a i = 379,3   K

T s , s a i = 403   K

Exercício Resolvido #2

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

(Adaptado) Ar a 25 ° C escoa com uma vazão de 30 × 10 - 6   k g / s através de canais com 100   m m de comprimento usados para resfriar um molde metálico de alta condutividade térmica. Suponha que o escoamento esteja fluidodinâmica e termicamente plenamente desenvolvido.

Considere o ar escoando em um canal segmentado em seis seções triangulares de lado a = 5,1   m m . Determine o calor transferido para o ar, quando a temperatura do molde é de 50 ° C .

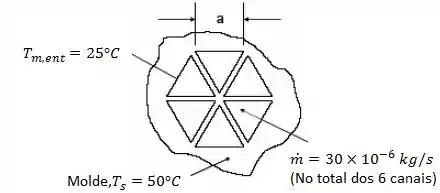
Passo 1

Como não temos a temperatura de saída e este é um problema com temperatura superficial constante, vamos precisar chutar uma temperatura de saída para definir as propriedades do fluido.

Como temos uma temperatura de entrada igual a 25 ° C e o molde está a uma temperatura de 50 ° C , vamos chutar uma temperatura de saída de 49 ° C , bem próximo da temperatura do molde.

Assim, a média das temperaturas de entrada e saída será:

T m = T m , e n t + T m , s a i 2 = 25 + 49 2 = 37 ° C = 310   K

De acordo com a tabela A.4 do Incropera, para o ar a esta temperatura, temos que:

ρ = 1,128   k k g / m 3

c p = 1007   J / ( k g . K )

μ = 189,3 × 10 - 7   N . s / m 2

k = 0,027   W / ( m . K )

Agora estamos prontos pra seguir em frente.

Passo 2

A taxa de transferência de calor será dada por:

q = m . c p . T m , s a i - T m , e n t

Onde a temperatura de saída é dada por:

T s - T m , s a i T s - T m , e n t = exp ⁡ - P . L m ˙ . c p   h -

T m , s a i = T s - T s - T m , e n t . exp ⁡ - P . L m ˙ . c p h -

Pra calcular o coeficiente convectivo, vamos precisar do número de Nusselt:

h - = N u - D . k D h

Então vamos calculá-lo.

Passo 3

Para calcular o número de Nusselt, precisaremos do número de Reynolds, dado por:

R e D = m ˙ . D h A t r . μ

Onde o diâmetro hidráulico é dado por:

D h = 4 . A t r P

A t r = B a s e × A l t u r a 2 = 3 a 2 4 = 1,13 × 10 - 5 m 2

P = 3 a

D h = 4 × 3 a 2 / 4 3 a = 3 a 3 = 3 × 5,1 × 10 - 3 3 → D h = 2,9 × 10 - 3   m

Além disso, como estamos calculando o número de Reynolds em relação para um dos canais, precisamos dividir o fluxo mássico por 6. Dessa forma, o fluxo mássico através de cada canal será:

m ˙ 1 = 30 × 10 - 6 6 = 5 × 10 - 6

Substituindo os valores:

R e D = 5 × 10 - 6 × 2,9 × 10 - 3 1,13 × 10 - 5 × 189,3 × 10 - 7 = 67,78

Opa! Estamos no regime laminar. Assim, pela tabela na teoria, considerando o caso de temperatura superficial constante, o número de Nusselt será:

N u D = 2,49

Assim, o coeficiente convectivo será:

h - = N u - D . k D h = 2,49 × 0,027 2,9 × 10 - 3 → h - = 23,18   W / ( m 2 . K )

Passo 4

A temperatura média de saída do fluido será:

T m , s a i = T s - T s - T m , e n t . exp ⁡ - P . L m ˙ . c p h -

Substituindo os valores:

T m , s a i = 50 - 50 - 25 . exp ⁡ - 3 × 5,1 × 10 - 3 × 0,1 × 23,18 5 × 10 - 6 × 1007

T m , s a i = 49,9 ° C

Passo 5

Finalmente, a taxa de transferência de calor será:

q = m ˙ . c p . T m , s a i - T m , e n t

q = 30 × 10 - 6 × 1007 × 49,9 - 25

Resposta

q = 0,753   W

Exercício Resolvido #3

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

Ar, a 1   a t m e 285   K , entra em um duto retangular com 2   m de comprimento e seção transversal de 75   m m por 150   m m . O duto é mantido a uma temperatura superficial constante de 400   K e a vazão mássica do ar é de 0,10   k g / s .

Determine a taxa de transferência de calor do duto para o ar e a temperatura de saída do ar.

Passo 1

Logo de cara, vamos precisar chutar a temperatura de saída do ar pra determinar as propriedades do ar. Como temos o ar entrando no duto a 285   K e temperatura superficial de 400   K , vamos chutar aqui uma temperatura de saída de 365   K .

De acordo com a tabela A.4 do Incropera, para o ar a essa temperatura, temos:

c p = 1008   J / ( k g . K )

μ = 196,4 × 10 - 7   N . s / m 2

k = 0,0282   W / ( m . K )

P r = 0,707

Vamos seguir em frente.

Passo 2

A taxa de transferência de calor será dada por:

q = m . c p . T m , s a i - T m , e n t

Já a temperatura de saída é dada por:

T s - T m , s a i T s - T m , e n t = exp ⁡ - P . L m ˙ . c p   h -

T m , s a i = T s - T s - T m , e n t . exp ⁡ - P . L m ˙ . c p h -

Vamos precisar então do coeficiente convectivo!

Passo 3

Pra calcular o coeficiente convectivo, vamos precisar do número de Nusselt, se liga:

h - = N u - D . k D h

Para calcular o número de Nusselt, precisaremos do número de Reynolds, dado por:

R e D = 4 . m ˙ π . D h . μ

Onde o diâmetro hidráulico é dado por:

D h = 4 . A t r P = 4 × 150 × 10 - 3 × 75 × 10 - 3 2 × 150 × 10 - 3 + 75 × 10 - 3

D h = 0,10   m

Substituindo os valores:

R e D = 4 × 0,1 π × 0,1 × 196,4 × 10 - 7 → R e D = 64.829

Opa! Estamos no regime turbulento. Assim, pela tabela na teoria, podemos usar a seguinte relação:

N u D - = 0,023 . R e D 4 / 5 . P r 0,4 = 0,023 × 64.829 4 / 5 × 0,707 0,4

N u D - = 141,5

Assim, o coeficiente convectivo será:

h - = N u - D . k D h = 141,5 × 0,02 82 0,1 → h - = 39,9   W / ( m 2 . K )

Passo 4

A temperatura média de saída do fluido será:

T m , s a i = T s - T s - T m , e n t . exp ⁡ - P . L m ˙ . c p h -

Substituindo os valores:

T m , s a i = 400 - 40 0 - 28 5 . exp ⁡ - 2 × 150 × 10 - 3 + 75 × 10 - 3 × 2 × 39,9 0,1 × 100 8

Passo 5

Finalmente, a taxa de transferência de calor será:

q = m ˙ . c p . T m , s a i - T m , e n t

q = 0,1 × 100 8 × 304 - 285

Resposta

T m , s a i = 30 4   K

q = 1915   W

Exercício Resolvido #4

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

(Adaptado) Um fluido refrigerante escoa através de um canal retangular (galeria) no interior do corpo de um molde que é utilizado para produzir peças metálicas.

As dimensões da galeria são a = 90   m m e b = 9,5   m m , e a vazão volumétrica do fluido é de 1,3 × 10 - 3   m 3 / s . A temperatura do refrigerante é de 15 ° C e a parede do molde encontra-se a uma temperatura aproximadamente uniforme de 140 ° C .

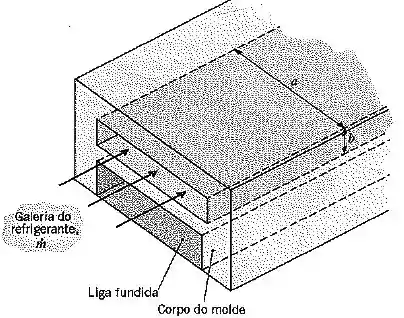
Para minimizar os problemas de corrosão no molde, que é uma peça de custo elevado, é comum se utilizar como fluido refrigerante o etilenoglicol, no lugar de água de processo. Compare os coeficientes convectivos da água e do etilenoglicol nesta aplicação.

Calcule o coeficiente convectivo para a água e para o etilenoglicol.

Passo 1

Para determinar as propriedades dos fluidos, vamos supor que a temperatura de saída do fluido seja igual à temperatura do molde. Dessa forma, a média da temperatura de entrada e saída será:

T m = T m , s a i + T m , e n t 2 = 140 + 15 2 → T m = 77,5 ° C = 350,5   K

De acordo com a tabela A.6 do Incropera, para as propriedades da água, temos que:

ρ = 974   k g / m 3

μ = 365 × 10 - 6   N . s / m 2

k = 0,668   W / ( m . K )

P r = 2,29

E, de acordo com a tabela A.5 do Incropera, para as propriedades do etilenoglicol, temos que:

ρ = 1079   k g / m 3

υ = 3,17 × 10 - 6   N . s / m 2

k = 0 , 261   W / ( m . K )

P r = 34,6

Passo 2

Vamos começar resolvendo o problema para a água.

Pra calcular o coeficiente convectivo, vamos precisar do número de Nusselt, se liga:

h - = N u - D . k D h

Para calcular o número de Nusselt, precisaremos do número de Reynolds, dado por:

R e D = ρ . u m . D h μ = 4 . m ˙ π . D h . μ

Onde o diâmetro hidráulico é dado por:

D h = 4 . A t r P = 4 × 90 × 10 - 3 × 9 , 5 × 10 - 3 2 × 90 × 10 - 3 + 9,5 × 10 - 3

D h = 0 , 0172   m

Além disso, a velocidade média do fluido é dada por:

u m = V ˙ A t r = 1,3 × 10 - 3 90 × 10 - 3 × 9,5 × 10 - 3 → u m = 1,52   m / s

Substituindo os valores:

R e D = 974 × 1,52 × 0,0172 365 × 10 - 6 → R e D = 6 9.765

Opa! Estamos no regime turbulento. Assim, pela tabela na teoria, podemos usar a seguinte relação:

N u D - = 0,023 . R e D 4 / 5 . P r 0,4 = 0,023 × 69.765 4 / 5 × 2,29 0,4

N u D - = 240

Assim, o coeficiente convectivo será:

h - a = N u - D . k D h = 240 × 0 , 668 0 , 0172

Passo 3

Repetindo os cálculos para o etilenoglicol, temos que o número de Reynolds é dado por:

R e D = u m . D h υ = 1,52 × 0,0172 3,17 × 10 - 6 → R e D = 8.247

Opa! Como estamos novamente no regime turbulento, vamos utilizar a mesma correlação para o número de Nusselt.

N u D - = 0,023 . R e D 4 / 5 . P r 0,4 = 0,023 × 8.247 4 / 5 × 34,6 0,4

N u D - = 129

Assim, o coeficiente convectivo será:

h - e = N u - D . k D h = 129 × 0,261 0,0172

Resposta

h - a = 9326   W / ( m 2 . K )

h - e = 1957   W / ( m 2 . K )

Exercício Resolvido #5

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

(Adaptado) Você foi requisitado para efetuar um estudo de viabilidade do projeto de um aquecedor de sangue para ser usado durante processos de transfusão de sangue. Esse trocador deve aquecer o sangue oriundo do banco de sangue de 10 ° C a 37 ° C ,a uma vazão de 200   m l / m i n .

O sangue passa através de um tubo com seção transfusão retangular; 6,4   m m por 1,6   m m ; formado entre duas placas que são mantidas a uma temperatura constante de 40 ° C .

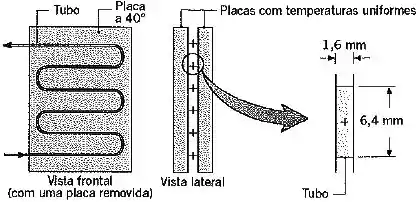
Calcule o comprimento de tubo necessário para atingir as condições de saída desejadas com a vazão especificada. Considere o escoamento plenamente desenvolvido e que o sangue possua as mesmas propriedades da água.

Dado: Considere a taxa de transferência de calor dada por q = h - . A l a t . Δ T m l , onde Δ T m l = 11,7 ° C e A l a t corresponde à área lateral do tubo.

Passo 1

Logo de cara precisamos determinar as propriedades da água, para isso, usaremos a média das temperaturas de entrada e saída, dadas por:

T m = T m , s a i + T m , e n t 2 = 37 + 1 0 2 → T m = 23,5 ° C = 296,5   K

De acordo com a tabela A.6 do Incropera, para as propriedades da água líquida, temos que:

c p = 4179   J / ( k g . K )

ρ = 997   k g / m 3

υ = 8,58 × 10 - 7   m 2 / s

k = 0,613   W / ( m . K )

P r = 5,83

Passo 2

Podemos encontrar o comprimento adequado para o tubo utilizando a expressão para a taxa de transferência de calor, dada por:

m ˙ . c p . T m , s a i - T m , e n t = h - . A . Δ T m l

Onde A l a t = P . L , sendo P o perímetro da seção transversal. Dessa forma:

L = m ˙ . c p . T m , s a i - T m , e n t h - . P . Δ T m l

Dessa equação, precisamos calcular o coeficiente convectivo, então vamos atrás dele.

Passo 3

Para encontrar o coeficiente convectivo, precisamos do número de Reynolds, dado por:

R e D = u m D h υ

Onde o diâmetro hidráulico é dado por:

D h = 4 A t r P = 4 × 6,4 × 10 - 3 × 1,6 × 10 - 3 2 × 6,4 × 10 - 3 + 1,6 × 10 - 3

D h = 2,56 × 10 - 3   m

Além disso, a velocidade é dada por:

u m = m ˙ ρ . A t r = ρ . V ˙ ρ . A t r = V ˙ A t r

Onde:

V ˙ = 200 m l m i n × 1 60 m i n s × 10 - 6 m 3 m l → V ˙ = 3,33 × 10 - 6   m 3 / s

Logo:

u m = 3,33 × 10 - 6 6,4 × 10 - 3 × 1,6 × 10 - 3 → u m = 0,326   m / s

Finalmente, o número de Reynolds será:

R e D = u m D h υ = 0,326 × 0,00256 8,58 × 10 - 7 = 873

Como o escoamento é laminar, considerando o mesmo totalmente desenvolvido, com temperatura superficial constante e razão b / a = 6,4 / 1,6 = 4 , temos que o número de Nusselt será:

N u D = 4,44

Assim, o coeficiente convectivo será:

h = N u D . k D h = 4,44 × 0,613 0,00256 → h = 1063   W / ( m 2 . K )

Passo 4

Voltando à expressão de L , temos:

L = m ˙ . c p . T m , s a i - T m , e n t h - . P . Δ T m l

Onde:

m ˙ = ρ . A t r . u m = 997 × 6,4 × 10 - 3 × 1,6 × 10 - 3 × 0,326

m ˙ = 3,328 × 10 - 3   k g / s

Finalmente:

L = 3,328 × 10 - 3 × 4179 × 37 - 10 1063 × 2 × 6,4 × 10 - 3 + 1,6 × 10 - 3 × 11,7

Resposta

L = 1,9   m

Exercício Resolvido #6

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

(Adaptado) Um equipamento que recupera calor de produtos de combustão a altas temperaturas envolve a passagem do gás de combustão entre placas paralelas, que são mantidas, cada uma, a 350   K pelo escoamento de água sobre as respectivas superfícies externas.

A separação entre as placas é de 40   m m e o escoamento do gás é plenamente desenvolvido. Pode ser considerado que as propriedades do gás são iguais às do ar atmosférico e as duas temperatura e velocidade médias são 1000   K e 60   m / s , respectivamente.

Qual é o fluxo térmico na superfície das placas?

Passo 1

De acordo com a tabela A.4 do Incropera para o ar, as propriedades do gás são:

ρ = 0,348   k g / m 3

μ = 424,4 × 10 - 7   k g / ( s . m )

k = 0 , 0667   W / ( m . K )

P r = 0,726

Passo 2

O fluxo térmico é dado por:

q ' ' = h . T m - T s

Dessa equação, precisamos ir atrás do coeficiente convectivo.

Passo 3

O coeficiente convectivo é dado por:

h = N u D . k D h

Para calcular o número de Nusselt, precisamos do número de Reynolds, dado por:

R e D = ρ . u m . D h μ

Onde, no caso de placas paralelas, o diâmetro hidráulico é dado por:

D h = 2 H = 2 × 40 × 10 - 3 = 0,08   m

Onde H é a separação entre as placas.

Dessa forma:

R e D = 0,348 × 60 × 0,08 424,4 × 10 - 7 → R e D = 39360

Nesse caso, o número de Nusselt é dado por:

N u D = 0,023 . R e D 4 / 5 . P r 0 , 3 = 0,023 × 39 . 360 4 / 5 × 0,726 0 , 3

N u D - = 99,1

Assim, o coeficiente convectivo será:

h = N u D . k D h = 99,1 × 0 , 0667 0,0 8 → h = 82,6   W / ( m 2 . K )

Passo 4

Finalmente, o fluxo térmico será:

q ' ' = h . T m - T s = 82,6 × 1000 - 350

Resposta

q ' ' = 53.700   W / m 2

Exercícios de Livros Relacionados

Ar 1a t m entra em tubo circular de 5c m de diâmetro a 20 ℃ ℃ com velocidade média de 5m / s . A parede do tubo é mantida a uma temperatura de superfície constante de 160 ℃ ℃ e a temperatura média na
Ar a 20 ℃ ℃ 1a t m , entra em tubo circular de 5m m de diâmetro e 10c m de comprimento com velocidade média de 5m / s . A parede do tubo é mantida a uma temperatura de superfície constante de 160 ℃ ℃.
Água escoa com vazão mássica de 0,7k g / s por um tubo anelar concêntrico a uma temperatura média de entrada e de saída de 20 e 80 ℃ ℃, respectivemente. O tubo anelar concêntrico tem diâmetro interno
Repita o Prob. 8-64 para um duto horizontal circular de 15c m de diâmetro.
Um computador resfriado por ventilação contém oito placas de circuito impresso (PCI), cada uma dissipando 12W de potência. As placas têm 12c m de altura e 15c m de comprimento. A folga entre as pontas