Espessura de Camada-Limite
Produzido por Raphael EloiTeoria
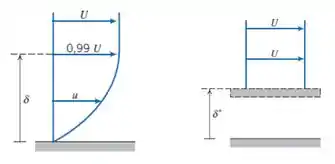
De que maneira você delimitaria o “tamanho” da camada-limite? Em que altura a velocidade pode ser considerada constante ()?
Pra gente definir em que ponto isso ocorre, surgem as definições de espessura de camada-limite. Elas têm o objetivo de quantificar o “tamanho” dessa região e podem ser classificadas basicamente em três tipos: espessura de perturbação (), de deslocamento () e de quantidade de movimento (). Bora dar uma olhada em cada uma delas!
Espessura de Perturbação ()
Essa é a definição mais simples e, por isso, a mais usada. Ela define que a camada-limite termina na distância da superfície, onde a velocidade do fluido equivale a da velocidade de corrente livre ():
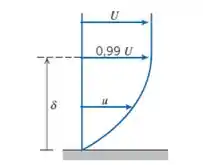
Você poderia pensar: “Por que eu não defino a espessura como sendo a distância na qual a velocidade é exatamente igual a ?”.
Seria bem bacana, não é mesmo? Mas lembre-se de que a velocidade se aproxima assintoticamente de , ou seja, ela chega perto de , mas nunca é exatamente esse valor. Então, nós precisamos estabelecer um critério que seja real, por isso o “99%”. :)
Espessura de Deslocamento ()
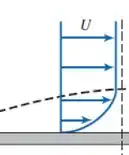
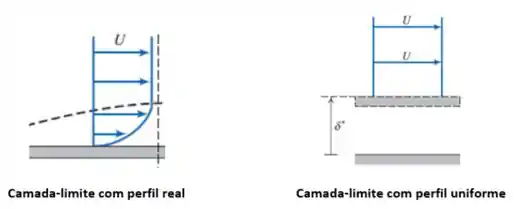
Ela representa a distância da qual a superfície deveria ser deslocada para uma corrente com perfil de velocidades uniforme (invíscida) produzir o mesmo escoamento volumétrico que o escoamento real do fluido.

Calma, pequeno gafanhoto! Ahah Bora entender isso juntos! A gente sabe que o perfil de velocidade tem aquela cara bem famosa, com o gradiente :
Imagina que a gente tá interessado em calcular a vazão num duto de seção quadrada (4 placas planas unidas). Sabemos que a vazão volumétrica pode ser escrita como o produto da velocidade pela área transversal ao escoamento:
Para um elemento infinitesimal, temos que:
Integrando a expressão de até :
Mas é bem chato trabalhar com essa função nas nossas contas. Não seria bem mais fácil se a velocidade fosse sempre constante e saísse da integral? Pois é! Não é que arrumaram um jeitinho de fazer isso!?
A gente tem uma quantidade definida de fluido que passa através de uma região (vazão volumétrica). A ideia da espessura de deslocamento é propor um perfil de velocidades constante, mas que tenha a mesma vazão volumétrica que o perfil observado no escoamento real (com o gradiente de velocidades).
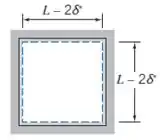
Imagine, por exemplo, que o duto quadrado tem de lado e que um fluido vai entrar nele com uma velocidade de . Se eu te disser que em determinado ponto, a espessura de deslocamento equivale a , no que isso facilita sua vida?
Isso significa que resolver esse problema com aquele perfil chato num duto de lado dá no mesmo que resolver um problema em que o duto de lado “” com o perfil uniforme (). Ou seja, a gente desloca o início do perfil em em cada uma das placas. D
Dá uma olhada na imagem aqui pra ver como fica:
Então no nosso caso, se quiséssemos calcular a vazão nesse ponto por exemplo, ao invés de usar o duto com lado e o perfil de velocidades real (), vamos usar um duto de lado com o perfil uniforme hipotético ():
Bem mais fácil, não? :) Então, já sabe! Se já tiver informação da espessura de deslocamento () fica fácil!
Para que a gente garanta que o escoamento volumétrico com o perfil uniforme () seja o mesmo que com o perfil real (), podemos igualar a vazão de um com a de outro:
Após alguns “algebrismos”, chegamos à definição matemática da espessura de deslocamento:
Espessura de Quantidade de Movimento ()
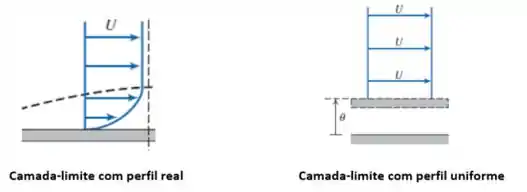
Representa a distância da qual a superfície deveria ser deslocada para uma corrente com perfil de velocidades uniforme (invíscida) produzir o mesmo momento linear que o escoamento real do fluido.

Agora não assusta mais! É parecido com a anterior. A ideia da espessura de quantidade de movimento é propor um perfil de velocidades uniforme (velocidades constantes), mas que tenha o mesmo momento linear (quantidade de movimento).
Sabemos que o momento linear pode ser escrito como sendo o produto da densidade pelo quadrado da velocidade:
Para um elemento infinitesimal, temos que:
Integrando a expressão de até :
Lembra que igualamos as expressões de vazão volumétrica no caso da espessura de deslocamento? Pois é, na espessura de quantidade de movimento, vamos igualar as expressões de momento linear:
De maneira semelhante ao que vimos para a espessura de deslocamento, chegamos à definição matemática da espessura de quantidade de movimento:
Na prática, funciona da mesma forma que a de deslocamento, só que com um critério diferente: mesmo momento linear e não vazão volumétrica!
Craques em camada-limite agora? Vamos exercitar? Então, responde aí! ^^
Espessura de Deslocamento ( δ * )
Espessura de Quantidade de Movimento ( θ )
Exercícios Resolvidos
Exercício Resolvido #1
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C. Introdução à Mecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
Uma aproximação para o perfil de velocidade em uma camada-limite laminar é:
Essa expressão satisfaz as condições de contorno aplicáveis ao perfil de velocidade da camada-limite laminar? Avalie e .
Passo 1
Neste exercício, nós já temos o perfil de velocidades descrito e o enunciado pede para só conferirmos as condições de contorno. Mais tranquilo que o exercício anterior, não é mesmo?
Além disso, temos que avaliar as razões das espessuras de deslocamento () e de quantidade de movimento () sobre a espessura de perturbação ().
Então, vamos começar pelo mais simples: avaliar a coerência do perfil de velocidades proposto!
Lembre-se de que, na camada-limite, a velocidade do fluido em contato com a superfície é zero (condição de não-deslizamento):
Certinho! Agora, na região mais afastada, a tensão de cisalhamento é nula ():
É, até que esse cara sabe fazer bem um perfil, tudo certinho! ^^
Passo 2
Agora, vamos aplicar as definições que vimos de espessura de camada-limite!
Antes de começar, vamos propor uma troca de variável, tal que . Mas por que isso? Dê uma olhadinha no perfil de velocidades do enunciado. Não ficaria bem mais limpo e organizado se trocássemos todas as razões por ? Então, é isso que vamos fazer! ^^
Assim, ficamos com:
Bem melhor, não? Isso facilitará nossa vida adiante!
Para a espessura de deslocamento ():
Como é uma constante, podemos passar ela para dentro da derivada e ficamos com:
Olha só, aparece aquela nossa nova variável . Então, vamos reescrever em função dela:
Note que o limite de integração superior também muda, pois, se , então e, se , então .
Substituindo a expressão do perfil de velocidades, temos:
Ao integrarmos:
Logo:
Passo 3
Analogamente, para a espessura de quantidade de movimento ():
Fazendo a mudança de variáveis, temos:
Ao substituirmos a expressão do perfil:
Logo:
Resposta
Sim, o perfil proposto satisfaz as condições de contorno! E as razões entres as diferentes espessuras de camada-limite são dadas abaixo:
Exercício Resolvido #2
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C. Introdução à Mecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
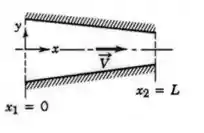
Um fluido de massa, específica , escoa a sobre uma placa plana de de comprimento e de largura. Na borda de fuga, a espessura da camada-limite é . Considere que o perfil de velocidade é linear, conforme mostrado, e que o escoamento é bidimensional (as condições de escoamento são independentes de ). Usando o volume de controle , mostrado por linhas tracejadas:
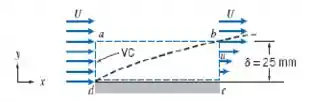
Calcule a vazão através da superfície .
Determine a força de arrasto sobre a superfície superior da placa.
Passo 1
Vamos inicialmente organizar nossos objetivos! O enunciado nos pede 2 coisas: a vazão de fluido através da superfície e a força de arrasto sobre a superfície.
O cálculo da vazão é feito pelo balanço de massa que já vimos anteriormente no tópico de Forma Integral do Volume de Controle:
Note que precisaremos do perfil de velocidades para calcular a vazão, mas qual é sua expressão?
O enunciado nos diz que o perfil é linear, logo é do tipo:
Lembra das condições de contorno? Então, sabemos que a velocidade é nula em e que equivale a em . Portanto:
E ainda:
Pronto! Temos que o perfil de velocidades é dado por:
Podemos reescrevê-lo com a variável :
Passo 2
Considerando o retângulo como volume de controle (VC) e que o problema está no estado estacionário (propriedades não variam no tempo), podemos escrever:
Como são e são constantes, podem sair das derivadas e integrais:
Substituindo a expressão do perfil de velocidades que encontramos:
Pela mudança de variável, temos:
Logo:
Substituindo na integral:
Passo 3
Vamos agora concluir nosso segundo objetivo: determinar a força de arrasto que a superfície da placa sofre devido ao escoamento do fluido.
Se antes utilizamos o balanço de massa para encontrar a vazão, agora, como queremos encontrar uma força, utilizaremos o balanço de momento:
Como assumimos estado estacionário e o volume de controle não se move simultaneamente ao fluido ():
Resposta
Exercício Resolvido #3
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C. Introdução à Mecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
Ar escoa na região de entrada de um duto quadrado, conforme mostrado. A velocidade é uniforme, , e o duto tem área de . Em uma seção a a jusante da entrada, a espessura de deslocamento, , em cada parede mede . Determine a variação de pressão entre as seções e.
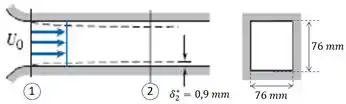
Passo 1
E aí, entendeu o problema? O enunciado nos pede para calcular a diferença de pressão entre os dois pontos. Mas por que há essa diferença? Chegou a pensar nisso?
Sabemos que pressão e velocidade estão correlacionados pela equação de Bernoulli:
Então, para que exista uma diferença de pressão entre e , significa dizer que há também uma diferença entre as velocidades médias dos pontos e . E você saberia explicar o porquê dessa diferença de velocidades?
Para isso, temos que lembrar da definição de espessura de deslocamento (). Ela é a distância da qual a superfície deve ser deslocada, tal que o fluxo volumétrico real possa ser calculado por meio de um perfil uniforme (velocidades constantes).
Como nos foi dado o valor dessa espessura, podemos considerar o escoamento nesse duto como se ele fosse em um duto convergente, ou seja, cuja área diminui ao longo do escoamento:
Como a vazão é constante, sabemos que ao diminuir a área do escoamento, aumentamos a velocidade média do fluido e, consequentemente, diminuímos a pressão. Sendo assim, esperamos que .
Vamos conferir se isso condiz com o resultado?
Passo 2
Pela equação da conservação da massa, admitindo estado estacionário, temos que:
Sendo assim:
Como as velocidades e são constantes:
O cálculo das áreas será dado por:
Já sabemos que no início (ponto ), a camada-limite ainda não se formou e a velocidade média do escoamento equivale à do fluido antes de entrar (. Dessa maneira:
Passo 3
Pela equação de Bernoulli aplicada aos pontos e :
Olha que bacana! De fato, a diferença de pressão deu negativa como havíamos predito ao início!
Então aprendemos que: em dutos com contração, a velocidade média aumenta ao longo do escoamento e que, em regiões com maiores velocidades, observamos menores valores de pressão (para um determinado sistema com energia fixada).
Resposta
Exercício Resolvido #4
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C. Introdução à Mecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
O perfil de velocidade senoidal mais geral para o escoamento laminar da camada-limite sobre uma placa plana é . Estabeleça três condições de contorno aplicáveis ao perfil de velocidade laminar de camada-limite. Avalie as constantes A, B e C.
Passo 1
A ideia com esse exercício é fixar as condições de contorno usualmente utilizadas, para se determinar o perfil de velocidades na camada-limite desenvolvida sob uma placa plana.
Nosso objetivo é aplicar três condições de contorno na equação senoidal, a fim de encontrar os três parâmetros: A, B e C.
A condição de contorno mais importante da Mecânica dos Fluidos é a condição de aderência (ou de não-deslizamento), que afirma que a velocidade no fluido em contato com uma superfície em repouso é nula.
Além disso, podemos ainda definir mais duas condições para camada-limite, que tratam do fato da velocidade ser constante () e da tensão de cisalhamento ser nula fora da camada-limite ().
Com isso temos as seguintes condições:
Passo 2
Definidas as condições de contorno, vamos aplicar cada uma delas à equação:
Pela condição de não-deslizamento:
Pela condição da continuidade do perfil de velocidades com :
Pela condição de tensão cisalhante nula fora da camada-limite:
Sabemos que a função cosseno se anula toda vez que seu argumento for múltiplo de , logo:
Substituindo na equação da segunda condição, obtemos:
Dessa maneira, temos a equação completa:
Resposta
Condições de contorno:
Valores das constantes:
Exercício Resolvido #5
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 583, ex. 9.10
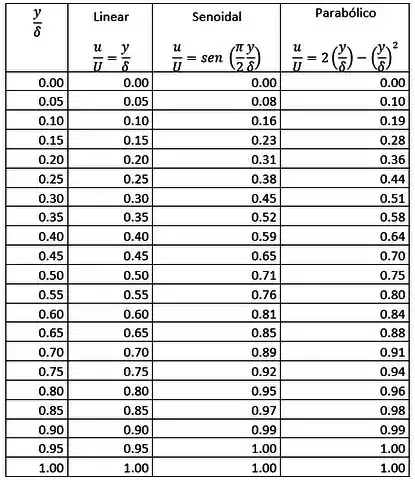
Os perfis de velocidade das camadas-limite laminares frequentemente são aproximados pelas equações
Linear:
Senoidal:
Parabólico:
Compare as formas destes perfis de velocidade, traçando um gráfico de (na ordenada) como uma função de (na abscissa).
Passo 1
Nesse exercício já temos o comportamento de três tipos de camadas-limite laminares. Isso já é um adianto o/
Para traçar o gráfico, vamos pegar alguns valores de y e aplicar as fórmulas dadas no enunciado separadamente. Os valores estão na tabela
Por último, vamos fazer o gráfico com esses valores. Antes, atençãããão! O eixo y será a distância adimensional, ou seja, . E no eixo x estarão as velocidades adimensionais (u/U).
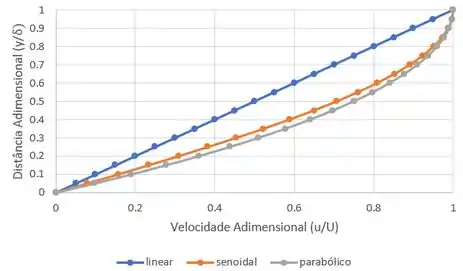
E assim conseguimos aproximar camadas-limites laminares como essa:
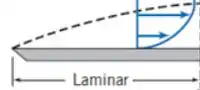
Nesse caso, o comportamento que melhor se encaixa é o parabólico ou o senoidal 😉
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 584, ex. 9.15
Avalie θ/δ para cada um dos perfis de velocidade da camada-limite linear dados a seguir:
Linear:
Senoidal:
Parabólico:
Passo 1
O que queremos dessa vez? Queremos calcular a razão entre a espessura de quantidade de movimento (θ) e a espessura de perturbação (δ) para cada um dos tipos de camada-limite apresentados.
Vimos na teoria, a definição de θ
Dividindo pela espessura de perturbação
A sacada aqui é uma pequena mudança de variáveis que vai facilitar as coisas
Atualizando a integral
Agora vamos substituir os diferentes perfis de velocidade. No perfil linear:
Substituindo
Então, a razão entre as espessuras no perfil linear é
Passo 2
Analisando o perfil senoidal
Substituindo na equação da espessura de quantidade de movimento
Integrando seno ao quadrado por partes
Encontramos a razão para o perfil senoidal. o/
Passo 3
Finalmente, para o perfil parabólico
Substituindo em
Integrando
Então, a relação entre as espessuras no perfil parabólico é
Resposta
Linear:
Senoidal:
Parabólico:
Exercício Resolvido #7
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 584, ex. 9.16
Avalie para cada um dos perfis de velocidade da camada-limite linear dados a seguir:
Linear:
Senoidal:
Parabólico:
Passo 1
Ei! Esse exercício é parecido com o anterior, porém! Agora queremos calcular a razão entre a espessura de deslocamento e a espessura de perturbação δ para cada um dos tipos de camada-limite apresentados.
Vamos lembrar da definição de
Sim, é parecido com a espessura de quantidade de movimento θ, mas não é igual! Olha aí
Fique atento nas fórmulas. Combinado? o/ Voltando a espessura de deslocamento . Dividindo pela espessura de perturbação δ
Vamos fazer uma mudança de variáveis para nos facilitar na integração
Atualizando a integral
Estamos prontos para substituir os diferentes perfis de velocidade. No perfil linear:
Substituindo na equação da espessura de camada-limite de deslocamento
Logo, a razão entre as espessuras no perfil linear é
Show! Vamos para o próximo perfil de velocidades na camada-limite
Passo 2
Vamos analisar o perfil senoidal e escrever em função da nova variável η
Substituindo na equação da espessura de deslocamento
Essa é a relação para o perfil senoidal:
Passo 3
Para terminar, vamos analisar o perfil parabólico e escrever em função da nova variável η
Substituindo na equação da espessura de deslocamento
Integrando
Então, a relação entre as espessuras no perfil parabólico é
Resposta
Linear:
Senoidal:
Parabólico:
Exercício Resolvido #8
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 584, ex. 9.17
Avalie e θ para o perfil de velocidade turbulento da lei de potência 1/7 apresentado abaixo. Compare com as razões para o perfil parabólico de velocidade de camada-limite laminar dado.
Lei de Potência 1/7:
Parabólico:
Passo 1
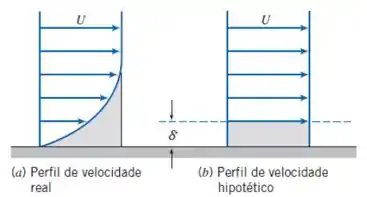
Nesse exercício queremos comparar as espessuras das camadas limites para duas diferentes formas: uma laminar e outra turbulenta.
Para o perfil turbulento, foi dada uma lei de potência que fornece uma camada mais achatada, enquanto no perfil laminar, ela é mais acentuada
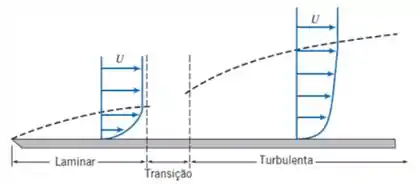
Pela figura já podemos esperar que a relação entre as espessuras da laminar será maior que a da turbulenta.
Vamos verificar isso em números tanto para a espessura de deslocamento em relação a de perturbação δ como para a espessura de quantidade de movimento θ em relação a δ
Para a espessura de deslocamento, temos essa equação
Dividindo pela espessura de perturbação δ já que queremos encontrar essa razão
Fazendo uma mudança de variáveis para facilitar a solução da integral
Atualizando a equação
Agora vamos analisar o perfil de lei de potência 1/7 turbulento e substituir a nova variável
Voltando à equação
Resolvendo
Encontramos a razão entre a espessura de deslocamento e a de perturbação para o perfil turbulento. Vamos comparar com o laminar parabólico
Substituindo na equação da espessura de deslocamento
Integrando
Então, a relação entre as espessuras no perfil parabólico é
Com isso, vemos que a relação é
Ou seja, a espessura da camada-limite de deslocamento em relação a de perturbação é menor para o escoamento turbulento, como esperávamos :D
Passo 2
Agora vamos analisar a espessura de quantidade de movimento, definida assim:
Dividindo pela espessura de perturbação
Utilizando a variável
Finalmente, vamos substituir os perfis de velocidade. Primeiro, o turbulento
A relação entre espessura de quantidade de movimento e de perturbação no perfil turbulento estudado é
Analisando o perfil parabólico laminar
Substituindo em
Integrando
Então, a relação entre as espessuras no perfil parabólico é
Com isso, encontramos todas as relações como esperado, a relação no escoamento laminar é maior que no escoamento turbulento.
Resposta
Parabólico Laminar:
Lei de potências 1/7 Turbulento: