Exercícios de Espessura de Camada-Limite - Lista de Exercícios Resolvida

Uma aproximação para o perfil de velocidade em uma camada-limite laminar é:

Essa expressão satisfaz as condições de contorno aplicáveis ao perfil de velocidade da camada-limite laminar? Avalie e .

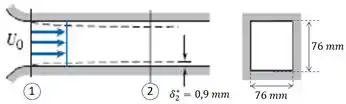
Ar escoa na região de entrada de um duto quadrado, conforme mostrado. A velocidade é uniforme, , e o duto tem área de . Em uma seção a a jusante da entrada, a espessura de deslocamento, , em cada parede mede . Determine a variação de pressão entre as seções e.

Avalie e θ para o perfil de velocidade turbulento da lei de potência 1/7 apresentado abaixo. Compare com as razões para o perfil parabólico de velocidade de camada-limite laminar dado.

Lei de Potência 1/7:

Parabólico:

Os perfis de velocidade das camadas-limite laminares frequentemente são aproximados pelas equações

Linear:

Senoidal:

Parabólico:

Compare as formas destes perfis de velocidade, traçando um gráfico de (na ordenada) como uma função de (na abscissa).

O perfil de velocidade senoidal mais geral para o escoamento laminar da camada-limite sobre uma placa plana é . Estabeleça três condições de contorno aplicáveis ao perfil de velocidade laminar de camada-limite. Avalie as constantes A, B e C.

Um fluido de massa, específica , escoa a sobre uma placa plana de de comprimento e de largura. Na borda de fuga, a espessura da camada-limite é . Considere que o perfil de velocidade é linear, conforme mostrado, e que o escoamento é bidimensional (as condições de escoamento são independentes de ). Usando o volume de controle , mostrado por linhas tracejadas:

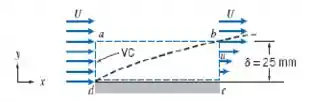
Calcule a vazão através da superfície .

Determine a força de arrasto sobre a superfície superior da placa.

Avalie para cada um dos perfis de velocidade da camada-limite linear dados a seguir:

Linear:

Senoidal:

Parabólico:

Avalie θ/δ para cada um dos perfis de velocidade da camada-limite linear dados a seguir:

Linear:

Senoidal:

Parabólico: