Força de Arrasto
Teoria
Opa! Bora conversar sobre Força de Arrasto?! Vem com o Responde Aí!
O que é Força de Arrasto?
A força de arrasto ou força de arraste (fica a gosto do freguês 🤣) é a força de resistência ao movimento de um objeto em um meio fluido, essa força atua no sentido oposto ao movimento do objeto no meio.
-Hãam? 😖
A força de arrasto
Bora ver essa parada direitinho!
Arrasto de Atrito
Quando o fluido escoa sobre uma superfície, o movimento das moléculas na região perto da parede é desacelerado. A gente pode entender a resistência ao escoamento como se houvesse uma força de atrito entre o fluido e a parede, parecido com o atrito que vemos na Física em Mecânica.
Nesse vídeo a gente explica tudo o que você precisa saber sobre força de arrasto, arrasto de atrito de pressão e muito mais! Dá só uma conferida!
Pra facilitar, imagine um corpo que tenta se mover através de um fluido, como uma bola de futebol voando até o gol depois de um chute. A bola terá seu movimento dificultado porque o fluido interage com a sua superfície.
Mas você também pode pensar na situação contrária, em que o objeto está parado e o fluido escoa sobre ele. Nesse último caso, a força de atrito será a responsável por arrastar o objeto como mostrado abaixo:
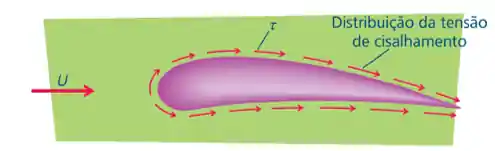
As forças geradas pela tensão de cisalhamento causam o arraste do objeto, como indicado na figura. Esse fenômeno é denominado de arrasto por atrito. Uma observação importante é que, quanto mais “lento” for o fluxo e mais lisa for a superfície, menos expressivo será o arrasto por atrito.
Arrasto de Pressão
Quando um fluido escoa sobre uma esfera, por exemplo, ele exerce uma determinada pressão na parte dianteira, onde ocorre o choque do fluido com a esfera. A pressão exercida sobre ela é máxima no ponto central e diminui ao longo da superfície. Já a parte traseira da esfera não está sofrendo o impacto do fluido, então apresenta uma pressão menor.
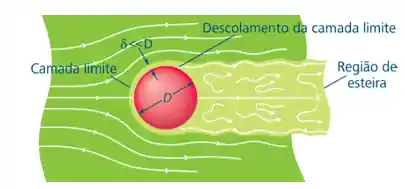
Dessa forma, o objeto tem uma região de alta pressão na parte dianteira (impacto do fluido) e outra de baixa pressão na parte traseira (região de esteira), gerando uma força da esquerda para a direita, na figura, que “arrasta” a esfera. Esse fenômeno é o arrasto de pressão.
Coeficiente de Arrasto
Em resumo, a intensidade do arrasto depende da forma do objeto e das características do escoamento. Para quantificarmos a influência do tipo de geometria na força de arrasto, a gente define um número adimensional chamado de coeficiente de arrasto
Esse coeficiente de arrasto leva em consideração tanto o arrasto de atrito, quanto o de pressão e pode ser definido matematicamente como a razão entre a força real a que um objeto é submetido ao escoar por um fluido
Sendo assim, esperamos que, quanto maior o valor de
-“Como assim?”
No exemplo de uma partícula esférica, a área que utilizamos no cálculo é a área do círculo projetada como ilustrado abaixo e não a área total de uma esfera:
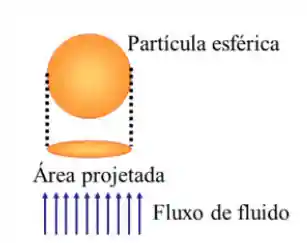
Então, para uma esfera de raio
Mas a gente não trabalha só com esferas, não é mesmo?
Tabela de Coeficiente de Arrasto
Existem várias geometrias e, para cada uma delas, teremos um coeficiente de arrasto
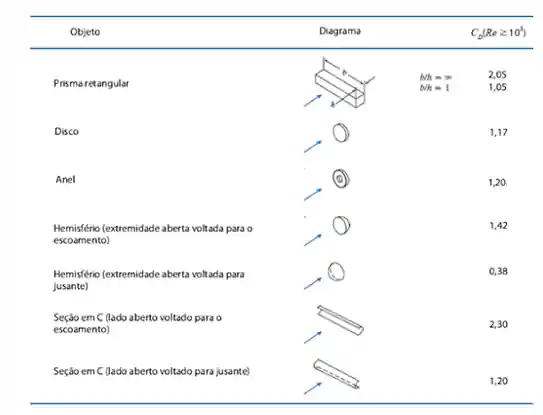
Essa tabela lista alguns tipos de geometria mais usuais, indicando os valores respectivos do coeficiente de atrito. Ela será bastante útil na resolução de exercícios envolvendo arrasto.
Agora que já entendemos um pouco mais sobre o arrasto, bora pros exercícios?
Coeficiente de Arrasto
Exercícios Resolvidos
Exercício Resolvido #1
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C. Introdução à Mecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
A componente vertical da velocidade de aterrissagem de um paraquedas deve ser inferior a . A massa total do paraquedas com o paraquedista é . Determine o mínimo diâmetro do paraquedas aberto.
Passo 1
Fala, galera! Vamos agora fazer um projeto e paraquedas, pra não cair de cara na prova. Ahah
Bom, antes de começarmos a calcular qualquer coisa do problema, precisamos entender bem a situação. O enunciado traz um sistema composto por paraquedista e seu paraquedas (cuja massa é conhecida e igual a ).
Sabemos que na queda, além da força peso (), também verificamos a força de arrasto () causada pelo ar, como observamos abaixo:
Nessa situação, consideramos o paraquedas como um hemisfério (com extremidade aberta – côncava – para o escoamento), cujo diâmetro precisamos determinar.
Como a velocidade da queda é constante (), podemos considerar que o movimento é uniforme e, portanto, a soma das forças deve ser igual a zero.
Passo 2
Vamos, então, calcular as forças envolvidas! O peso () será igual a:
Já a força de arrasto () é dada pela expressão:
Para esse tipo de geometria, vemos na tabela que o coeficiente de arrasto () é dado por:
Já sabemos a densidade do ar () e a velocidade (), logo a área é nossa única incógnita. Como as forças se anulam, podemos escrever que:
Isolando a área:
E substituindo essa galera:
OBS: Note que avaliar o sistema paraquedista-paraquedas em movimento descendente (pra baixo) no ar “parado” é equivalente a avaliar o sistema paraquedista-paraquedas parado e o ar em movimento ascendente (pra cima). Isso está atrelado ao conceito físico de velocidade relativa.
Passo 3
A escolha da área nesse momento é um ponto crucial. Qual área vamos utilizar?
Você poderia pensar o seguinte: “Bom, a área de um hemisfério é metade da área e uma esfera, então eu jogo essa expressão!”. Pois é, mas daria errado! Mas por quê?
A área que interessa é somente a área perpendicular ao escoamento. Esse pensamento é análogo ao que fazemos para calcular a pressão sobre uma área não-uniforme, nós só pegamos a componente normal à força.
Se considerássemos a componente paralela, estaríamos avaliando o movimento lateral do paraquedas, ou seja, se ele estaria indo para a esquerda ou direita. Como estamos interessados no movimento vertical (queda), só é importante pra gente a área da projeção ilustrada na imagem abaixo:
Temos que o diâmetro do círculo na projeção é o mesmo diâmetro do paraquedas. Portanto, podemos escrever:
OBS: Sempre aproximaremos o diâmetro “para cima”, pois sabemos que mantidas as demais condições, quanto maior o diâmetro, maior será a área do paraquedas e, consequentemente, maior será a força de arrasto. Se fosse menor que esse diâmetro, observaríamos que: .
Resposta
Exercício Resolvido #2
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C. Introdução à Mecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
Um rebocador de barcaças fluviais é testado em um tanque de provas. O modelo do rebocador é construído em uma razão de escala de 1:13,5. As dimensões do modelo são: comprimento total 3,5 m, través 1 m e calado 0,2 m. (O deslocamento do modelo em água doce é 5500 N.) Estime o comprimento médio da superfície molhada do casco. Calcule a força de arrasto de atrito superficial no protótipo a uma velocidade de 3,601 m/s com relação à água.
Dica: Assuma o rebocador como um paralelepípedo de dimensões 3,5 m:1,0 m:0,2 m.
Passo 1
Para simplificar, vamos assumir que o rebocador é um paralelepípedo.
Sabemos o comprimento total do sistema (), mas para encontrarmos o comprimento submerso do protótipo do rebocador, podemos utilizar o conceito de empuxo.
Como o rebocador boia, o resultado das forças que empurram ele pra cima e que empurram ele pra baixo tem que ser iguais.
Pra baixo a gente tem o próprio peso do rebocador. Pra cima, temos o empuxo.
E o módulo do empuxo é dado por:
O volume é a multiplicação das três dimensões:
Passo 2
Se a proporção com o protótipo e o real é de, teremos o equivalente na geometria do rebocador real equivalente a:
Passo 3
Nós vimos que o coeficiente de arrasto () pode ser expresso por:
Sabemos ainda que existem expressões para o cálculo de em cada faixa de , então vamos inicialmente calcular o número de Reynolds para sabermos qual expressão é a mais adequada para este escoamento:
Assim concluímos que o coeficiente de arrasto () pode ser calculado por:
A área pode ser calculada por:
Portanto:
Resposta
Exercício Resolvido #3
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C. Introdução à Mecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
Um misturador rotativo é construído com dois discos circulares, conforme mostrado. O misturador é acionado a dentro de um grande vaso contendo uma solução de salmoura (). Despreze o arrasto sobre as hastes e o movimento induzido no líquido. Estime o torque e a potência mínimos requeridos para acionar o misturador.
OBS: A sigla significa “specific gravity” e se refere a densidade relativa da substância, ou seja, a razão entre a densidade da substância sobre a densidade da água.
Passo 1
Vamos pensar um pouco na nossa estratégia de cálculo?
O enunciado nos pede para calcular o torque e a potência requerida para que o misturador possa operar. Ambos são funções da força a qual o fluido é submetido, então precisamos calcular essa força.
Diz aí: qual o nome dessa força? Isso mesmo! A força de arrasto! Como já vimos, a força de arrasto () pode ser expressa por:
Vamos, então, encontrar os parâmetros a serem determinados começando pela área do disco (:
A velocidade linear ( é dada por:
Nós já vimos que existem valores tabelados para o coeficiente de arrasto () de geometrias específicas, inclusive para um disco, desde que .
Então, bora verificar o número de Reynolds desse escoamento. Vamos utilizar como comprimento característico o diâmetro do disco e já sabemos a densidade da salmoura:
Ótimo! Podemos usar o valor da tabela!
Pela tabela, o coeficiente de arrasto para um disco é dado por:
Dessa maneira, é possível calcularmos a força de arrasto ():
OBS: A densidade é , pois a definição de densidade relativa () é dada por:
Passo 2
Sabemos que o torque () é dado pelo produto entre a força aplicada e a distância do eixo de rotação, logo:
Assim, conseguimos calcular a potência mínima requerida () para acionar o misturador:
Resposta
Exercício Resolvido #4
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C.Introdução àMecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
Você é um engenheiro recém-formado e decide fazer com que um misturador rotativo seja melhorado por meio da substituição dos discos por anéis. Os anéis podem ter a vantagem adicional de fazer com que o misturador misture mais eficientemente. Se o misturador absorve 350 W a 60 rpm, refaça o projeto. Existe uma restrição no projeto de que o diâmetro externo dos anéis não deve exceder 125 mm.
Passo 1
Agora a estratégia é outra, padawan! Temos uma potência fixada e queremos projetar um misturador rotativo com anéis (e não mais discos, como no anterior).
Sabemos que a potência () é função do torque e pode ser descrita como:
Como o torque () é dado pelo produto entre a força aplicada e a distância ao eixo, temos que a força de arrasto será dada por:
Passo 2
Lembra da equação que descreve a força de arrasto? Podemos expressá-la como:
Observe que os termos , e independem do raio interno do anel, então já podemos determiná-los.
O coeficiente de arrasto () é função do tipo de geometria do sistema. Pela tabela, temos que o para objetos anulares é dado por:
Além disso, a velocidade linear ( é dada por:
Dessa forma, a única variável a ser determinada é a área do anel ():
Passo 3
Como a área é função dos diâmetros interno e externo do anel e nos foi informado que o anel tem diâmetro externo máximo de , podemos escrever a área como função somente do diâmetro interno:
Assim:
Resposta
Exercício Resolvido #5
FOX, R. W.; MCDONALD, A. T.; PRITCHARD, P.J.; LEYLEGIAN, J. C.Introdução àMecânica dos Fluidos, 8ª ed. Minas Gerais: Gen LTC, 2011.
A resistência ao movimento de uma boa bicicleta sobre um pavimento liso é decorrente, quase que inteiramente, do arrasto aerodinâmico. Considere que a massa total de ciclista e bicicleta é . A área frontal, medida de uma fotografia, é . Experiências em uma colina com declive de 9% mostram que a velocidade terminal é A partir desses dados, o coeficiente de arrasto é estimado como . Verifique os cálculos do coeficiente de arrasto. Estime a distância necessária para que o ciclista e bicicleta desacelerem de para , enquanto o ciclista descansa nos pedais após atingir o piso plano.
Passo 1
Aqui a geometria do sistema não se enquadra em nenhum tipo tabelado, pode conferir que não tem “bicicleta” naqueles tipos de geometria da tabela ahah
Bom, então, como saber o coeficiente de arrasto? Nesse problema o enunciado nos fornece somente uma estimativa para seu valor () e nos pede para verificar. Então, o coeficiente será exatamente nossa incógnita e, portanto, precisamos encontrar a equação que rege o fenômeno e determinar os demais parâmetros.
O sistema avaliado consiste no conjunto ciclista-bicicleta como encontramos na imagem abaixo:
Lembra das aulas de física de plano inclinado? Pois é, vamos utilizar decompor aqui as forças que atuam no nosso “bloquinho”:
Já sabemos os valores de: e . Agora, precisamos encontrar o valor de , a fim de determinarmos a componente peso na direção .
Foi informado que a declividade do plano é de , portanto, podemos relacioná-la com a tangente do ângulo da seguinte forma:
Dessa maneira, já temos todos os parâmetros para o cálculo de :
Esse foi o valor calculado, vamos comparar com a estimativa inicial. O erro relativo da estimativa em relação ao cálculo é de:
Erros superiores a 10% geralmente não são aceitos, mas numa visão menos conservadora, poderíamos assumir o valor como satisfatório.
Passo 2
Agora é a parte do enunciado! Vamos calcular a distância necessária para que o ciclista sofra uma desaceleração de para . A força resultante sobre um corpo é dada por:
Como o enunciado afirma que a resistência ao movimento é quase que interiamente devido à força de arrasto, temos que:
Como estamos interessados na distância para que haja a desaceleração (e não no tempo), podemos reescrever a velocidade como sendo:
Com a notação de Leibniz, podemos substituir o infinitesimal na equação da força resultante:
Integrando a equação, teremos:
Utilizando o coeficiente de arrasto () estimado:
Resposta
CONFERIR RESOLUÇÃO! VERIFICAR SE A FORÇA RESULTANTE NÃO DEVERIA SER A COMPONENTE DO PESO EM X MENOS A FORÇA DE ARRASTO!
Exercício Resolvido #6
Exame Nacional de Desempenho dos Estudantes – ENADE – Engenharia Grupo III –2011Fox, R.W., McDonald, A. T., Pritchard, P. Introduction to Fluid Mechanics. 6 ed New York: Willey International, 2004, p.787 (com adaptações)
O coeficiente de arrasto de um disco com um escoamento normal a uma de suas faces é Cd = 1,17, para valores do número de Reynolds maiores do que 1000.
Em um experimento tem-se água escoando normal à face de um disco. A força de arraste da água no disco é de alguma forma determinada. Repete-se o experimento com duas modificações, utiliza-se ar como fluido e altera-se a velocidade do escoamento para garantir que nos dois experimentos o número de Reynolds seja o mesmo e superior a 1000. A força de arraste do ar no disco é, também, de alguma forma determinada. Considere que a água com e , e considere o ar com e .
Com relação às forças que atuam nesse experimento, é correto afirmar que
(A) A força de arrasto será a mesma nos dois experimentos, pois o número de Reynolds e o coeficiente de arrasto são os mesmos; e a força de empuxo será maior no experimento com água.
(B) A força de arrasto será maior no experimento com água, no qual a velocidade do fluido é menor; e a força de empuxo é maior no experimento com água.
(C) A força de arrasto será maior no experimento com água, no qual a velocidade do fluido é menor; e a força de empuxo será menor no experimento com água.
(D) A força de arrasto será maior no experimento com água, no qual a velocidade do fluido é maior; e a força de empuxo é maior no experimento com água.
(E) A força de arrasto será menor no experimento com água, no qual a velocidade do fluido é maior; e a força de empuxo será menor no experimento com água.
Passo 1
E aí! Para resolver essa questão vamos responder duas perguntas:
“A força de arrasto na água é maior, menor ou igual à força de arrasto no ar?”
“O empuxo no experimento com a água é maior, menor ou igual ao empuxo do ar?”
Começando pela força de arrasto
Nos dois experimentos temos o mesmo objeto, logo, temos a mesma área projetada e o mesmo coeficiente de arrasto , pois ele foi definido pela geometria como confirma a primeira frase da questão (que diz quanto vale o para um disco)
Deixando quem não varia em evidência
Mas, de um experimento para o outro, muda a massa específica do fluido e a velocidade.
A velocidade muda de tal forma que o Reynolds é o mesmo nos dois experimentos. Vamos calcular essa mudança
Então, isolando a velocidade:
Substituindo essa expressão no cálculo da força de arrasto
Rearrumando e colocando entre parênteses as variáveis que estão fixas
Agora sim, substituindo a viscosidade e massa específica da água
Substituindo a viscosidade e massa específica do ar
Comparando:
Logo, a força de arrasto é maior no experimento com água. Assim, as alternativas A e E estão erradas.
Passo 2
Além disso, as alternativas falam sobre a velocidade do fluido. Como obtivemos a partir do Reynolds, a velocidade é
Para a água
Para o ar
Então, a velocidade no experimento da água é 10 vezes menor que a do ar. E assim, alternativa D está errada.
Passo 3
Quanto ao Empuxo, vamos relembrar
A força de empuxo depende da massa específica do fluido, do volume submerso e da gravidade. Como o volume submerso e a gravidade são os mesmos nos 2 experimentos, vamos analisar
A massa específica da água é 1000 vezes maior que a do ar, portanto, o empuxo é maior no experimento com a água.
A alternativa que inclui essa resposta bem como a da força de arrasto e a da velocidade é a letra B!
Resposta
Letra B
Exercício Resolvido #7
Concurso Engenheiro Química Júnior – Companhia Paranaense de Energia COPEL - 2011
A força de arraste surge quando há escoamento de fluido ao redor de um corpo sólido. Um sólido em queda livre através de um fluido acelera até haver equilíbrio entre a força de arraste, o peso do sólido e o empuxo, sendo essa condição conhecida como condição terminal, e a velocidade, como velocidade terminal.
1. A força de arraste depende da densidade do fluido e independe da densidade do sólido.
2. A força de arraste sobre um sólido, na condição terminal, independe da forma do sólido, uma vez que o balanço de forças é sempre o mesmo.
3. A força de arraste é relacionada ao transporte de quantidade de movimento e influencia fortemente as operações unitárias de sedimentação, transporte pneumático e fluidização.
4. A força de arraste sobre uma esfera pode ser dividida em arraste de atrito e de pressão, sendo que as propriedades do fluido que mais influenciam cada uma delas são a viscosidade e a densidade, respectivamente.
Assinale a alternativa correta
a) Somente as afirmativas 1 e 3 são verdadeiras.
b) Somente as afirmativas 3 e 4 são verdadeiras.
c) Somente as afirmativas 2, 3 e 4 são verdadeiras.
d) Somente as afirmativas 2 e 4 são verdadeiras.
e) As afirmativas 1, 2, 3 e 4 são verdadeiras.
Passo 1
Fala, mestre! Para resolver essa questão, vamos fixar os conceitos que aprendemos na teoria
A força de arraste (ou de arrasto) é escrita assim:
A partir daí, já podemos concluir que ela depende da densidade do fluido apenas (ρ), o que mostra que a afirmação 1 é verdadeira:
“A força de arraste depende da densidade do fluido e independe da densidade do sólido” Certo!
Vamos analisar agora a afirmação 2: “A força de arraste sobre um sólido, na condição terminal, independe da forma do sólido, uma vez que o balanço de forças é sempre o mesmo”
Como o enunciado explica, na condição terminal há um equilíbrio de forças, ou seja, o somatório das forças é zero. Assim, a força de arrasto pode ser calculada a partir da força peso e empuxo, que independem da forma do objeto
Logo, a afirmação 2 está correta. :)
Mais uma! Vamos para a terceira: “A força de arraste é relacionada ao transporte de quantidade de movimento e influencia fortemente as operações unitárias de sedimentação, transporte pneumático e fluidização”
Vimos na teoria que a força de arrasto representa a componente paralela do escoamento. Se há escoamento, há transporte de quantidade de movimento. Então, eles estão relacionados.
Além disso, vimos que essa condição terminal vai ser importante em operações unitárias. Mas vamos focar em MecFlu por enquanto, ok? Hahaha
Com isso, a afirmação 3 está certinha tb!
Finalmente, chegamos na quarta: “A força de arraste sobre uma esfera pode ser dividida em arraste de atrito e de pressão, sendo que as propriedades do fluido que mais influenciam cada uma delas são a viscosidade e a densidade, respectivamente”
Siiim! A força de arraste é influenciada pelo arrasto de atrito e o de pressão. O arrasto de atrito é relacionado às forças viscosas na camada-limite e o arrasto de pressão se relaciona com as diferenças de pressão ao longo do escoamento.
Essas diferenças de pressão influenciam na massa específica do fluido e consequentemente em sua densidade. Logo, a afirmação 4 também está certa.
Como 1, 2, 3, e 4 são verdadeiras, a opção correta é a E!
Resposta
Letra E
Exercício Resolvido #8
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 515, ex. P 7.16
Uma placa plana fina de 55 cm por 110 cm está imersa em um fluxo de 6 m/s de óleo SAE 10 a 20°C. Calcule o arrasto total de atrito, caso o fluxo seja paralelo (a) ao lado maior ou (b) ao lado menor.
Dados: ,
Coeficiente de arrasto (placa plana, sem gradiente de pressão, laminar)
Coeficiente de arrasto (placa plana, sem gradiente de pressão, turbulento)
Escoamento Laminar:
Escoamento Turbulento:
Passo 1
Opa! Temos nesse exercício uma geometria diferente: uma placa plana fina. Além disso, vamos considerar que o arrasto de pressão é quase nulo. Assim, o arrasto total de atrito será o arrasto total, que vimos na teoria :D
Ué? Mas podemos considerar isso? Sim! Inclusive, os valores de coeficiente de arrasto dados são válido para arrasto viscoso sem gradiente de pressão.
Queremos saber então a força de arrasto
Conhecemos a massa específica e a velocidade. A área é duas vezes a área da placa, pois o escoamento está passando nos 2 lados dessa placa fina. Ficamos assim:
Para encontrar o coeficiente de arrasto, vamos utilizar uma das expressões fornecidas no enunciado. Uma serve para escoamento laminar e outra para turbulento. Vamos então calcular Reynolds para o escoamento sobre a placa:
L é o comprimento paralelo ao escoamento. Na letra a, o exercício pediu para considerar que o fluxo fosse paralelo ao lado maior. Nesse caso, L = 110 cm = 1,1 m. Substituindo
O enunciado deu a referência de escoamento laminar como . Logo, esse é um escoamento laminar. Por isso, vamos usar essa fórmula do coeficiente de arrasto
Assim, vamos calcular a força de arrasto
Essa é a força de arrasto considerando o fluxo de fluido paralelo ao lado maior.
Passo 2
Agora vamos calcular a força de arrasto considerando o fluxo paralelo ao lado menor. Para isso, precisamos verificar se o escoamento é laminar ou turbulento nesse caso. Agora com L = 0,55 m calculamos Reynolds
Então, o escoamento é laminar nesse caso também. Assim, utilizamos a mesma fórmula para calcular o coeficiente de arrasto
Por fim, vamos calcular a força de arrasto
E essa é a força de arrasto considerando o fluxo de fluido paralelo ao lado menor. O valor dela é maior que o calculado para o lado maior. Ou seja, a direção do fluxo na placa influencia na força de arrasto!
Resposta
a)
b)