Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Escoamento Laminar e Turbulento

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos trocar uma ideia sobre sobre escoamentos laminar e turbulento, bem como algumas equações que podemos usar para caracterizar cada um desses regimes.

Bora lá entender um pouquinho melhor?

👇 Não deixe de conferir a sequência desse conteúdo 👇

Regimes de Escoamento em Dutos: Laminar e Turbulento

Antes de mais nada, a gente tem que entender como se define cada tipo de escoamento, né?

Para isso, vamos olhar para a seguinte figura:

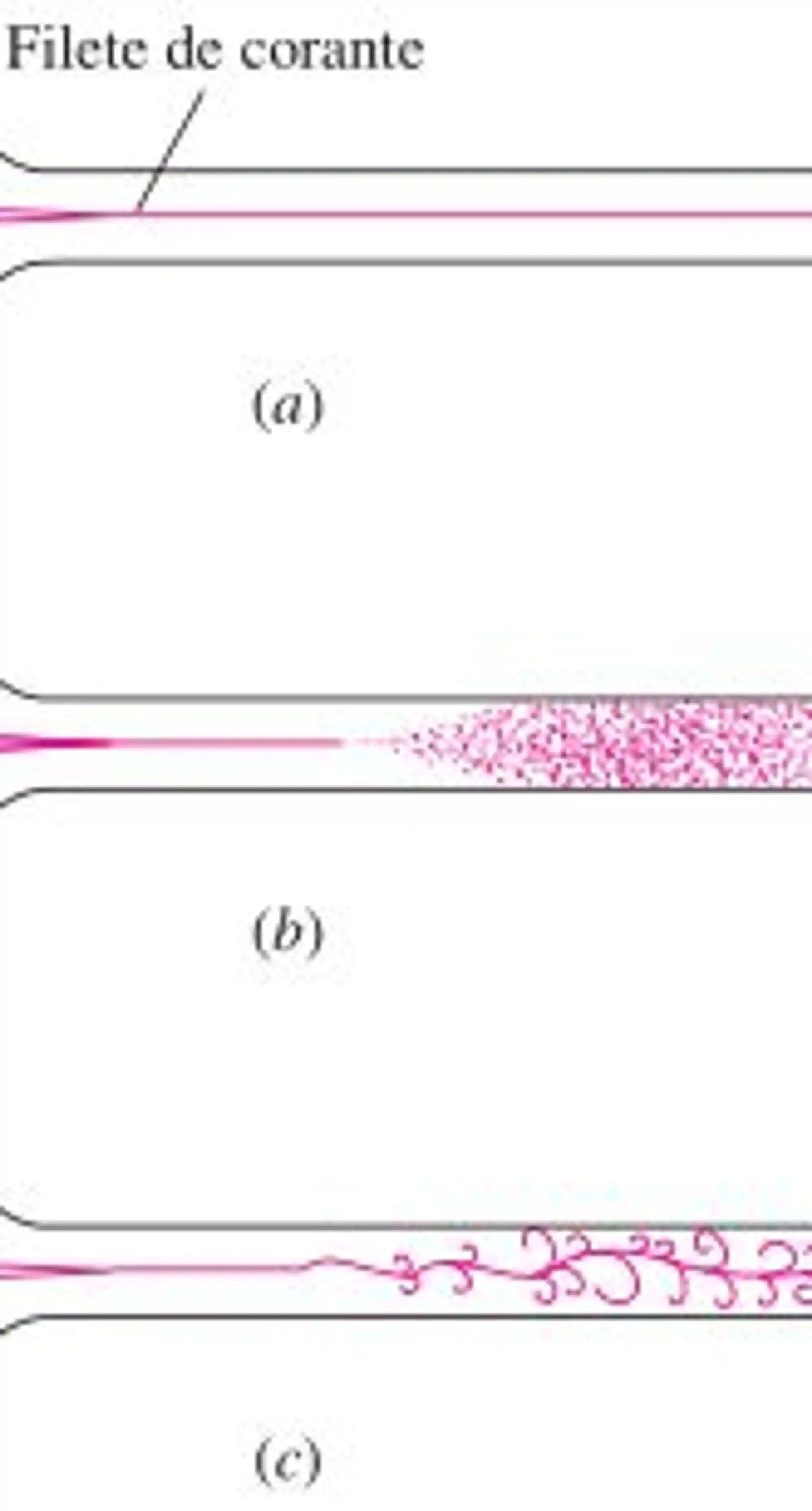
Ilustração: experimento de Reynolds.
Ilustração: experimento de Reynolds.

O que tá representado aí é o experimento feito por um tal de Osborne Reynolds. Esse cara colocou, em um tubo, água e um fluido colorido e observou diferentes padrões de escoamento conforme aumentava a velocidade dos fluidos.

Aquele primeiro ali representa o escoamento laminar. Ele é caracterizado pelo movimento em camadas (ou lâminas) dos fluidos. Repare como há pouca ou nenhuma mistura entre as diferentes camadas de fluido.

O próximo representa o escoamento turbulento. Ele ocorre quando há um aumento da velocidade de escoamento. Aqui, as partículas do fluido se comportam de maneira desordenada.

A última figura corresponde a um estado instantâneo do escoamento turbulento. Percebe como as partículas do corante apresentam movimento todo bagunçado? Às vezes elas vão pra trás, às vezes começam a rodar.

Beleza, então a gente já sabe que o tipo de escoamento depende da velocidade, será que depende de mais alguma coisa?

Número de Reynolds

O número de Reynolds fornece um parâmetro para caracterizar o tipo de um escoamento. Ele é expresso assim:

👉 é a massa específica do fluido.

👉 é a viscosidade dinâmica.

👉 é a velocidade no centro do escoamento.

👉 é o diâmetro do duto.

Quando fazemos os cálculos, se , consideramos o escoamento como laminar. Qualquer valor acima é um escoamento em transição para a turbulência ou já turbulento.

Só que é o seguinte, os valores de referência podem variar dependendo de pra quem você pergunta, viu? Então fica ligado no que o seu professor usa durante as aulas.

Perda de Carga

Em qualquer tipo de escoamento, existem forças dissipativas, como o atrito com as superfícies do tubo ou a própria turbulência, concorda? Isso faz com que haja uma dissipação de energia do escoamento.

Essa perda de energia é chamada de perda de carga. Algumas vezes pode ser chamada também de queda de pressão, já que essa é uma consequência da redução de energia do fluido.

Matematicamente, a perda de carga é dada pela seguinte fórmula:

👉 é o fator de atrito.

👉 é o comprimento do duto.

👉 é o diâmetro do duto.

👉 é a velocidade de escoamento.

👉 é a aceleração da gravidade.

Fator de Atrito

O fator de atrito relaciona o número de Reynolds à rugosidade da parede.

Para o escoamento laminar, ele é dado por:

Mais pra frente, veremos outra expressão que vai ser usada para calcular esse fator para escoamentos turbulentos.

Por enquanto, isso é tudo que você precisa saber. Bora praticar com alguns exercícios!

Perda de Carga

Exercícios Resolvidos

Exercício Resolvido #1

Para o escoamento de óleo S A E   30 por um tubo de 5   c m de diâmetro, Figura A.1, para qual vazão em m 3 / h devemos esperar transição para a turbulência a a   20 ℃ e b   100 ℃ ?

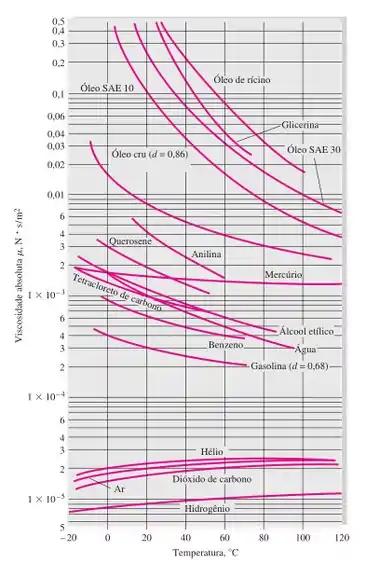
Figura 1. Viscosidade absoluta de fluidos comuns a 1 atm.

Passo 1

Nesse exercício devemos aplicar aquele número de Reynolds R e d = 2300 , que caracteriza a transição do escoamento laminar para o turbulento, lembra?

Sabemos que:

R e d = ρ V d μ

Do gráfico encontramos o valor de μ :

μ 20 ℃ = 0,25   N . s / m ²

μ 100 ℃ = 0,01   N . s / m ²

Olhando valores tabelados de massa específica:

ρ = 891   k g / m ³

O enunciado ainda fornece o valor do diâmetro:

d = 5   c m = 0,05   m

Passo 2

Substituindo na expressão de R e d , para 20 ℃ :

R e d = ρ V d μ

2300 = 891 . V . ( 0,05 ) ( 0,25 )

V = 12,91   m / s

Para 100 ℃ :

R e d = ρ V d μ

2300 = 891 . V . ( 0,05 ) ( 0,01 )

V = 0,52   m / s

Passo 3

Substituindo na fórmula da vazão Q = V A , sendo A = π d ² 4

20 ℃ :

Q = V A

Q = 12,91 . π ( 0,05 ) ² 4

Q = 0,025 m 3 s = 91,25 m 3 h

100 ℃ :

Q = V A

Q = ( 0,52 ) . π 0,05 2 4  

Q = 1,02 . 10 - 3 m 3 s = 3,68 m 3 h

Resposta

Letra a)

Q = 91,25 m 3 h

Letra b)

Q = 3,68 m 3 h

Exercício Resolvido #2

Água a 20 ℃ escoa por um tubo inclinado de 8   c m de diâmetro. Nas seções A e B são obtidos os seguintes dados: p A = 186   k P a , V A = 3,2   m / s , z A = 24,5   m , p B = 260   k P a , V B = 3,2   m / s e z B = 9,1   m . Qual é o sentido do escoamento? Qual é a perda de carga em metros?

Passo 1

Podemos ver que o enunciado nos dá as propriedades em dois pontos do tubo A e B , com as seguintes propriedades:

A p A = 186   k P a = 186000   P a V A = 3,2   m / s z A = 24,5   m

B p B = 260   k P a = 260000   P a V B = 3,2   m / s z B = 9,1   m

Além disso o fluido é água, logo a massa específica é ρ = 1000   k g / m ³

Passo 2

Para determinarmos o sentido do escoamento vamos comparar cada lado da Equação da Energia:

p A ρ g + V A ² 2 g + z A = p B ρ g + V B ² 2 g + z B + h p

Como V A = V B os termos de velocidade de ambos os lados se cancelam:

p A ρ g + z A = p B ρ g + z B + h p

186000 1000 × 9,81 + 24,5 = 260000 1000 × 9,81 + 9,1 + h p

43,5 = 35,6 + h p

Podemos dizer que o fluido vai de A → B , pois há mais carga ou pressão em A .

Passo 3

Para calcularmos o fator de perda de carga basta terminarmos de resolver a expressão do Passo 2:

43,5 = 35,6 + h p

h p = 7,9   m

Resposta

Escoamento vai de A → B e   h p = 7,9   m .

Exercício Resolvido #3

Um canudo para refrigerante tem 20   c m de comprimento e 2   m m de diâmetro. Ele fornece refrigerante gelado, aproximado como água a 10 ° C , à taxa de 3   c m 3 / s . (a) Qual é a perda de carga através do canudo? Qual é o gradiente de pressão axial ∂ p / ∂ x se o escoamento é (b) verticalmente para cima ou (c) horizontal? O pulmão humano pode fornecer tanta vazão?

Passo 1

Outro exercício que temos um duto/canudo com escoamento viscoso.

Temos as seguintes informações do enunciado:

L = 20   c m = 0,20   m

d = 2   m m = 0,002   m

Q = 3 c m 3 s = 3 × 10 - 6 m 3 s

ρ á g u a 10 ℃ = 1000 k g m 3

μ á g u a 10 ℃ = 1,307 × 10 - 3   N . s m 2

Passo 2

Devemos agora calcular a perda de carga da água passando pelo canudo:

h p = f L d V ² 2 g

Desta fórmula não conhecemos V nem f .

Podemos calcular V a partir da vazão Q e da área A = π d 2 4 = 3,14 × 10 - 6   m ²

V = Q A

V = 3 × 10 - 6 3,14 × 10 - 6

V = 0,96 m s

Calculamos então o fator de atrito f :

f = 64 R e d = 64 ρ V d μ

f = 64 1000 × 0,96 × 0,002 1,307 × 10 - 3

f = 0,0436

Substituindo em h p : h p = f L d V ² 2 g

h p = ( 0,0436 ) × 0,2 0,002 × ( 0,96 ) ² ( 2 × 9,81 )

h p = 0,2   m

Passo 3

Usando a equação da Energia no caso b vertical, com fluxo para cima, sendo de 1 → 2 :

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

Podemos supor que z 1 = 0 , z 2 = L que dependem do nosso referencial;

Que V 1 = V 2 ;

Substituindo,

p 1 ρ g = p 2 ρ g + L + h p

Podemos multiplicar ambos os lados por ρ g :

p 1 = p 2 + ρ g ( L + h p )

p 1 - p 2 = ρ g ( L + h p )

O enunciado nos pede ∂ p ∂ x , que podemos aproximar por

Δ p L = p 1 - p 2 L

Substituindo na equação, ou seja, dividindo ambos lados por L :

p 1 - p 2 L = ρ g L ( L + h p )

Δ p L = ρ g L L + h p

Δ p L = 1000 × 9,81 0,2 0,2 + 0,2

Δ p L = 19620 P a m

Passo 4

Realizando o mesmo procedimento do Passo 3, mas agora com z 1 = z 2 = 0 :

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

p 1 ρ g = p 2 ρ g + h p

p 1 - p 2 ρ g = h p

Dividindo por L :

p 1 - p 2 L = ρ g h p L

Δ p L = 1000 × 9,81 × 0,2 0,2

Δ p L = 9810 P a m

Resposta

Letra a)

h p = 0,2   m

Letra b)

Δ p L = 19620 P a m

Letra c)

Δ p L = 9810 P a m

Exercício Resolvido #4

A fim de determinar a viscosidade de um líquido de densidade 0,95, você preenche, a uma profundidade de 12 cm, um grande recipiente com drenagem por um tubo vertical de 30 cm de comprimento fixado ao fundo. O diâmetro do tubo é 2 mm, e a taxa de drenagem é 1,9 cm³/s. Qual é o valor da viscosidade do fluido? O escoamento no tubo é laminar?

Passo 1

Neste exercício não temos uma imagem para nos ajudar, portanto vamos esquematizar o problema.

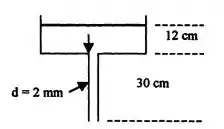
A superfície de entrada é a do topo do tanque e a de saída o tubo final.

Isso nos dá os seguintes valores de entrada e saída que usaremos na nossa equação da energia:

e n t r a d a V 1 = 0 z 1 = 42   c m p 1 = 0

Mas por quê V 1 = 0 ?

Isso é válido para qualquer superfície de controle que apesar de ter uma vazão Q , temo uma área A 1 tão grande que a velocidade que a superfície se move é desprezível.

No caso de p 1 = 0 , estamos trabalhando com pressão manométrica e não a absoluta. Caso fossemos trabalhar com a absoluta utilizaríamos a pressão atmosférica.

Para a sáida temos:

s a í d a V 2 = Q / A 2 z 2 = 0 p 2 = 0

Um líquido ter densidade   0,95 significa:

ρ l í q u i d o ρ á g u a = 0,95

Supondo que ρ á g u a = 1000 k g m 3

ρ l í q u i d o = 950   k g / m ³

Passo 2

Vamos então calcular V 2 = Q / A 2 e substituir os valores do Passo 1, na equação da energia:

V 2 = Q / A 2

V 2 = Q π d ² 4

V 2 = 4 1,9 × 10 - 6 π 2 × 10 - 3 ²

V 2 = 0,605   m / s

Dada a equação da energia:

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

Substituímos o que já conhecêmos:

0 + 0 + 0,42   m = 0 + 0,605 ² 2 × 9,81 + 0 + h p

Logo,

h p = 0,42 - 0,605 ² 2 × 9,81

h p = 0,4   m

Passo 3

Devemos lembrar da expressão da perda de carga

h p = f L d V ² 2 g

Em que,

f = 64 R e d = 64 ρ V d μ

Como não sabemos se o escoamento é laminar ou não vamos calcular o número de Reynolds, que deve ser menor que 2300 no caso laminar:

R e d = ρ V d μ

R e d = 950 × 0,605 × 0,002 μ < 2300

Logo,

μ > 950 × 0,605 × 0,002 2300

μ > 5 × 10 - 4   k g / ( m . s )

Curiosamente quase todos líquidos se encontram acima deste valor de viscosidade. Normalmente, apenas gases tem viscosidades menores que este valor. Portanto para quase todo líquido este escoamento é laminar.

Obs: Isso não é uma informação que você devia ter nascido junto, fica tranquilo. Mas é bom a gente começar a entender as ordens de grandeza de viscosidade. Gases são 10 - 5 , líquidos 10 - 3 , mais ou menos em torno disso.

Portanto podemos utilizar a expressão que conhecemos para o fator de atrito:

f = 64 R e d

Substituindo na expressão da perda de carga:

h p = 64 R e d L d V ² 2 g

h p = 64 μ ρ V d L d V ² 2 g

Rearranjando em função de μ :

μ = h p ρ g d ² 32 V L

Substituindo os valores, sendo L = 30   c m = 0,3   m :

μ = 0,4 × 950 × 9,81 × ( 0,002 ) ² 32 × 0,605 × 0,3

μ = 2,57 × 10 - 3   k g / ( m . s )

Como já tinhamos hipotetizado o escoamento como sendo laminar, confirmamos a hipóstese:

μ > 5 × 10 - 4   k g / ( m . s )

2,57 × 10 - 3 > 5 × 10 - 4   k g / ( m . s )

Escoamento laminar.

Resposta

μ = 2,57 × 10 - 3   k g / ( m . s )

Escoamento é laminar.

Exercício Resolvido #5

Uma compressão constante sobre o pistão na Figura produz uma vazão Q = 0,15   c m 3 / s através da agulha. O fluido tem ρ = 900   k g / m 3 e μ = 0,002   k g / ( m ∙ s ) . Qual a força F   necessária para manter o escoamento?

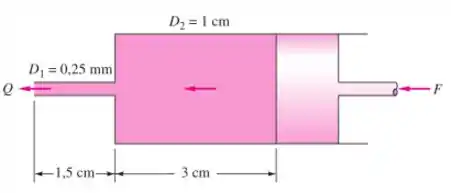
Passo 1

Então galera, mais uma vez aplicaremos a equação da energia e veremos o que nos falta para resolver o problema:

p 1 ρ g + V 1 ² 2 g + z 1 + h p = p 2 ρ g + V 2 ² 2 g + z 2

Neste caso a perda de carga fica do lado 1, pois é a “saída” do escoamento.

Podemos dizer que não há variação na altura dos cilíndros, logo z 1 = z 2 :

p 1 ρ g + V 1 ² 2 g = p 2 ρ g + V 2 ² 2 g + h p

Pela expressão Q = V A podemos encontrar quanto valem nossa velocidades em cada parte do escoamento:

V 1 = Q π D 1 ² 4

Passando Q e D 1 para o Sistema Internacional:

Q = 0,15 c m 3 s = 0,15 × 10 - 6 m 3 s

D 1 = 0,25   m m = 0,25 × 10 - 3   m

Substituindo na equação:

V 1 = Q π D 1 ² 4

V 1 = 0,15 × 10 - 6 π 0,25 × 10 - 3 ² 4

V 1 = 4 π 0,15 0,0625 10 - 6 10 - 6

V 1 = 9,6 π   m / s ≅ 3,06   m / s

Fazendo o mesmo para V 2 :

D 2 = 1   c m = 1 × 10 - 2   m

V 2 = Q π D 2 ² 4

V 2 = 0,15 × 10 - 6 π 1 × 10 - 2 ² 4

V 2 = 4 × 0,15 π 10 - 6 10 - 4

V 2 = 4 × 0,15 π 10 - 2

V 2 = 0,006 π ≅ 0,0019   m / s

Como V 2 ≪ V 1 , vamos supor que V 2 ≈ 0 , ficamos com a equação:

p 1 ρ g + V 1 ² 2 g + h p = p 2 ρ g

Passo 2

Calcularemos agora a perda de carga h p representada pela perda de carga no tubo menor 1 mais o a do tubo maior 2:

h p = f 1 L 1 D 1 V 1 ² 2 g + f 2 L 2 D 2 V 2 ² 2 g

Como V 2 = 0 :

h p = f 1 L 1 D 1 V 1 ² 2 g + 0

Verificamos se podemos usar o fator de atrito laminar:

R e d = ρ V 1 D 1 μ = 900 × 3,06 × 0,25 × 10 - 3 0,002 = 344,25 < 2300

Verificada a condição de laminaridade:

f 1 = 64 R e d = 64 ρ V 1 D 1 μ

Logo:

h p = 64 ρ V 1 D 1 μ L 1 D 1 V 1 ² 2 g

h p = 32 L 1 V 1 μ ρ g D 1 ²

Antes de substituirmos valores, vamos levar a expressão da energia:

p 1 ρ g + V 1 ² 2 g + h p = p 2 ρ g

Reescrevendo:

p 1 - p 2 ρ g = - V 1 2 2 g + 32 L 1 V 1 μ ρ g D 1 ²

Multiplicando por ρ g ambos os lados:

p 1 - p 2 = - ρ V 1 2 2 + 32 L 1 V 1 μ D 1 ²

Substituindo os valores conhecidos:

p 1 - p 2 = - 32 × 0,015 × 3,06 × 0,002 0,25 × 10 - 3 2 - 900 × 3,06 ² 2

p 1 - p 2 = - 51215,2   P a

Isso era esperado pois o escoamento vai de 2 para 1 e não o contrário, logo

p 2 - p 1 = 51215,2   P a

Passo 3

Agora para calcularmos a força F , lembraremos da expressão da pressão:

∆ p = F A

∆ p = p 2 - p 1

A = π D 2 ² 4

Logo

F = ∆ p A

F = p 2 - p 1 π D 2 ² 4

Substituindo os valores:

F = 51215,2 π 1 × 10 - 2 ² 4

F = 4,02   N

Resposta

F = 4,02   N

Exercício Resolvido #6

Óleo SAE 30 a 20 ° C escoa no tubo de 3   c m de diâmetro da Figura que está inclinado a 37 ° . Para as medidas de pressão mostradas, determine (a) se o escoamento é para cima ou pata baixo e (b) a vazão em m 3 / h .

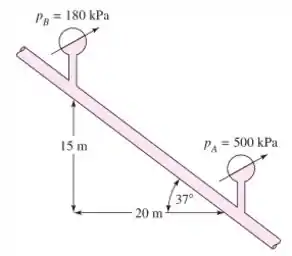
Passo 1

Fala pessoal, então nesse exercício a gente vai aplicar a equação da energia de novo, mas dessa vez vamos ficar atentos pra cada lado da equação, da entrada e saída.

A princípio não sabemos quem é entrada e quem é saída, então vamos supor que A seja a entrada do escoamento. Vem comigo!

Propriedades do óleo SAE 30 a 20 ℃ :

ρ = 891 k g m 3

μ = 0,29   k g / ( m . s )

Passo 2

Aplicamos a equação da energia:

p A ρ g + V A ² 2 g + z A = p B ρ g + V B ² 2 g + z B + h p

Valores que conhecemos pelo enunciado e pelo desenho:

p A = 500   k P a z A = 0 p B = 180   k P a z B = 15   m

Como não há mudança na seção transversal do duto, V A = V B . O que deixa nossa equação com a cara:

p A ρ g = p B ρ g + z B + h p

Como não conhcecemos h p :

h p = p A - p B ρ g - z B

Substituindo tudo:

h p = 500 × 10 3 - 180 × 10 3 891 × 9,81 - 15

h p = 21,61   m

Se a perda de carga é positiva isso quer dizer que nossa suposição inicial estava correta, o escoamento é de A até B ! Portanto é para cima.

Passo 3

Para determinarmos a vazão devemos conhecer a velocidade do escoamento e a área transversal do duto:

Q = V A

Comecemos pela área, que é circular:

A = π d ² 4

A = π 3 × 10 - 2 ² 4

A = 7,1 × 10 - 4   m ²

Para a velocidade, lembramos da expressão da perda de carga para o caso laminar:

h p = 32 L V μ ρ g d ²

Como queremos V :

V = ρ g d ² h p 32 L μ

Podemos calcular L , ou por Pitágoras ou por trigonometria, já que temos o ângulo de 37 ℃ , mas se olharmos bem temos um triângulo 3,4,5 ou no caso 15,20,25, logo

L = 25   m

Substituindo os valores conhecidos:

V = 891 × 9,81 × 0,03 ² × 21,61 32 × 25 × 0,29

V = 0,73   m / s

Substituindo na expressão da vazão:

Q = V A

Q = 0,73 × 7,1 × 10 - 4

Q = 5,18 × 10 - 4   m ³ / s

Para convertemos para m ³ / h basta multiplicarmos por 3600 :

Q = 1,86   m ³ / h

Resposta

Letra a) Escoamento é para cima

Letra b)

Q = 1,86   m ³ / h

Exercício Resolvido #7

Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 491, ex. 8.1

(Adaptada) Ar a 100°C entra em um duto circular de diâmetro 125 mm. Encontre a vazão volumétrica na qual o escoamento torna-se turbulento.

Dado: Viscosidade cinemática do ar a 100°

ν = 2,29 × 10 - 5 m 2 / s

Passo 1

E aiiií! Bora encontrar essa vazão! :D Para isso, vamos usar nosso amigo (nosso melhor amigo daqui para frente, eu diria!) Reynolds!

Repara uma palavra-chave no enunciado: “torna-se turbulento”

Para um escoamento se tornar turbulento, ele precisa estar naquele Reynolds crítico, ou seja, aquele número de Reynolds específico no qual abaixo dele, temos escoamento laminar e acima dele, escoamento turbulento

Vimos na teoria que esse número de Reynolds crítico em um tubo é 2300! Então nosso ponto de partida é esse:

R e = ρ V D μ = 2300

Se o fluido fosse a água, nós saberíamos a massa específica e a viscosidade, certo? Mas, nesse caso aqui se trata do ar a 100°C. Não faço a menor ideia desses valores para o ar nessa Temperatura. E agora, José?

Então! O enunciado nos informou a viscosidade cinemática, ou seja, essa amiga aqui

ν = μ ρ

Substituindo em Reynolds

R e = V D ν = 2300

Sabemos do enunciado, que o diâmetro é 125 mm. Passando para o Sistema Internacional, são 0,125 m. Substituindo os valores do enunciado:

V × 0,125 2,29 × 10 - 5 = 2300

Fazendo as contas na calculadora

V = 0,42   m / s  

Passo 2

Beleza! Encontramos a velocidade. Mas o enunciado pede a vazão, certo? Lembrando quem é a vazão volumétrica

Q = V . A

Como a área é a área do tubo, que é π D 2 / 4

Q = V π D 2 4

Substituindo os valores no Sistema Internacional:

Q = 0,42 π 0,125 2 4

Q = 5,2 × 10 - 3   m 3 / s

E assim Reynolds nos ajudou a calcular a vazão volumétrica pedida! Bora para o próximo exercício? o/

Resposta

Q = 5,2 × 10 - 3   m 3 / s

Exercício Resolvido #8

Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 492, ex. 8.4

(Adaptada) Para escoamento em tubos circulares, a transição para escoamento turbulento ocorre usualmente em torno de R e   ≈ 2300 . Investigue a condição sob a qual os escoamentos de (a) ar-padrão e (b) água a 15°C tornam-se turbulentos em um tubo de 0,05 m de diâmetro.

Dados: Massas específicas

ρ á g u a ,   15 ° = 999   k g / m 3 ρ a r ,   15 ° = 1,23   k g / m 3

Viscosidade dinâmica

μ á g u a ,   15 ° = 1,002 × 10 - 3   P a . s μ a r ,   15 ° =   0,018 × 10 - 3 P a . s

Passo 1

Fala! Vamos investigar esse momento crítico, quando o escoamento se torna turbulento. O enunciado deu a dica logo ali no começo. Nessa situação, temos:

R e   ≈ 2300

Lembrando que Reynolds é esse carinha aqui

R e = ρ V D μ

Beleza! Então agora vamos analisar cada fluido separadamente. Vamos começar com o ar, que é a letra a.

A massa específica ρ e a viscosidade dinâmica μ do ar foram dados no final do enunciado. Substituindo

R e = 1,23 × V a r × 0,05 0,018 × 10 - 3

2300 = 68333,3 . V a r . 0,05

V a r = 0,67 3   m / s

Passo 2

E para a água? Qual seria essa condição? Ou seja: qual seria a velocidade para qual o escoamento num tubo de 0,05 m se tornaria turbulento?

De novo, Reynolds vai nos ajudar, só que agora vamos utilizar os valores de massa específica e viscosidade dinâmica para a água

R e = ρ V D μ

2300 = 999 × V á g u a × 0,05 1,002 × 10 - 3

V á g u a = 0,0 46   m / s

E assim, encontramos a velocidade da água nas condições pedidas 😊

Resposta

a) V a r = 0,673   m / s

b) V á g u a = 0,046   m / s

Exercícios de Livros Relacionados

Óleo SAE 10 a 20°C escoa pelo tubo vertical de 4 cm de diâmetro da figura abaixo. Para a leitura h = 42 cm do manômetro de mercúrio mostrado, (a) calcule a vazão volumétrica em m³/h e (b) determine o
Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145
Um viscosímetro capilar mede o tempo necessário para que um volume especificado v de líquido escoe por um tubo de vidro de pequeno diâmetro, como na figura a seguir. Esse tempo de trânsito é então cor
Para a configuração mostrada abaixo, o fluido é álcool etílico a 20°C, e os reservatórios são muito grandes. Determine a vazão que ocorre em m³/h. O escoamento é laminar?
Vamos resolver o problema P6.25 na forma literal usando a figura abaixo. Todos os parâmetros são constantes, exceto a profundidade Z(t) do reservatório. Determine uma expressão para a vazão Q ( t ) em