Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Diagrama de Moody

Ver Todos os Exercícios

Teoria

Fala aí! Vem com o RespondeAí conhecer o diagrama de Moody! 😉

Pra que serve o Diagrama de Moody?

O diagrama de Moody é um gráfico que relaciona o fator de atrito de Darcy com o número de Reynolds e a rugosidade relativa. Ele tem essa carinha aqui:

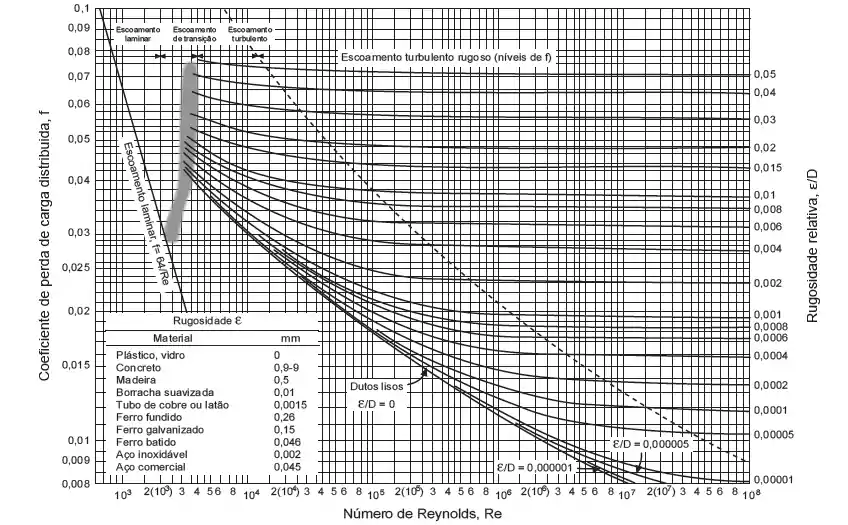
Diagrama de Moody
Diagrama de Moody

No diagrama acima, o Reynolds está representado no eixo horizontal, o fator de atrito no eixo vertical à esquerda e no eixo vertical à direta vemos a origem de diversas curvas, cada uma representando uma rugosidade relativa fixa em função do Reynolds.

Assustador, não é?! 😱

Mas a gente vai entender com calma o passo a passo de como ler o Diagrama de Moody pra utilizarmos nos nossos exercícios!

Agora o que a gente quer saber é: Afinal, qual é a função do Diagrama de Moody?

O Diagrama de Moody é útil para a estimação do fator de atrito de Darcy , a partir do número de Reynolds e uma rugosidade relativa , tanto para escoamentos laminares como para escoamentos turbulentos!

Agora sim, vamos aprender a usar o Diagrama de Moody!

Como Usar o Diagrama de Moody

A grande questão é: Como usar o diagrama de Moody para achar o fator de atrito, dado um Reynolds e uma rugosidade?

É o que vamos ver agora! Se liga nesse vídeo super completo que o Responde Aí preparou pra você aprender como usar o Diagrama de Moody de uma Vez por todas👇

Vamos fazer um exemplo junto com um passo a passo descomplicado.

Determine o fator de atrito para o fluxo de um fluido com e rugosidade relativa igual a .

PASSO 1: Calcular Re e ε/D

Nesse caso específico que estamos fazendo, o Reynolds e a rugosidade relativa já foram dadas, mas isso não é muito comum, normalmente você terá que calculá-los com outros dados que a questão fornece, beleza?

Nesse caso, usamos as fórmulas:

Onde é a velocidade de escoamento do fluido, é o diâmetro interno do tubo, e são a massa específica e viscosidade do fluido, respectivamente.

Já para calcular a rugosidade relativa só temos que dividir a rugosidade pelo diâmetro do tubo!

PASSO 2: Traçar no diagrama de Moody uma reta vertical com origem no ponto onde se encontra o valor de calculado

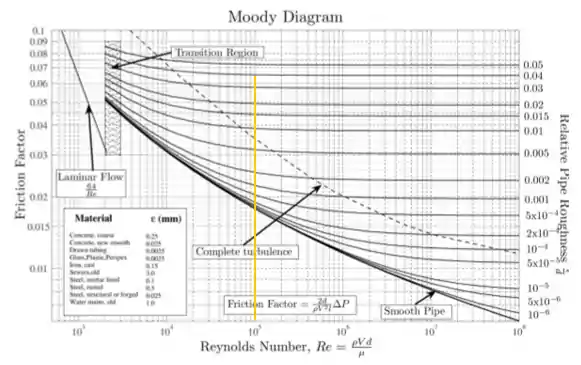
Marcação do número de Reynolds no diagrama de Moody
Marcação do número de Reynolds no diagrama de Moody

PASSO 3: Identificar a curva que tem a origem no valor da rugosidade relativa calculada.

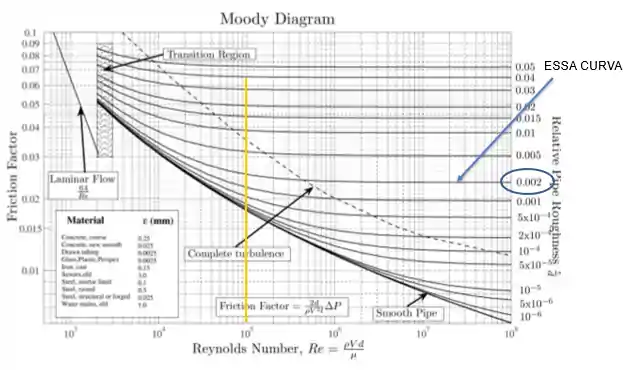
Identificação da curva correspondente ao valor de rugosidade relativa
Identificação da curva correspondente ao valor de rugosidade relativa

PASSO 4: Seguir a curva identificada no passo anterior até ela se encontrar com a reta vertical traçada no passo 2.

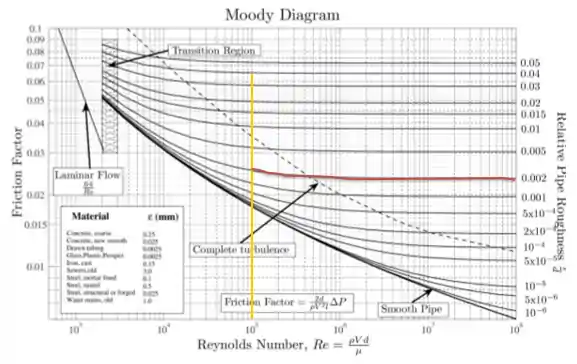
Representação do encontro da curva com a reta
Representação do encontro da curva com a reta

PASSO 5: Ler o valor da interseção das curvas traçadas

No ponto de encontro da curva com a reta trace uma reta horizontal para a esquerda, até o eixo do fator de atrito, e leia o valor como resposta.

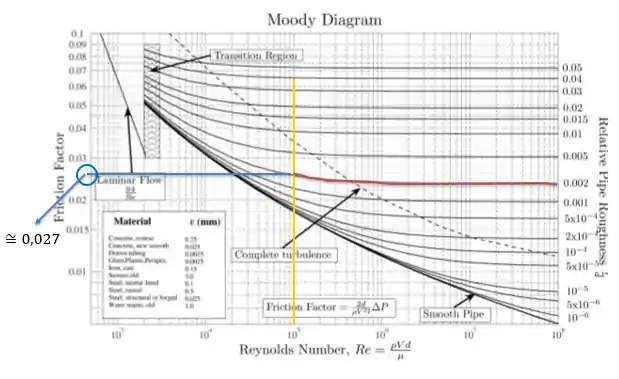
Leitura do valor do fator de atrito correspondente ao ponto de encontro da reta com a curva
Leitura do valor do fator de atrito correspondente ao ponto de encontro da reta com a curva

Sendo assim, para o nosso exemplo, o fator de atrito vale aproximadamente

Prontinho!

Tabela de Rugosidade

No exemplo que a gente fez ali em cima, o problema nos deu a rugosidade de mão beijada. Mas e se não fosse assim?!

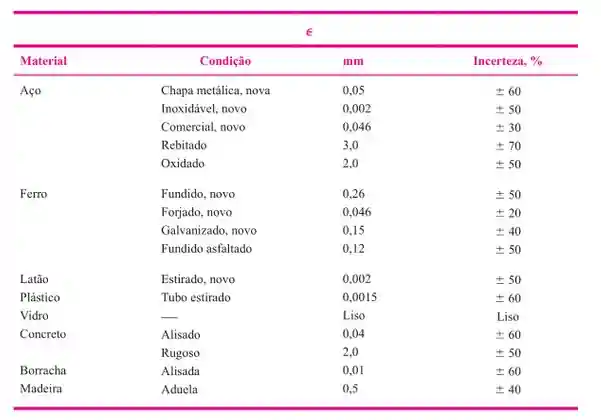
Nesse caso tudo o que você precisa fazer é consultar uma tabela de rugosidade, tipo essa daqui:

Tabela de Rugosidade
Tabela de Rugosidade

Equação de Moody

O diagrama de Moody é baseada em uma equação e ele torna tudo mais prático pra a gente. Mas, que equação é essa?!

Se liga na Equação de Moody:

Equação de Moody
Equação de Moody

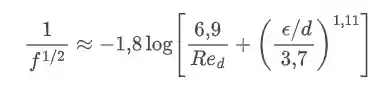
Mas é claro que é muito mais fácil usar o diagrama de Moody!

Agora partiu exercícios!!!!! :D

Tabela de Rugosidade

Equação de Moody

Exercícios Resolvidos

Exercício Resolvido #1

Mercúrio a 20 ° C escoa por 4   m de tubo de vidro de   7   m m   de diâmetro a uma velocidade média de 5   m / s . Calcule a perda de carga em metros e a queda de pressão em k P a .

Passo 1

Mais um problema de perda de carga, mas agora devemos ver em que faixa de Reynolds o escoamento se encontra e assim descobrirmos a perda de carga.

Para calcular R e d = ρ V d μ precisamos apenas das propriedades do mercúrio a 20 ℃ :

ρ = 13550 k g m 3

μ = 1,56 × 10 - 3   k g / ( m ∙ s )

Do enunciado:

V = 5 m s

d = 7   m m = 0,007   m

Logo

R e d = ρ V d μ = 13550 ∙ 5 ∙ 0,007 1,56 × 10 - 3

R e d = 304006

Como o tubo de vidro é liso, olhando no diagrama de Moody estamos em região de transição.

Batendo a curva de tubos lisos com o eixo vertical:

f = 0,014

Outros dados do enunciado:

L = 4   m

Passo 2

Substituindo os valores na expressão de perda de carga:

h p = f L d V ² 2 g

h p = 0,014 ∙ 4 0,007 ∙ 5 ² 2 ∙ 9,81

h p = 10,19   m

Passo 3

Para calcularmos a perda de pressão basta substituirmos o que conhecemos na expressão da Equação da Energia:

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

V 1 = V 2 , z 1 = z 2 , logo,

p 1 ρ g = p 2 ρ g + h p

p 1 - p 2 ρ g = h p

p 1 - p 2 = ρ g h p

p 1 - p 2 = 13550 ∙ 9,81 ∙ 10,19

p 1 - p 2 = 1354510   P a = 1354,51   k P a

Resposta

h p = 10,19   m

p 1 - p 2 = 1354,5   k P a

Exercício Resolvido #2

Querosene a 20 ° C é bombeado a   0,15   m 3 / s   por 20   k m de tubo horizontal de ferro fundido de 16   c m de diâmetro. Calcule a potência necessária de entrada em k W , se as bombas têm 85 % de rendimento.

Passo 1

Vamos com calma.

Temos mais um problema de dutos, só que neste caso devemos queremos instalar uma bomba de 85 % de rendimento. Se analisarmos a equação da energia com adição de energia da bomba:

p 1 ρ g + V 1 ² 2 g + z 1 + h b o m b a = p 2 ρ g + V 2 ² 2 g + z 2 + h p

Veremos que pelo tubo ser horizontal, sem alteração na seção transversal, e com mesma pressão em cada ponta:

p 1 = p 2

V 1 = V 2

z 1 = z 2

Portanto temos o problema reduzido a expressão:

h b o m b a = h p

Onde,

h p = f L d V ² 2 g

E,

h b o m b a = η P o t ρ g Q

O enunciado nos fornece:

Q = 0,15 m 3 s L = 20   k m d = 16   c m η = 0,85

Propriedades do querosene a 20 ℃ :

ρ = 804   k g / m ³ μ = 1,92 × 10 - 3 k g / ( m . s )

Rugosidade do tubo de ferro fundido:

ϵ = 0,26   m m

Passo 2

Vamos começar encontrando o valor do número de Reynolds para sabermos que caso de escoamento estamos:

R e d = ρ V d μ

Onde

V = Q A

V = 0,15 π 0,16 ² 4

V = 7,46   m / s

Substituindo os valores na expressão do Reynolds:

R e d = 804 × 7,46 × 0,16 1,92 × 10 - 3

R e d = 499820 > 2300

Escoamento turbulento!

Calculando a rugosidade relativa ϵ / d

ϵ d = 0,26 × 10 - 3 0,16

ϵ d = 0,001625

Para estes valores de ϵ / d e R e d , no Diagrama de Moody:

f ≈ 0,022

Agora calcularemos a perda de carga h p

h p = f L d V 2 2 g

h p = 0,022 × 20 × 10 3 0,16 × 7,46 ² 2 × 9,81

h p = 7800   m

Passo 3

Lembrando que temos h p = h b o m b a

h p = η P o t ρ g Q

P o t = h p ρ g Q η

Substituindo os valores:

P o t = 7800 × 804 × 9,81 × 0,15 0,85

P o t = 10856553   W = 10856,5   k W

Resposta

10856,5   k W

Exercício Resolvido #3

O escoamento no tubo da Figura é produzido pelo ar pressurizado no reservatório. Que pressão p 1 manométrica é necessária para fornecer uma vazão Q = 60 m 3 / h de água a 20°C?

Passo 1

Mais uma vez, vamos olhar a equação da energia e descobrir pelo enunciado qual valor de cada propriedade na entrada e na saída.

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

Queremos descobrir p 1 manométrica.

Vamos supor que o reservatório é muito grande, ou seja, não há movimentação na superfície que seja considerável, logo V 1 = 0 .

Sabemos também que:

z 1 = 10   m

z 2 = 80   m

Na figura temos que o jato na saída é livre, logo p 2 = 0 , na escala manométrica.

Se conhecemos o diâmentro do duto e a vazão, podemos calcular a velocidade:

V = Q A

V 2 = 4 Q π d ²

V 2 = 4 Q π d ²

Onde,

Q = 60 m 3 h = 0,0167 m 3 s

d = 5   c m = 0,05   m

Logo nosso V 2 é:

V 2 = 4 × 0,0167 π 0,05 ²

V 2 = 8,5   m / s

Nossa equação fica:

p 1 ρ g = V 2 ² 2 g + z 2 - z 1 + h p

Onde não conhecemos ainda h p .

Passo 2

Antes de calcularmos h p , devemos saber se o escoamento é laminar ou não.

Para isso calculamos o número de Reynolds:

R e d = ρ V d μ

Água a 20 ℃ tem as seguintes propriedades, ρ = 1000   k g / m ³ e μ = 0,001   k g / ( m . s )

R e d = 1000 × 8,5 × 0,05 0,001

R e d = 425000

Temos escoamento não-laminar.

Como o enunciado não informou nada, vamos supor que o tubo seja liso. A partir do Diagrama de Moody:

f ≈ 0,013

Substituindo na expressão de h p ,

h p = f L d V ² 2 g

h p = 0,013 60 + 80 + 30 0,05 8,5 ² 2 × 9,81

h p = 162,76   m

Passo 3

Substituindo na expressão de p 1

p 1 ρ g = V 2 ² 2 g + z 2 - z 1 + h p

p 1 = ρ g V 2 ² 2 g + z 2 - z 1 + h p

p 1 = 1000 × 9,81 8,5 ² 2 × 9,81 + 80 - 10 + 162,76

p 1 = 2319500   P a

Resposta

p 1 = 2319500   P a

Exercício Resolvido #4

Qual nível h deve ser mantido na Figura para fornecer uma vazão de 0,425   L / s pelo tubo de aço comercial de 13   m m de diâmetro?

Passo 1

Como sempre galera, devemos ver o que precisamos calcular da equação da energia:

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

Do desenho, podemos dizer que a pressão de entrada é a atmosférica, ou na escala manométrica.

p 1 = p 2 = 0

Podemos dizer também que,

z 1 = h

z 2 = 0

Supondo que o tanque de água tem uma superfície muito grande, logo:

V 1 = 0

O que nos resta de expressão:

h = V 2 ² 2 g + h p

Passo 2

Devemos calcular a velocidade de saída V 2 ,

V 2 = Q A

V 2 = 4 Q π D ²

Sabemos do enunciado que:

Q = 0,425 L s = 0,425 d m 3 s = 0,425 × 10 - 3   m ³ / s

D = 13   m m = 0,013   m

Substituindo,

V 2 = 4 0,425 × 10 - 3 π 0,013 ²

V 2 = 3,2   m / s

Passo 3

Agora para a perda de carga, calcularemos o Reynolds para termos o fator de perda de carga f :

R e d = ρ V D μ

Água a 20 ℃ : ρ = 1000   k g / m ³ e μ = 0,001   k g / ( m . s )

R e d = 1000 × 3,2 × 0,013 0,001

R e d = 41600

Temos um escoamento não laminar.

A rugosidade relativa é de,

ϵ D = 0,046 × 10 - 3 0,013 = 0,00354

O que nos leva a um fator de perda de carga no Diagrama de Moody:

f ≈ 0,028

Logo a perda de carga h p tem o seguinte valor,

h p = f L D V ² 2 g

h p = 0,028 24,4 0,013 3,2 ² 2 × 9,81

h p = 27,4   m

Passo 4

Subsituindo a perda de carga e a velocidade na expressão de h :

h = V 2 ² 2 g + h p

h = 3,2 ² 2 × 9,81 + 27,4

h = 27,9   m

Resposta

h = 27,9   m

Exercício Resolvido #5

Os dados a seguir foram obtidos para o escoamento de 20   m 3 / h de água a 20 ° C por um tubo com forte corrosão, de 5   c m de diâmetro, que está inclinado para baixo a um ângulo de 8 ° : p 1 = 420   k P a , z 1 = 12     m , p 2 = 25 0   k P a , z 2 = 3   m . Calcule (a) a rugosidade relativa do tubo e (b) a variação percentual na perda de carga se o tubo fosse liso e a vazão a mesma.

Passo 1

No enunciado ele já nos fornece o valor de algumas propriedades que aplicaremos na equação da energia:

p 1 = 420   k P a z 1 = 12   m p 2 = 250   k P a z 2 = 3   m

Podemos dizer também que V 1 = V 2 = V .

O esquema do problema é o seguinte:

Passo 2

Na equação da energia, vamos calcular a perda de carga:

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

h p = p 1 - p 2 ρ g + z 1 - z 2

A massa específica da água é ρ = 1000   k g / m ³ ,

h p = 420 - 250 × 10 3 1000 × 9,81 + 12 - 3

h p = 26,33   m

Sabemos que

h p = f L d V ² 2 g

Desta expressão conhecemos tudo menos f , L e V .

L é facilmente cálculado pela geometria do problema:

L = 12 - 3 sin ⁡ 8 °

L = 64,7   m

Já V é necessário dividir a vazão pela área transversal do tubo:

V = Q A

V = 20 ÷ 3600 π 0,05 ² 4

V = 2,83   m / s

Dividimos a vazão por 3600 pois estava em m ³ / h e não em m ³ / s .

Colocando a expressão em função de f :

f = 2 g d h p L V ²

Substituindo:

f = 2 × 9,81 × 0,05 × 26,33 64,7 × 2,83 ²

f = 0,05

Passo 3

Calcularemos agora o número de Reynolds:

R e d = ρ V d μ

Viscosidade cinemática da água μ = 0,001   k g / ( m . s )

R e d = 1000 × 2,83 × 0,05 0,001 = 141500

Para f = 0,05 , olhando no Diagrama de Moody a rugosidade relativa é aproximadamente igual a

ϵ d ≈ 0,02

Passo 4

Se o tubo fosse liso, para esse valor de Reynolds, o fator de atrito f seria próximo a 0,0165 . Então a perda de carga seria:

h p = f L d V ² 2 g

h p = 0,0165 64,7 0,05 2,83 ² 2 × 9,81

h p = 8,71   m

Tomando a razão das duas perdas de carga:

8,71 26,33 = 0,33 = 33 %

Ou seja, a perda de carga no tubo liso seria 67 % menor comparado ao caso do tubo com forte corrosão.

Resposta

a ϵ d ≈ 0,02

b   67 %

Exercício Resolvido #6

Elaboração própria

Sobre o Diagrama de Moody, analise as seguintes afirmações e afirme se são verdadeiras ou falsas.

I – O Diagrama de Moody é útil para a estimação do fator de atrito a partir do número de Reynolds e da rugosidade relativa tanto para escoamentos laminares como para escoamentos turbulentos.

II – Considerando dois escoamentos em tubos com o mesmo número de Reynolds, aquele com maior rugosidade relativa terá maior fator de atrito.

III – Em tubos lisos, o fator de atrito é zero, pois a rugosidade relativa é nula.

Passo 1

Faaaala, futuro aprovado! Tudo bem? Vamos analisar afirmação por afirmação 😊

I – O Diagrama de Moody é útil para a estimação do fator de atrito a partir do número de Reynolds e da rugosidade relativa tanto para escoamentos laminares como para escoamentos turbulentos.

Dando uma olhadinha no próprio Diagrama de Moody, vemos que no eixo x temos Reynolds, e cada curva corresponde a uma rugosidade relativa. Com isso, conseguimos encontrar no eixo y o fator de atrito.

Além disso, há curvas tanto na zona laminar quanto na turbulenta, conforme indicado na figura. Saca só:

Então, a primeira alternativa é verdadeira.

Passo 2

A segunda afirmação diz o seguinte

II – Considerando dois escoamentos em tubos com o mesmo número de Reynolds, aquele com maior rugosidade relativa terá maior fator de atrito.

Isso faz sentido, pois se apenas aumentamos a rugosidade relativa, isso significa que o atrito será maior. Se o atrito será maior, então o fator de atrito também será.

Dá para perceber isso visualmente também no diagrama. O mesmo Reynolds está representado pela reta laranja.

A rugosidade relativa azul é menor e com ela encontramos o fator de atrito próximo de 0,027.

A rugosidade relativa verde é maior e com ela, o fator de atrito é cerca de 0,035.

Logo, a afirmação II é verdadeira

Passo 3

Agora é a última afirmação, mas, dica de amiga, é muito importante!

III – Em tubos lisos, o fator de atrito é zero, pois a rugosidade relativa é nula.

Essa afirmação pode até parecer intuitiva, pois quando se fala em tubo liso, podemos acabar pensando que não há atrito! Porém, não se engane!

O fato do tubo ser liso significa que a rugosidade relativa dele é beeem baixa, próxima a zero, isso é verdade. A questão é que isso não quer dizer que o fator de atrito é zero!

“Ué?! Como assim?”

Olha só essa curva destacada no Diagrama de Moody

Isso revela que em tubos lisos, a rugosidade relativa não importa para calcular o fator de atrito. Porém, o fator de atrito não é nulo e vai depender do número de Reynolds.

Ou seja, as propriedades do fluido, a velocidade e o diâmetro do tubo vão influenciar no valor do fator de atrito, que pode ser calculado pelo Moody.

Portanto, a terceira afirmação é falsa!

Resposta

I - Verdadeira

II – Verdadeira

III - Falsa

Exercício Resolvido #7

Elaboração própria

Água a 20°C escoa por 10 m de tubo liso de 0,05 m de diâmetro a uma velocidade média de 8 m/s. Calcule a perda de carga em metros.

Passo 1

Opa! Para calcular a perda de carga h p , precisamos saber o fator de atrito f , já que:

h p = f L D V ² 2 g

Substituindo os dados do enunciado (comprimento L, diâmetro D, velocidade média V)

h p = f 10 0,05 8 ² 2   .   9,8 = 653,1 × f

Beleza, bora calcular esse fator de atrito!

Passo 2

O cálculo do fator de atrito depende se o escoamento é laminar ou turbulento. Para saber qual tipo de escoamento, o cálculo de Reynolds nos ajuda:

R e = ρ V D μ

Como o fluido é a água e substituindo os dados do enunciado também

R e = 1000 × 8 × 0,05 0,001 = 4 × 10 5

Para saber se é laminar ou turbulento, comparamos esse valor obtido com o valor de Reynolds crítico, que no caso do tubo é 2300.

4 × 10 5 > 2300

Como Reynolds é maior que 2300, então o escoamento é turbulento!

Logo, o fator de atrito deve ser calculado pela rugosidade relativa e Reynolds aplicados no Diagrama de Moody.

Passo 3

Já conhecemos o Reynolds, mas não sabemos ainda a rugosidade relativa. Repara que o enunciado não informa o material do tubo, mas diz que ele é liso. Essa informação é suficiente para já utilizar o Diagrama de Reynolds

Utilizando a curva do tubo liso e R e =   4 × 10 5 no Diagrama de Moody,

Encontramos que o fator de atrito é f = 0,013! :D

Passo 4

Voltando ao cálculo da perda de carga

h p = 653,1 × f

Substituindo

h p = 653,1 × 0,013

h p = 8,5   m

Logo, a perda de carga é 8,5 m. Yay!

Resposta

h p = 8,5   m

Exercício Resolvido #8

Elaboração própria

O escoamento de água a 20°C ocorre em regime de turbulência completa em um tubo de 0,02 m de diâmetro de aço inoxidável novo. Calcule o fator de atrito.

Passo 1

Oi! :D O cálculo do fator de atrito depende do escoamento ser laminar ou turbulento.

Normalmente, calculamos o número de Reynolds desse escoamento e verificamos se é menor ou maior que 2300 para ver se é laminar ou turbulento, respectivamente.

Poréééém, dessa vez o enunciado facilitou nossa vida e já disse que o regime é de turbulência completa. Vamos dar uma olhada no diagrama

Como vimos na teoria, no regime de turbulência completa, o número de Reynolds já não influencia mais no cálculo do fator de atrito, que por sua vez vai depender somente da rugosidade relativa.

Então vamos a ela!

Passo 2

A rugosidade relativa é a razão entre a rugosidade e o diâmetro do tubo ⇒ e D

E a rugosidade depende do material, que é aço inoxidável novo. Pela tabela de rugosidade

A rugosidade do aço inoxidável novo é 0,002 mm

e = 0,002   m m = 2 × 10 - 6   m

A rugosidade relativa é então:

e D = 2 × 10 - 6   m 0,021   m

e D = 0,000095 ≈ 0,0001

Aplicando esse valor no Diagrama de Moody

Encontramos o fator de atrito igual a 0,012, conforme podemos visualizar melhor no zoom

Partiu próximo exercício? :D

Resposta

f = 0,012

Exercícios de Livros Relacionados

Petróleo está escoando de um grande tanque em uma colina para um petroleiro no cais. O compartimento de carga no navio está quase cheio e um operador inicia o processo de interrupção do escoamento. Um
Um tanque contendo 30 m3 de querosene deve ser esvaziado por gravidade usando uma mangueira de drenagem de diâmetro 15 mm, rugosidade 0,2 mm e comprimento 1 m. O topo do tanque está aberto para a atmo
Água a temperatura ambiente escoa à mesma vazão volumétrica, Q = 9,4 × 10 - 4m 3 / s , por dois tubos, um de seção circular e outro de seção anular. A área da seção transversal A dos dois tubos é idên
John Laufes (NACA Tech. Rep. 1174, 1954) forneceu dados de velocidade para escoamento de ar a 20°C em um tubo liso de 24,7 cm de diâmetro com R e ≈ 5 E 5 :A velocidade na linha de centro u L C era 30,
O sifão mostrado é fabricado de tubo de alumínio trefilado de 50 mm de diâmetro interno. O líquido é água a 15°C. Calcule a vazão volumétrica através do sifão. Estime a pressão mínima no interior do t