Perdas localizadas e Dutos não-circulares
Teoria
Dutos não-circulares
Fala chefe! Tudo certo?
Bom, provavelmente você deve ter visto em algum lugar essas tubulações de ar:
Ou essas daqui:
Elas tem algo em comum que é o fato delas não serem circulares, isso muda um pouco nossa abordagem sobre escoamentos em dutos, porque o escoamento não é aquele que a gente tava vendo, com aqueles fatores de atrito e tudo mais.
Mas não muda muita coisa, fica tranquilo todo seu esforço terá valido a pena aqui também!
Uns caras pensando em realizar esses escoamentos nesses dutos não convencionais fizeram algumas relações algébricas e tudo mais e chegaram no conceito de Diâmetro Hidráulico :
Esse diâmetro é meio que um substituto pro diâmetro de círculos mesmo. Então todas as outras fórmulas ainda valem! Yey...
Vamos dar nomes aos bois:
Isso de “perímetro molhado” é onde o fluido toca o duto. Normalmente o perímetro da seção.
Por exemplo, na figura a seguir, o fluido encosta em todo o perímetro da tubulação retangular de 2 metros de altura e 3 metros de largura).
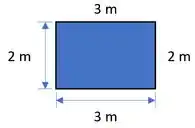
Logo, o perímetro molhado é Esse valor coincide com o perímetro da seção pois o fluido está molhando toda a seção.
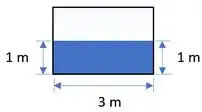
Se o fluido estivesse na metade da altura do mesmo duto, como mostrado na figura a seguir, o perímetro molhado seria outro:
Então é só substituirmos nas nossas expressões esse :
Assim tudo muito bonito e tal, mas é bom entender que isso tudo são aproximações pra gente poder continuar usando nossas fórmulas de antes. Ou seja, os nossos resultados apresentam um erro.
No escoamento turbulento esse erro é bem pequeno, mas no caso laminar a coisa fica um pouco mais complicada. Vou descrever rapidinho como ficam as expressões de no caso laminar:
-Seção retangular e triangular:
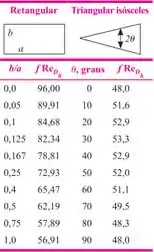
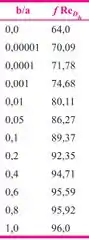
-Seção em anel ( é o raio maior e o raio menor):
Ou usa essa tabelinha:
Perdas Localizadas
Seguindo nossos estudos, vamos dar uma olhada em um negócio chamado perda localizada.
O que significa esse troço? Significa que podem existir coisas nas nossas tubulações que dão mais dificuldade do fluido se movimentar. Mas por quê alguém faria isso?
Porque a gente precisa fechar ou diminuir o escoamento, a gente precisa controlar o escoamento, por isso usamos válvulas. Só por curiosidade, vou jogar um exemplo de como é uma válvula aqui:
Mas também temos perdas por causa de curvas ou cotovelos na nossa tubulação. É a mesma coisa quando estamos no trânsito, chega na hora da curva ou a gente freia o carro ou a gente sai voando da pista. Como o fluido ta preso pelos dutos, ele não tem a escolha de sair voando. Mas imagina que louco um fluido derrapando...
Contrações ou expansões também fazem a gente perder energia, se olhar essa figurinha aqui em baixo isso fica claro:
TODO MUNDO FREIA QUANDO JUNTA AS PISTAS!
Trânsito e sua extrema familiaridade com escoamentos fluidos...
Sem mais delongas vamos ver como calcular essas perdas.
Lembra do das perdas de carga globais? Agora a gente vai ter um carinha chamado perda de carga localizada.
Normalmente essas perdas são calculadas experimentalmente, então em breve veremos várias tabelas de um valor chamado coeficiente de perda localizada . Ele se relaciona com assim:
Lembrando que a gente pode ter um monte de perdas localizadas, mas é só fazer o somatório delas que ta tudo tranquilo.
Se você quiser, podemos reescrever nossa equação da energia, com um formato mais geral:
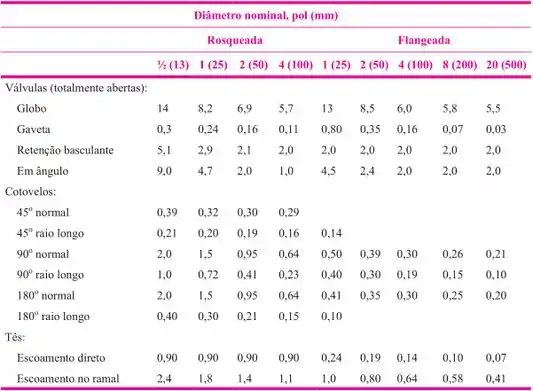
Aqui em baixo vou colocar uma tabelinha de valores de de válvulas, cotovelos, em função do diâmetro da tubulação, só pra gente ter uma ideia de como funciona. Existem vários tipos de tabelas e gráficos que descrevem perdas locais. Conforme aparecerem nos exercícios a gente aplica elas.
Então show? Bora praticar?
Perdas Localizadas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Em um trecho de 30 m de comprimento e 50 mm de diâmetro de uma tubulação de ferro galvanizado, água escoa e passa por uma válvula gaveta totalmente aberta, 2 cotovelos de 90° normal e um cotovelo de 45° normal também. Considerando que os acidentes são rosqueados e vazão é de , calcule a perda de carga localizada.
Passo 1
Bom dia, boa tarde, boa noite ou boa madrugada! xD Vamos começar a resolver os exercícios de Perdas Localizadas :D
Vimos na teoria que a perda localizada é o somatório de todas as perdas causadas por acidentes (obstáculos) no trecho analisado. Dá uma olhada:
Sendo o coeficiente de perda localizada de cada acidente e a velocidade do fluido que passa pelo obstáculo.
No nosso caso, todos os acidentes estão acontecendo numa tubulação de diâmetro 50 mm. A partir daí conseguimos calcular a velocidade e ela será a mesma para todo mundo. Podemos coloca-la para fora o somatório
Precisamos de duas coisas para calcular a perda de carga então: calcular a velocidade e descobrir os coeficientes dos acidentes! Primeiro vamos calcular a velocidade pela vazão volumétrica
A área é a área de um tubo circular de diâmetro 50 mm, ou seja, 0,05 metros. Sempre bom usar o Sistema Internacional (SI)! Aliás, a vazão também precisa ser convertida para o SI.
Com isso achamos a velocidade na tubulação
Passo 2
Agora vamos encontrar os coeficientes de perda localizada. Os acidentes são:
- 1 válvula gaveta totalmente aberta
- 2 cotovelos de 90° normal
- 1 cotovelo de 45° normal
Lembrando que são rosqueados e o diâmetro é de 50 mm, hein! Vamos ver isso na tabela
Assim, pela tabela encontramos que
Calculando a perda localizada
Detalhe importante! Multiplicamos o K do cotovelo de 90° por 2, pois temos esse mesmo acidente 2 vezes. Os outros não foram multiplicados porque só tem 1 de cada. Fechado?
Vamos as contas. Substituindo
Perda localizada calculada! =D
Resposta
Exercício Resolvido #2
Elaboração própria
Uma tubulação de aço comercial tem 5 m de comprimento e 13 mm de diâmetro. Água escoa a 0,2 L/s passando por uma válvula globo rosqueada totalmente aberta e um cotovelo de 90° normal rosqueado. Calcule (a) a perda de carga global, (b) a perda de carga localizada e (c) compare os valores e analise qual tipo de perda é mais significativo nesse trecho.
Passo 1
Olá! Nesse exercício vamos relacionar os dois tipos de perda que aprendemos. Daqui para frente vamos sempre estar atentos a eles.
Sobre a perda de carga global , aprendemos que ela depende do comprimento da tubulação, do diâmetro, da velocidade do tubo e do fator de atrito
Vamos primeiro calcular essa velocidade, pois vamos usar esse valor ao longo de todo o exercício, já que o diâmetro da tubulação permanece o mesmo.
Sendo um tubo circular, a área é:
Substituindo o que conhecemos do enunciado e passando a vazão para o m³/s:
Assim encontramos a velocidade:
Passo 2
Para o cálculo da perda global, falta conhecer o fator de atrito. Esse cálculo depende se o escoamento é laminar ou turbulento. Então vamos analisar Reynolds.
Considerando que o fluido é a água, substituímos
Como Reynolds é maior que 2300, então o escoamento é turbulento. Logo, o fator de atrito depende de Reynolds e da rugosidade relativa .
Falando nela... Sendo o tubo de aço comercial, pela tabela de rugosidade, .
Com e , usamos o Diagrama de Moody
O fator de atrito é aproximadamente 0,032 como indicado no zoom.
A reta laranja não está traçada exatamente na curva de 0,004 de rugosidade relativa, pois o valor mais preciso é 0,0035. Por isso, foi marcada um pouco abaixo. Beleza?
Agora vamos substituir os valores para encontrar a perda de carga:
Passo 3
Até aqui, encontramos a perda de carga global. Vamos analisar a letra b, que pede a perda localizada:
é o coeficiente de perda localizada de cada acidente e a velocidade do fluido que passa pelo obstáculo.
Como todos os acidentes estão num trecho de mesmo diâmetro, então a velocidade é a mesma que já calculamos.
Ok! Para encontrar os coeficientes de perda localizada, vamos fazer uma lista dos obstáculos que o fluido passa:
- 1 válvula globo totalmente aberta
- 1 cotovelo de 90° normal
Vamos encontrar na tabela. O diâmetro é 13 mm e são acidentes rosqueados
Assim, pela tabela encontramos que:
Calculando a perda localizada:
Substituindo:
E assim encontramos a perda localizada!
Passo 4
Finalmente, vamos a letra c, fazer uma comparação
O escoamento nas condições apresentadas nesse exercício tem perda global (causada pelo escoamento do fluido ao longo da tubulação) de 1,43 m e perdas localizadas (causadas pelos acidentes) de 1,86 m.
Então, nesse caso, a perda localizada é maior que a perda global, a perda localizada é mais significativa. Beleza, ok... Mas o que isso quer dizer?
Por exemplo, se quiséssemos atuar para diminuir as perdas desse trecho, seria interessante atuar nos obstáculos e trocá-los por outros que tenham um coeficiente de perda localizada menor! Isso teria mais impacto do que trocar o material do tubo, por exemplo.
É muito importante lembrar que se a situação fosse outra (outro material da tubulação, outro comprimento, outros acidentes), a perda de carga global poderia ser mais significativa. Para fazer essa afirmação de quem é mais significativa, precisamos analisar cada escoamento, ok? o/
Resposta
Exercício Resolvido #3
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 513, ex. 8.169
(Adaptada) Um grande reservatório fornece água para a comunidade. Uma parte do sistema de abastecimento de água é mostrada. A água é bombeada de um reservatório para um grande tanque de armazenagem antes de ser enviada para a instalação de tratamento de água. O sistema é projetado para fornecer 1310 L/s de água a 20°C. De B para C, o sistema consiste em uma entrada da borda-viva, 760 m de tubo, três válvulas gaveta, quatro cotovelos de 45° e dois cotovelos de 90°. Todo o tubo é de ferro fundido de 508 mm de diâmetro e fator de atrito 0,017. Calcule a perda localizada no trecho BC.
Passo 1
Para calcular a perda localizada, uma das opções é calcular assim:
é o coeficiente de perda localizada de cada acidente e a velocidade do fluido que passa pelo obstáculo.
Porém, repara que nesse exercício, o diâmetro é de 508 mm e que não foi dito se é flangeado ou rosqueado. Nesse caso, o uso da tabela que temos dos coeficientes K só ajuda para calcular a parte da entrada, cujo K conhecemos e é 1. E para os outros acidentes?
Relaxa que esse caso tem solução! Temos informação sobre o fator de atrito e a tabela de comprimentos equivalentes para cada acidente dito no enunciado. Isso vai nos ajudar muito!
E com isso, vamos usar a seguinte fórmula:
Como a tubulação tem o mesmo diâmetro no trecho BC e mesmo material, f e V são os mesmos para todos os acidentes:
Precisamos conhecer a velocidade V e os de cada obstáculo. Começando pela velocidade:
Como o duto é circular, a área é:
Substituindo os valores e convertendo a vazão para o m³/s:
Logo, a velocidade é
Passo 2
Fazendo uma lista dos acidentes que ocorrem no trecho BC:
- 1 entrada da borda-viva
- 3 válvulas gaveta
- 4 cotovelos de 45°
- 2 cotovelos de 90°
Pela tabela a seguir, encontramos os valores de para cada acidente.
Lembrando que para a entrada sabemos que o K é 1. Substituindo na equação da perda localizada
Show! Encontramos a perda de carga localizada.
Resposta
Exercício Resolvido #4
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
A Figura mostra um ensaio de perdas para um filtro espesso. A vazão no tubo é de e a pressão a montante é de . O fluido é o ar a . Usando a leitura do manômetro de coluna de água, estime o coeficiente de perda do filtro.
Passo 1
Calma galera, sei que parece um pouco diferente, mas é um exercício parecido com o que estamos fazendo, ou seja:
Bora montar a equação da energia! (só não grita de emoção, pode atrapalhar os coleguinhas do lado)
Vamos então cancelar os termos que não variam da entrada para a saída:
-Não varia a altura do duto:
-Não varia a vazão nem a área, logo não varia a velocidade:
-Vamos supor que as perdas globais são desprezíveis.
Nossa equação fica com a seguinta cara então:
Passo 2
Agora as coisas mudam um pouquinho, pois temos essa perda local do filtro.
Vamos colocar esse valora na equação:
Arrumando as coisas:
Beleza então precisamos calcular os termos e .
Lembra daquela expressão de gases perfeitos ?
Podemos aproximar o ar como um gás perfeito para calcular sua massa específica, ou consultamos alguma tabela que tenha os valores para e .
Logo
A velocidade podemos calcular pela vazão e pela área
Agora podemos olhar o manômetro para calcular a pressão na saída .
Se lembrarmos lá do início da Hidrostática, podemos fazer um balanço de pressões:
Se reorganizarmos isso veremos que o termo aparece:
Logo
Substituindo tudo na expressão de :
Resposta
Exercício Resolvido #5
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Na Figura encontram-se de tubo de , de tubo de e de tubo de , todos de ferro fundido. Há também 3 cotovelos de e uma válvula globo aberta, todos flangeados. Se a elevação de saída é zero, qual é a potência em extraída pela turbina quando a vazão é de de água a ?
Formulário:
-Contração Brusca:
-Expansão Brusca:
Passo 1
Nesta questão devemos mais uma vez montar a equação da energia:
Repare que temos dois somatórios:
-Das perdas globais
-Das perdas locais
-Além da energia que a turbina precisa
Nos próximos passos listaremos cada uma das perdas que vamos calcular.
As condições de entrada são:
Na saída:
Logo a equação fica com a seguinte cara:
Rearranjando em função da turbina:
Passo 2
Como já conhecemos e , vamos listar e calcular as perdas globais, existem três pois temos três variações de diâmetro na tubulação:
é do tubo de com diâmetro ;
é do tubo de com diâmetro ;
é do tubo de com diâmetro .
Comecemos pela primeira perda :
Calcularemos a velocidade e então o número de Reynolds, sendo e :
Dado que a rugosidade do tubo é
Logo, pelo Diagrama de Moody,
Substituindo na expressão da perda de carga:
Fazendo o mesmo para as outras duas perdas de carga:
Para a terceira:
Somando todas as três perdas:
Passo 3
Agora vamos listas as perdas locais:
- Na entrada da tubulação, contração brusca;
- 3 cotovelos de normal;
- 1 válvula globo aberta;
- Na saída, expansão brusca.
Na contração:
Se :
Nos cotovelos, olhamos valores tabelados:
Na válvula, também pegamos valores tabelados:
Na expansão brusca:
Logo nosso somatório fica:
Passo 4
Lembrando da expressão que deduzimos no primeiro passo, iremos substituir as variáveis que não conhecíamos:
Logo a potência da turbina em é igual a :
Resposta
Exercício Resolvido #6
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Uma grande sala usa um ventilador para succionar o ar atmosférico a por um duto de aço comercial de por por de comprimento, como na Figura P6.92. Calcule a pressão na sala, se a vazão for . Despreze as perdas localizadas.
Passo 1
Neste exercício devemos estamos considerando um duto não circular! É um duto de seção quadrada.
Antes de calcularmos o diâmetro hidráulico, vamos como sempre olhar a equação da energia. Vamos considerar que nosso volume de controle começa no início do duto e termina na entrada da sala.
Tanto a velocidade, quanto a altura não muda de um ponto a outro do duto, logo a equação fica com a seguinte cara:
Passo 2
Vamos calcular o número de Reynolds para sabermos o tipo de regime em que estamos:
Calculamos o diâmetro hidráulico :
Se a velocidade é
As propriedades do ar são e
Se a velocidade é
Logo
Regime turbulento, podemos usar o Diagrama de Moody como aproximação.
Passo 3
Sabemos que o material é aço comercial, logo:
No Diagrama de Moody:
Passo 4
Substituindo na expressão inicial da equação da energia:
Como queremos :
Neste caso vamos usar a escala absoluta de pressão:
Substituindo todos valores, temos a expressão:
Resposta
Exercício Resolvido #7
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 444, ex. P 6.91
(Adaptada) Trocadores de calor consistem frequentemente em muitas passagens triangulares. Uma passagem é mostrada na figura, com e seção transversal em formato de um triângulo isósceles de comprimento lateral e ângulo . Se a velocidade média é e o fluido é óleo SAE 10 a 20°C, calcule a perda de carga global.
Dados: ,
Passo 1
Esse é um exercício de duto não-circular. Por isso, vamos precisar do diâmetro hidráulico para fazer os cálculos de Reynolds. Com o Reynolds descobrimos se o escoamento é laminar ou turbulento. Então vamos lá,
A área da seção do duto é a área do triângulo isósceles. Sabemos o lado a e o ângulo entre os lados iguais, então é conveniente usar essa fórmula de área do triângulo
No triângulo isósceles, a = b
Como a = 2 cm = 0,02 m e β = 80°
Show! Para calcular o perímetro molhado vamos considerar que o fluido escoa ao longo de todo o perímetro. Logo, o perímetro molhado será o próprio perímetro.
Podemos levar isso em consideração, pois o enunciado não informa se o fluido estaria ocupando apenas uma parte do duto. Beleza?
Conhecemos dois lados do triângulo, mas falta conhecer o terceiro. Para isso, vamos usar a lei dos cossenos
No triângulo da figura
Substituindo
Calculando o perímetro molhado
Voltando ao Diâmetro hidráulico
Passo 2
Opa! Com esse diâmetro hidráulico, vamos calcular Reynolds! :DD
Substituindo
Como Re é menor que 2300, o escoamento é laminar. Por isso, vamos usar a tabela que relaciona o fator de atrito e Reynolds no escoamento laminar a depender da geometria (nosso caso é triangular)
Por que selecionar o ? Pois nessa tabela, o ângulo entre os lados iguais é . Então
Pela tabela vemos que:
E assim podemos calcular a perda de carga global 😊
Resposta
Exercício Resolvido #8
Frank M. White, Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH, 2011.
Um duto de seção anular de folga muito pequena provoca uma queda de pressão muito grande e é útil para uma medição precisa da viscosidade. Se um duto de seção anular liso de de comprimento, com e , transporta uma vazão de óleo a , qual é a viscosidade do óleo se a queda de pressão é ?
Passo 1
Montaremos nossa equação da energia deste sistema:
Vamos supor que não há variação na altura logo ;
Pelo enunciado não parece que há uma variação na área a seção, e como é constante:
Pelo enunciado sabemos também que .
Portando nossa equação fica:
Passo 2
Fórmula da perda de carga para seções não circulares:
Calcularemos primeiro o diâmetro hidráulico :
A área é igual a,
O perímetro molhado :
Logo :
Agora calcularemos a velocidade a partir da área e da vazão :
Vamos supor escoamento laminar, logo,
Ao invés de utilizarmos aquela expressão longa de , vamos utilizar aquela tabelinha que vimos na teoria:
Logo , ou seja, .
Passo 3
Substituiremos os tudo na equação da energia:
Sabemos que :
Substituindo :
Rearranjando em função de :
Logo,