Medidores de vazão: orifício, bocal e venturi
Teoria
Medição Direta de Vazão
Para medir o comprimento de um tubo, usamos uma trena! Para medir tempo, usamos o cronômetro. Para medir a diferença de pressão entre dois pontos em uma tubulação, usamos o manômetro.
E para medir vazão? Nos exercícios sempre dizemos que a vazão é um certo valor, maaaas, como medir? Como garantir que por ali está passando 8l/min de água?
Tenho uma solução! A gente pode usar um tanque e num intervalo de tempo fixo, vamos medir o quanto de volume o fluido ocupou nesse tanque! Como a vazão volumétrica representa o quanto de volume de um fluido está escoando no tempo, então a gente encontraria Q
Esse é o método direto de medição de vazão. Dá para gente fazer na nossa casa, para descobrir por exemplo a vazão do chuveiro ou de uma torneira.
Mas, em escoamentos internos, ou seja, dentro de dutos, fica um pouco complicado usar esse método. Afinal, como calcular o volume que passa num intervalo de tempo dentro de uma tubulação?
Medidores de Vazão de Restrição
Existem outras formas de medição de vazão além da direta e vamos aprender 3 delas hoje! :D Pela placa de orifício, bocal e medidor de Venturi. Vamo que vamooo
Essas três formas tem o mesmo princípio: a restrição! É o seguinte, o fluido tá lá na tubulação, escoando de boas e de repente encontra um obstáculo... um empecilho, seu caminho é diminuído, restrito. Essa figura ilustra um exemplo de restrição:
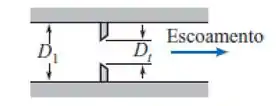
Com essa mudança no diâmetro, concorda que vai acontecer uma mudança na pressão também? Isso tá escrito nas estrelas, quer dizer, na equação da energia, nossa amiga para sempre
Repara que escrevi a equação de Bernoulli, ou seja, na nossa medição de vazão, por enquanto, não tá rolando perda de carga! Afinal, a parte do tubo que estamos analisando é curta! Então desprezamos a perda de carga . Aquela que é dada pela fórmula
Os termos z se cancelam por que estamos na horizontal. E aí reorganizando, temos o seguinte:
Aí, pela conservação da massa, a gente sabe que:
Como é o mesmo fluido:
Combinando essas duas equações (conservação da massa e da energia) e isolando a vazão mássica , a gente pode escrever que:
Essa equação diz algo interessante para quem quer medir vazão! A vazão é proporcional ao quadrado da diferença de pressão. Olha só
E o que isso tem de bom? Vazão em tubos ainda não sabemos medir, mas diferença de pressão sabemos sim :D Os medidores de vazão por restrição vão se fazer valer disso
Mas isso ainda não é tudo, tem algo muito importante agora. Até aqui, não consideramos nenhuma perda no processo, então essa vazão aí é uma vazão teórica.
Só que, ao melhor estilo Cazuza, a realidade chega e nos diz: “Tuas ideias não correspondem aos fatos!”. Como assim? =O
Calma! 😊 Traduzindo pra MecFlu, a realidade diz: “Não esquece que sou rebelde e vai rolar perdas nesse processo, tá?”
Vazão mássica real
Nessa restrição de diâmetro, ocorre perda de energia, mas não é a tal perda de carga porque essa parte do tubo é curta. Para corrigir o valor da vazão mássica, vamos multiplicar a vazão mássica teórica por um coeficiente de descarga C:
É com essa vazão que vamos trabalhar aqui! E para não ter que escrever essa razão entre áreas toda hora, vamos usar o , que é a razão entre os diâmetros de saída (t) e de entrada (1)
Como estamos considerando dutos circulares, , ou seja
Substituindo na equação da vazão mássica real:
Esse termo nós vamos chamar de fator de velocidade de aproximação
Como temos dois fatores nessa equação (C e ), podemos juntar eles num só para deixar a equação ainda mais simples. O coeficiente de vazão K é
E equação fica assim 😊
Como queremos calcular a vazão, estamos quase lá. Diferença de pressão é possível medir com o manômetro e a massa específica, sabemos do fluido. Só falta saber...
...como encontrar os coeficientes de descarga (C) e o de vazão (K)?
Os coeficientes C e K vão depender do medidor de vazão que está sendo utilizado! Em geral, nos exercícios vamos utilizar uma equação ou um gráfico, que relacionam esses coeficientes ao número de Reynolds logo antes da medição.
Essas equações são válidas para uma certa faixa de Reynolds. Se quisermos saber além dela, teremos que fazer experimentos. Mas relaxa, os exercícios costumam dar a equação/gráfico que precisamos :D
As equações são desse tipo aqui:
Essas são as equações de correlação, onde e são os coeficientes calculados para Reynolds infinitos. Todos esses valores () serão dados para cada medidor. Ou então um gráfico será dado. De qualquer forma, sabendo o Reynolds, saberemos C ou K.
Então vamos ver três tipos de medidor de restrição para escoamento interno: placa de orifício, bocal e Venturi.
Placa de orifício
Já que precisamos diminuir o diâmetro para medir a vazão, um dos meios físicos mais simples de fazer isso é instalar 2 placas que impeçam a passagem do fluido por todo o diâmetro. Essa é a ideia do medidor placa de orifício, como mostra a figura
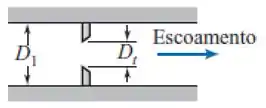
Como a instalação é simples, o custo inicial é barato. Porém, há duas principais desvantagens. Se o fluido tiver material em suspensão, ele tende a se acumular na placa ao longo do tempo. Além disso, a expansão após a placa não é controlada e com isso, a perda de carga é alta, o que não desejamos!
Dependendo da relação custo/benefício, a placa de orifício pode ser utilizada no nosso projeto. E para isso, precisaremos saber sua equação de correlação. Vamos considerar esse medidor de orifício concêntrico com tomadas de canto
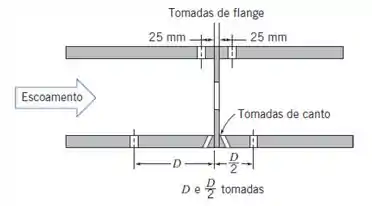
A equação de correlação dele é
Ela é válida para β entre 0,2 e 0,75 e entre e
Também podemos usar o gráfico que relaciona K com Reynolds para medidores de orifício concêntricos com tomadas de canto. Cada curva corresponde a um valor de β
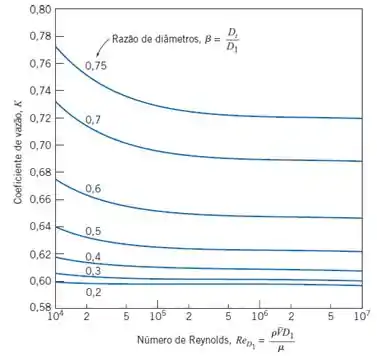
Bocal medidor
Para diminuir o diâmetro do escoamento interno, podemos também utilizar um bocal, que pode ser representado assim:
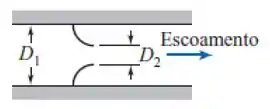
Instalar um bocal é mais complicado do que instalar uma placa de orifício, já que envolve a redução gradual do diâmetro. Por isso seu custo inicial é maior que o do orifício. ☹
Por outro lado, o bocal tem a vantagem de gerar uma perda de carga não tão alta quanto a da placa, porque a passagem do fluido por ele não é tão abrupta. 😊
Todos os tipos de medidores têm vantagens e desvantagens. Uns quanto ao custo e outros quanto a perda de carga. O bocal tem custo e perda de carga intermediários (em relação ao medidor de orifício e o Venturi)
Sua equação de correlação é
Ela é válida para β entre 0,25 e 0,75 e entre e
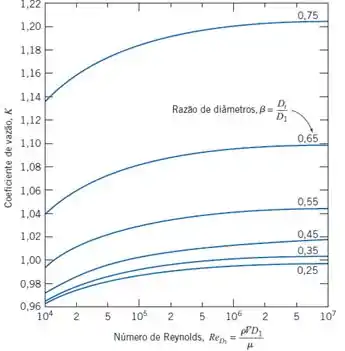
O gráfico de K e Re para bocais de raio largo é
Medidor de Venturi
O medidor de Venturi é óóótimo porque a perda de carga nele é baixa! Como ele garante isso?
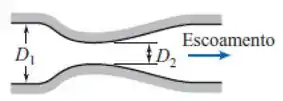
A saída (parte a jusante) dele é suave, e o diâmetro vai aumentando aos poucos de novo. Isso é o que faz o difusor cônico a jusante. Assim, ele consegue recuperar a pressão e perde menos carga.
Maaaaas, se um por um lado a perda de carga é baixa como gostaríamos, temos que pagar um preço por isso. E já aviso, preço caro. Uma pena! Além de pesado. Em um projeto, temos que ver se vale a pena essa relação custo/perda de carga.
Para valores de Reynolds altos, podemos usar C = 0,99 para os medidores Venturi. Se não pudermos assumir isso, o exercício traz a correlação a ser utilizada 😉
E esses são os medidores de vazão de restrição! Vamos medir essa vazão! o/ Preparamos uma lista de exercícios para você! :D
Vazão mássica real
...como encontrar os coeficientes de descarga (C) e o de vazão (K)?
Placa de orifício
Bocal medidor
Medidor de Venturi
Exercícios Resolvidos
Exercício Resolvido #1
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 516, ex. 8.193
Água a 65°C escoa através de um orifício com diâmetro de 75 mm instalado em um tubo de 150 mm de diâmetro interno. A vazão é 20 L/s. Determine a diferença de pressão entre as tomadas de canto.
Passo 1
Faaaaala! Começamos aqui nossos exercícios de medidores de vazão e este aqui quer saber a diferença de pressão . Show de bola!
Logo no início, o enunciado fala que nosso medidor de vazão é do tipo orifício. Ou seja, é nesse estilo:
Além disso, foi o diâmetro do orifício () e o diâmetro do tubo (). Assim, conseguimos encontrar a razão β
Também foi dada a vazão, que é 20 L/s. Repara que essa é a vazão volumétrica Q, pelas unidades de volume por tempo. No Sistema Internacional:
Passo 2
Para encontrar a diferença de pressão em um medidor de vazão de restrição (que é o caso, pois é de orifício), usamos a seguinte fórmula
Mais especificamente
Nesse exercício foi dada a vazão volumétrica e não a mássica! Por isso, vamos usar
Substituindo os dados do enunciado
Além disso,
Logo, para calcular a diferença de pressão, só falta conhecer o coeficiente de vazão K
Passo 3
Para calcular K, precisamos calcular o número de Reynolds antes da medição, isto é,
Não foi dada a velocidade, mas foi dada a vazão volumétrica, então vamos usar sua definição
Assim, podemos calcular o número de Reynolds :D
Opa! Estamos quase lá! Na teoria, vimos que podemos usar esse gráfico aqui para calcular K em placas de orifício
Conhecemos Reynolds, e ele é aproximadamente e sabemos que . Utilizando esses pontos no gráficos, temos que...
...K é aproximadamente 0,624
Substituindo esse valor na fórmula da vazão mássica real que desenvolvemos até agora
Elevando os dois lados da equação ao quadrado
Logo, a diferença de pressão é de
Resposta
Exercício Resolvido #2
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 451, ex. P 6.141
Gasolina a 20°C escoa a em um tubo de 10 cm de diâmetro. Desejamos medir a vazão com uma placa de orifício e um transdutor de pressão diferencial que fornece as melhores leituras a cerca de 55 kPa. Qual é a razão β adequada para o orifício?
Dados: e
Passo 1
Nesse exercício, nosso medidor de vazão é uma placa de orifício. Olha ela aí
Só que ao invés de querer descobrir a vazão ou a diferença de pressão, o enunciado pede a razão β, ou seja
Vamos organizar o que o enunciado deu, passando tudo para o Sistema Internacional. Primeiramente, foi dada a vazão volumétrica Q
O diâmetro do tubo é de 10 cm, ou seja
Além disso, quando o enunciado diz que o “transdutor de pressão diferencial que fornece as melhores leituras a cerca de 55 kPa”, podemos escrever que
Além disso, como conhecemos o fluido, que é a gasolina e sabemos a sua massa específica a 20°C, então podemos calcular a vazão mássica
Passo 2
Na teoria, vimos que a expressão da vazão mássica real é
ou
Como queremos encontrar a razão β, vamos usar a primeira! 😊 Nela, já conhecemos a vazão mássica, a massa específica e a diferença de pressão. Ainda não conhecemos sobre a geometria e sobre o C, o coeficiente de descarga.
Para achar C, precisamos do número de Reynolds antes da medição da vazão.
Por sua vez, a velocidade é vazão volumétrica sobre área, então ficamos com as contas assim:
Simplificando
Substituindo os valores
A partir desse Reynolds, podemos consultar o gráfico C x Re
Repara que no número de Reynolds encontrado, todas as curvas associadas à razão β, fornecem resultado de coeficiente de descarga C próximo a 0,61
Assim, vamos utilizar esse valor na fórmula da vazão mássica para encontrar o β
Passo 3
Reescrevendo a equação da vazão mássica
Além disso, essa pode ser escrita em função de β, já que
Substituindo na equação da vazão mássica
Substituindo os valores dados no enunciado e os encontrados até aqui
Fazendo as contas
Elevando ao quadrado os dois lados da equação
A razão entre os diâmetros da garganta e o inicial é 0,66.
Resposta
Exercício Resolvido #3
Fox, McDonald, Pritchard. Introdução à Mecânica dos Fluidos, 8ª ed. Gen LTD Editora, 2014, pp. 516, ex. 8.192
Um orifício de borda viva, com tomadas de canto, e um manômetro de coluna de água são usados para medir vazão de ar comprimido. Os seguintes dados são disponíveis:
Diâmetro interno da linha de ar: 150 mm
Diâmetro da placa de orifício: 100 mm
Pressão a montante: 600 kPa
Temperatura do ar 25°C
Deflexão do manômetro 750 mmH2O
Calcule a vazão em volume na linha, expressa em metros cúbicos por hora.
Passo 1
Temos um exercício que pede a vazão (eba! Vamos medir vazão, o objetivo desse tópico! :D) e o instrumento utilizado é placa de orifício.
Organizando os dados, temos que:
Diâmetro interno da linha de é o diâmetro antes da medição, logo:
Diâmetro da placa de orifício é Dt
A partir desses dois dados, já podemos calcular β
A temperatura do ar é 25°C, ou seja, 298 K
E o que nos interessa a respeito da pressão aqui é o . Esse é o termo que entra no cálculo da vazão. O enunciado informa que , mas não informa ☹
Mas relaxa! Quando ele diz que a “deflexão do manômetro 750 mmH2O”, ele está falando justamente do ! Só que temos que passar para o sistema internacional, para calcular certinho, com coerência nas unidades
Como a diferença de pressão é bem pequenininha (a pressão atmosférica é da ordem de , por exemplo), podemos considerar esse escoamento de ar incompressível. Mas só por causa disso, ok? 😉
Com isso, conseguimos calcular sua massa específica ρ. Usando pv=nRT
E multiplicando pela massa molar MM do ar, que é 0,02884 kg/mol a 25°C
Substituindo os valores de pressão e Temperatura antes da medição (a montante)
Passo 2
Além dessses dados, o que mais precisamos para calcular a vazão?
Primeiro, vamos reescrever essa área da garganta (At) aí. Atualizando a equação da vazão:
Conhecemos todos os valores, menos o K. Para saber quem ele é, precisamos usar o gráfico de K em relação a Reynolds para a placa de orifício informada.
Quem é Reynolds? Nosso querido e amado
Não temos a velocidade em 1, mas podemos escrever como vazão volumétrica sobre área
O que deixa nosso Reynolds assim
Reynolds, que é quem precisamos saber para achar K e consequentemente encontrar a vazão depende da vazão volumétrica. E aí? Como faz agora?
Aqui mora uma sacada muito boa! Vamos ver o gráfico de K versus Re. Repara que para valores de Reynolds maiores que , para cada curva, o K é praticamente o mesmo!
Cada curva está associada a um β. Nosso β é 0,66. Como não temos essa curva, vamos usar um valor entre as curvas de β =0,6 e 0,7. Assimi, encontramos K = 0,675.
Tá, mas como vamos conferir se esse chute está certo?
Primeiro, vamos calcular a vazão com esse K que veio da hipótese inicial.
Substituindo
Lembrando que
E encontramos essa vazão volumétrica
Passo 3
Para saber se nossa hipótese está certa, vamos utilizar esse valor de Q para calcular o Reynolds. Se der maior que , então acertamos!
Como , então a hipótese está certa e
Como ela está sendo pedida em , vamos converter
Encontramos a vazão volumétrica 😉
Resposta
Exercício Resolvido #4
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 431, ex. P 6.150
Gasolina a 20°C escoa a por um tubo de 15 cm de diâmetro e é medida por um medidor do tipo bocal de raio longo de 9 cm. Qual é a queda de pressão esperada através do bocal?
Passo 1
Vamos lá! Nesse exercício temos um medidor de vazão que é um bocal! Queremos calcular a a queda de pressão Δp. E quem já sabemos pelo enunciado?
“Tubo de 15 cm de diâmetro” significa que o diâmetro antes da medição é de 15 cm
Quando o enuciado fala “medidor do tipo bocal de raio longo de 9 cm”, sabemos que
Sabendo e , podemos calcular a razão β
Finalmente, para completar os dados: o fluido é a gasolina a 20°C, logo
Passo 2
Para calcular o Δp, utilizamos essa fórmula em medidores de vazão
Lembrando que e
Para calcular o valor de C, vamos usar a equação de correlação para bocais de raio largo.
Essa equação é válida para β entre 0,25 e 0,75 (é o nosso caso, pois nosso β é 0,6) e para entre e (precisamos calculá-lo e conferir!)