Princípio de Stevin e Manômetros
Produzido por Raphael EloiTeoria
O que Stevin disse?
Vimos como calcular a pressão hidrostática em um recipiente. Mas e se o recipiente for um tubo em “U”. Como calcular a pressão em ?
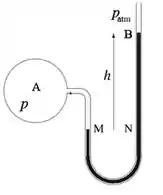
Bem, Stevin diz que a pressão em um mesmo fluido em repouso é igual em alturas iguais. Já falamos muito disso, não é mesmo? Afinal de contas, a equação que deduzimos para a pressão hidrostática em um ponto devido a coluna de fluido acima do ponto é dada por:
Ou seja: depende apenas da altura para um mesmo fluido. E pra que esse princípio serve?
Vamos usar esse princípio para resolver muitas questões, com um simples passo:
Escolher dois pontos na mesma altura e mesmo líquido para igualar as pressões.
Na mesma altura e no mesmo líquido! Essas regras são muito importantes para usar o Princípio de Stevin.
Tá, mas como assim? Olha a figura lá em cima, a gente quer descobrir a pressão na região .
Para isso basta escolher dois pontos, no mesmo fluido e na mesma altura e igualar as pressões.
Os pontos escolhidos são:
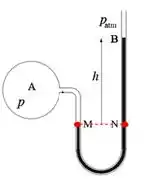
No ponto a esquerda (M) a única pressão acima dele é a pressão que é a pressão na região . Logo, nesse caso:
E aí o que você tem que pensar é que nesse recipiente esférico da esquerda (nessa bola) tem um gás com certa pressão, e esse gás desce pelo tubo até o ponto M. Por isso a pressão em A é igual à pressão em M.
Já no ponto à direita (N) a pressão desse ponto é a pressão exercida pela pressão atmosférica mais a pressão da coluna de líquido.
Assim, a pressão no ponto é
Beleza, escolhemos os dois pontos, agora basta igualar as pressões
E assim:
A beleza nisso é que sabendo a pressão de um lado conseguimos descobrir a pressão do outro lado. Com isso, podemos resolver muitos problemas, tipo quase todos!

E além disso, com esse exemplo acabei de te mostrar o que é um manômetro! O nome é estranho, mas viu, não é um bicho de sete cabeças.
Manômetros
Manômetro é um instrumento que tem a função de medir diferenças de pressões. Ué, diferença? Como assim?
No caso acima, medimos a diferença de pressão de um lugar (região ) em relação a pressão atmosférica (pois o outro lado é aberto).
Mas e se o outro lado fosse fechado?
Como por exemplo, nesse estilo:
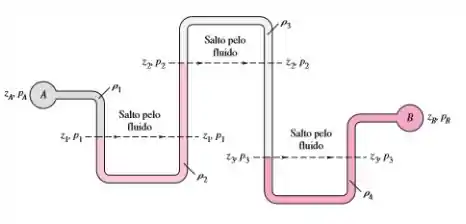
Bem mais complexo, né? Para calcular a diferença de pressão entre A e B, a gente poderia ir aplicando o Princípio de Stevin em vários pares de ponto, até encontrar a resposta.
Mas concorda que nesse caso, aplicar Stevin várias vezes vai dar trabalho? É, daria mesmo. A boa notícia é que tem uma outra técnica que é mais simples de resolver esse tipo de problema.
Vou te mostrar essa maravilha que vai nos salvar. Relembrando, o que queremos saber?

E tudo que estamos estudando aqui está estático né?!
Então vamos usar a pouco famosa segunda lei de Newton
Mas força? Não estávamos trabalhando com pressão? Esse é o pulo do gato, se todo o manômetro manter o mesmo calibre (área). Podemos transformar a equação de força em pressão.
Como , podemos escrever:
Se por todo o percurso a área for a mesma, podemos cortar ela da equação, assim, chegando em:
Então vamos começar a montar a equação de pressão da seguinte forma:
Passo a Passo: Para achar a diferença de pressão em tubos fechados
Vou te explicar esse passo a passo mostrando um exemplo! Então, vamos lá, queremos calcular a diferença de pressão entre as extremidades A e B da figura a seguir:
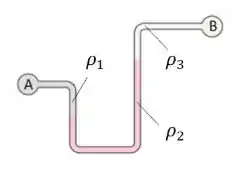
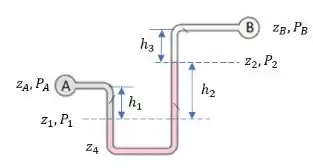
Passo 1 - Escolhemos uma extremidade para partir (pode ser qualquer uma delas! Você que escolhe). Exemplo: escolhemos a extremidade A.
Passo 2 - Percorremos o caminho até a outra extremidade. Começamos a escrever a equação
Comece colocando a pressão do ponto inicial escolhido:
Calma, jovem! A gente vai completar a equação ao longo desse passo a passo!
Passo 3 – Vamos seguir o caminho em direção a outra extremidade do tubo.
Como escolhemos começar pela extremidade A, o caminho é esse aqui, indicado com as setinhas:
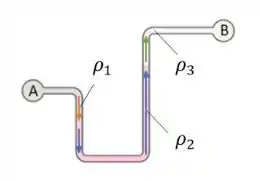
Para cada coluna de líquido que percorremos neste caminho, nós adicionamos (ou subtraímos) o valor da pressão dessa coluna de líquido na nossa equação.
Se a gente adiciona ou subtrai, como eu sei o sinal da pressão então?
Trago uma boa notícia! Tem uma regra simples para saber isso:
Se a coluna está descendo no nosso caminho, o sinal é positivo
Se a coluna está subindo no nosso caminho, o sinal é negativo
Ah, legal, muito maneiro que dá pra saber o sinal, né! Mas o sinal de quem mesmo?
Já te respondo: é o sinal da pressão da coluna de líquido, que na estática dos fluidos é descrita por:
No nosso exemplo, como isso fica? Relembrando, nossa equação está assim até agora:
Agora, temos uma coluna do líquido de densidade descendo. Logo, nossa equação fica assim:
Repara que o sinal de + é porque tá descendo! A partir de agora, temos que aplicar essa mesma lógica, até chegarmos em B.
A próxima coluna de líquido é a rosa. Veja que esse fluido desce e depois sobe. Podemos calcular a pressão desse fluido descendo e depois subindo, mas isso daria mais trabalho. Então, quando o fluido sobe e desce (ou desce e sobe) você pode pegar um atalho!
Atalhos para fluidos que sobem e descem (ou descem e sobem)
Bem, se o fluido descesse e depois subisse na mesma altura, nós íriamos somar a pressão descendo e subtrair a pressão subindo e o resultado seria zero!
Então! O nosso fluido rosa desce de até . Depois ele sobe de até . E depois sobe de até .
Ou seja, as pressões subindo e descendo entre e se cancelam! É como se o nosso fluido só tivesse subindo de até .
Logo, como é uma subida, o sinal é negativo:
E assim, na nossa equação da pressão:
Opa, show de bola! Tá faltando só mais um fluido no nosso caminho, o fluido 3. Ele tá só subindo. Então...
Atualizando a equação da pressão:
Passo 4 – Chegamos na outra extremidade! Uhul! Finalmente!
Então agora nós fechamos a nossa equação da pressão subtraindo a pressão no ponto B. E igualando a zero!
Ufa! Chegamos no final do caminho! Se conhecermos as alturas e as massas específicas de cada fluido podemos determinar a diferença de pressão entre A e B. No nosso exemplo, ficou assim:
Bora ver um resumão desse passo a passo?
Passo 1 - Escolhemos uma extremidade para partir.
Passo 2 - Percorremos o caminho até a outra extremidade. Começamos a escrever a equação Comece colocando a pressão do pressão do ponto inicial escolhido
Passo 3 - Vamos seguir o caminho em direção a outra extremidade do tubo. Na nossa equação vamos acrescentando as pressões das colunas de líquido.
Se a coluna está descendo no nosso caminho, o sinal é positivo
Se a coluna está subindo no nosso caminho, o sinal é negativo
Passo 4 - Subtraímos a pressão da outra extremidade na equação e igualamos a zero a expressão.
Agora que vimos as formas de calcular pressão e diferença de pressão utilizando Stevin e o passo a passo de tubo fechado, vamos fazer uns exercícios? o/