Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Balanço Diferencial de Massa

Ver Todos os Exercícios

Teoria

A gente viu no balanço integral de massa como que a gente pode fazer pra calcular, por exemplo, a concentração média de um sistema depois de um tempo t . Mas e se agora a gente quiser saber essa mesma concentração, mas especificamente em um espacinho dentro do nosso volume de controle?

Bom, pra isso a gente precisa de um balanço diferencial, que vai avaliar as propriedade pra cada dx e dy hahaha.

Vamos ver como fazer isso?

Construindo o Balanço de Massa

Vamos começar olhando então o que seria um volume de controle diferencial:

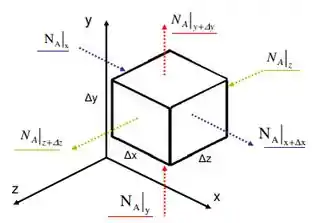
Imagina que esse ∆ x , ∆ y e ∆ z sejam beeeem pequenininhos.

Vamos analisar dx!

A taxa de fluido que passa por dx é o fluxo de massa em x, N A , x , vezes a área ∆ y ∆ z (porque taxa = fluxo x área, lembra?). Maaas, não necessariamente tudo que entra por esse ∆ x sai desse ∆ x ! Então, a gente diz que a taxa líquida vai ser:

N A , x + ∆ x ∆ y ∆ z - N A , x ( ∆ y ∆ z )

Isso só em relação a x, essa mesma taxa pode ser calculada em relação à ∆ y e ∆ z .

Beleza, mas se o que entra for maior do que o que sai, eu vou ter alguma coisa e acumulando ali, certo? Certo!

No balanço integral a gente representou dessa forma:

d d t ∫ V c A ( t ) ρ A d V

Aqui no diferencial, a gente vai considerar o volume de controle constante, porque esse espacinho que estamos analisando não vai mudar. E além disso, como nosso volume de controle é muito pequeno, podemos considerar a concentração mássica constante também em todo o espaço. Dai nosso termo fica assim:

d ρ A d t ( ∆ x ∆ y ∆ z )

Beleza, agora a única coisa que falta a gente considerar, que nem a gente fez no balanço integral é quando está acontecendo alguma reação no nosso volume de controle.

- r A ( ∆ x ∆ y ∆ z )

Obs.: Esse sinal vai depender se A é reagente ou produto! Considerando A reagente, ele vai ser consumido ao longo do tempo, logo o sinal é negativo!

Vale lembrar que, assim como no balanço integral, as unidades de todos os termos ficam como massa por unidade de tempo.

Enfim o nosso balanço em relação à x:

N A , x + ∆ x ∆ y ∆ z - N A , x ∆ y ∆ z + d ρ A d t ∆ x ∆ y + r A ∆ x ∆ y ∆ z = 0

Dividindo tudo pelo volume ( ∆ x ∆ y ∆ z ):

N A , x + ∆ x - N A , x ∆ x + d ρ A d t - r A = 0

Mas esse primeiro termo ai ainda dá pra mexer um pouco nele, fazendo o limite com ∆ x tendendo a zero, a gente tem justamente a derivada de N A em relação a x!

Finalmente, pra você guardar no coração:

∇ N A + d ρ A d t - r A = 0

Lembrando que:

∇ N A = ∂ N A ∂ x + ∂ N A ∂ y + ∂ N A ∂ z

Outros jeitos de usar esse balanço

Bom, a gente acabou de ver o nosso balanço diferencial mássico, mas e se no problema os dados que eu tiver estiverem em função de molaridade?

Reescrevendo nosso balanço em termos molares:

∇ N A M + d C A d t   - r A M = 0

O índice M é para indicar que as unidades estão em função de mol.

Se a gente lembrar também das correlações que vimos nos fundamentos da transferência de massa, esse balanço pode ter várias outras caras:

∇ N A + ρ d w A d t - r A = 0

∇ ( ρ A . v A ) + d ρ A d t - r A = 0

∇ ρ A . v + j A + d ρ A d t - r A = 0

Sabendo também que j A =   - D A B ∇ ρ A

d ρ A d t + ∇ ρ A . v - D A B ∇ ρ A - r A = 0

Se D A B for constante:

d ρ A d t + ∇ ρ A . v = D A B ∇ ² ρ A + r A

E para um sistema binário?

Para um sistema binário nós podemos somar esse mesmo balanço para o componente A, com um similar para o componente B!

∇ N A + N B + ∂ ( ρ A + ρ B ) ∂ t - r A + r B = 0

∇ ρ . v + ∂ ρ ∂ t - r A + r B = 0

Em termos molares:

∇ C . v M + ∂ C ∂ t - r A M + r B M = 0

E em outras coordenadas?

Nem sempre a difusão vai estar acontecendo em coordenadas cartesianas x, y e z. Vamos ver como fica a expressão pra coordenadas cilíndricas e esféricas:

  • Em coordenadas cilíndricas:

    • ∇ N A = 1 r ∂ ( r N A , r ) ∂ r + 1 r ∂ N A , θ ∂ θ + ∂ N A , z ∂ z

  • Em coordenadas esféricas:

∇ N A = 1 r ² ∂ ( r ² N A , r ) ∂ r + 1 r s e n θ ∂ ( s e n θ N A , θ ) ∂ θ + 1 r s e n θ ∂ N A , φ ∂ φ

Caaaalma gafanhoto, agora a gente vai ver como que a gente pode simplificar isso ai:

Vamos pegar a versão completa

d ρ A d t + ∇ ρ A v = D A B ∇ ² ρ A + r A

E fazer nossas hipóteses:

  1. Fluido incompressível ( ρ = c o n s t a n t e ) e com D A B constante também:

    2. ∂ ρ A ∂ t + v ∇ ρ A = D A B ∇ 2 ρ A + r A

    Essa simplificação vem lá do balanço global. E esse lado esquerdo todo da equação é o que a gente chama de derivada material. Dai a expressão fica com essa cara:

    D ρ A D t = D A B ∇ 2 ρ A + r A

  2. Sem reação química ( r A = 0 ):

    3. D ρ A D t = D A B ∇ 2 ρ A

    Essa expressão se assemelha àquela de transcal D T D t = α ∇ ² T . É o que a gente chama de 2ª lei de Fick da difusão.

  3. Sem escoamento, o fluido não está em movimento:

    4. ∂ ρ A ∂ t = D A B ∇ 2 ρ A + r A

    Essa é a equação da difusão transiente que a gente vai ver mais pra frente!

  4. Estado estacionário ∂ ρ A ∂ t = 0 :

v ∇ ρ A = D A B ∇ 2 ρ A + r A

Sem reação:

v ∇ ρ A = D A B ∇ 2 ρ A

Sem escoamento:

∇ 2 ρ A = 0

Esse último chamamos de difusão pura.

Ufa, acabou! Agora bora praticar!

Outros jeitos de usar esse balanço

E para um sistema binário?

E em outras coordenadas?

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Enuncie o balanço de massa diferencial para um sistema com 3 componentes.

Passo 1

O balanço diferencial pra um componente tem essa cara:

∇ N A + d ρ A d t - r A = 0

Considerando 3 componentes ele fica:

∇ ( N A + N B + N C ) + d ( ρ A + ρ B + ρ C ) d t - ( r A + r B + r C ) = 0

Resposta

∇ ( N A + N B + N C ) + d ( ρ A + ρ B + ρ C ) d t - ( r A + r B + r C ) = 0

Exercício Resolvido #2

Elaboração Própria

Usando o balanço diferencial de massa na sua versão explicidada d ρ A d t + ∇ ρ A v = D A B ∇ 2 ρ A + r A

Mostre quais são as possíveis simplificações para essa equação.

Passo 1

Analisando cada termo da equação completa:

d ρ A d t + ∇ ρ A v = D A B ∇ 2 ρ A + r A

  1. Sem reação: d ρ A d t + ∇ ρ A v = D A B ∇ ² ρ A
  2. Sem escoamento: d ρ A d t = D A B ∇ ² ρ A + r A
  3. Estado estacionário: ∇ ρ A v = D A B ∇ ² ρ A + r A

Resposta

  1. d ρ A d t + ∇ ρ A v = D A B ∇ ² ρ A

  2. d ρ A d t = D A B ∇ ² ρ A + r A

  3. ∇ ρ A v = D A B ∇ ² ρ A + r A

Exercício Resolvido #3

Elaboração Própria

Mostre o termo espacial do balanço diferencial nas seguintes coordenadas:

  1. Cartesianas
  2. Cilíndricas
  3. Esféricas

Passo 1

O balanço diferencial é composto de um termo espacial, um termo temporal e um termo de reação: ∇ N A + d ρ A d t - r A = 0

O termo espacial é o gradiente de N A , que descreve o fluxo em todo espaço. Explicitando suas coordenadas temos:

  1. Cartesianas ∇ N A = ∂ N A ∂ x + ∂ N A ∂ y + ∂ N A ∂ z
  2. Cilíndricas ∇ N A = 1 r ∂ ( r N A , r ) ∂ r + 1 r ∂ N A , θ ∂ θ + ∂ N A , z ∂ z
  3. Esféricas ∇ N A = 1 r ² ∂ ( r ² N A , r ) ∂ r + 1 r s e n θ ∂ ( s e n θ N A , θ ) ∂ θ + 1 r s e n θ ∂ N A , φ ∂ φ

Resposta

  1. ∇ N A = ∂ N A ∂ x + ∂ N A ∂ y + ∂ N A ∂ z

  2. ∇ N A = 1 r ∂ ( r N A , r ) ∂ r + 1 r ∂ N A , θ ∂ θ + ∂ N A , z ∂ z

  3. ∇ N A = 1 r ² ∂ ( r ² N A , r ) ∂ r + 1 r s e n θ ∂ ( s e n θ N A , θ ) ∂ θ + 1 r s e n θ ∂ N A , φ ∂ φ

Exercício Resolvido #4

Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 24 (Adaptado)

O desenho a seguir ilustra a difusão de gás dentro da vizinhança de uma superfície catalítica lisa. Gases quentes de hidrocarbonetos pesados difundem para a superfície catalítica onde eles são craqueados em componentes mais leves pela reação: H → 2 L , os produtos leves difundem de volta para a corrente de gás.

  1. Reduza a equação diferencial deral de transferência de massa para a reação específica que descreve esse processo no estado estacionário. Liste as hipóteses assumidas para fazer as simplificações.
  2. Determine a relação da Lei de Fick em termos do componente H e insira isso na equação diferencial obtida na letra (a).

Passo 1

Vamos resolver então a letra a, que ele pede a equação simplificada!

Temos que:

∇ N A + d C A d t   - r A = 0

Nossas hipóteses são, pelos dados do problema:

  1. Estado estacionário d C A d t   = 0
  2. Sem reação homogênea ( r A = 0 )
  3. Coordenadas cartesianas   ∇ N A = ∂ N A ∂ x + ∂ N A ∂ y + ∂ N A ∂ z
  4. Fluxo unidimensional no eixo z ∂ N A ∂ x = ∂ N A ∂ y = 0

A quação simplificada fica então:

d N A d z = 0

Ou seja, nosso fluxo ao longo do eixo z é constante!

Passo 2

Pra letra b o problema quer que a gente relacione a Lei de Fick na expressão que encontramos na letra A. A Lei de Fick é a que descreve o fluxo de massa, então vamos dar uma olhada aqui na expressão que a gente tem:

N A =   J A + y A ∑ i = A n N i

Abrindo aquele J A da Lei de Fick:

N A =   - D A M ∇ C A + y A ∑ i = A n N i

Agora vamos colocar em termos do nosso problema!

N H =   - D H L ∇ C H + y H ( N H + N L )

Passo 3

Pela estequiometria temos que N H = 2 N L , então:

N H =   - C D H L d y H d z + y H N L 2

N H =   - C D H L ( 1 - y H / 2 ) d y H d z

N H d z =   - C D H L ( 1 - y H / 2 ) d y H

Como na letra (a) encontramos que o fluxo é constante, podemos integrar e colocar N para fora da integral!Integrando então ambos os lados:

N H δ - 0 =   - C D H L   l n ( 1 - y H / 2 ) | y H 0 y H δ

N H =   C D H L δ   l n 1 - y H 0 1 - y H δ

Resposta

  1. d N A d z = 0
  2. N H =   C D H L δ   l n 1 - y H 0 1 - y H δ

Exercício Resolvido #5

Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 25

Uma gotícula de água repousando em uma superífice plana, com formato semiesférico, evapora através de difusão molecular através do ar inerte ao seu redor. A gotícula inicialmente tem raio R. Conforme o líquido evapora lentamente, a gotícula encolhe com o tempo, mas o fluxo de vapor de água está em estado estacionário. A temperatura da gota e dos arredores é mantida constante. O ar contém vapor de água à uma infinida distância da superfície de gota.

  1. Selecione um sistema de coordenadas que melhor descreve esse processo de difusão. Liste pelo menos 5 hipóteses razoáveis para o processo de transferência de massa da evaporação da água e simplifique a equação diferencial geral em termos do fluxo N A .
  2. Qual é a forma simplificada e diferencial da equação de Fick para o vapor de água (espécie A)?

Passo 1

Vamos resolver então a letra a!

Para esse caso o melhor tipo de coordenadas são esféricas, já que estamos falando de uma meia esfera. Vamos agora simplificar a equalção geral.

Temos que:

∇ N A + d C A d t   - r A = 0

As hipóteses que podem ser assumidas:

  1. Estado estacionário d C A d t   = 0
  2. Sem reação homogênea ( r A = 0 )
  3. Coordenadas esféricas

    4. ∇ N A = 1 r ² ∂ ( r ² N A , r ) ∂ r + 1 r s e n θ ∂ ( s e n θ N A , θ ) ∂ θ + 1 r s e n θ ∂ N A , φ ∂ φ

  4. Fluxo unidimensional no eixo radial ∂ s e n θ N A , θ ∂ θ = 1 r s e n θ ∂ N A , φ ∂ φ = 0
  5. Espérie B (Ar) estagnada, não se mistura em A ( N B = 0 )
  6. Pressão e Temperatura constantes ( D A B = c t e ,   C = c t e )

A equação simplificada fica então:

1 r ² ∂ ( r ² N A , r ) ∂ r = 0

∂ ( r ² N A , r ) ∂ r = 0

Ou seja, r ² N A , r = c t e !

Passo 2

Pra letra b o problema quer que a gente encontre a equação de Fick diferencial e simplificada pra espécie A.

N A =   J A + y A ∑ i = A n N i

Abrindo aquele J A da Lei de Fick:

N A =   - D A M ∇ C A + y A ∑ i = A n N i

Agora vamos colocar em termos do nosso problema!

N A =   - C D H L ∇ y A + y A N A

Passo 3

Rearranjando os termos:

N A =   - C D H L ( 1 - y A ) d y A d r

N A d r =   - C D H L ( 1 - y A ) d y A

Como na letra (a) encontramos que r ² N A , r = c t e é constante, vamos multiplicar o termo da esquerda por r ² r ² para podermos conseguir integrar!

∫ r ² r ² N A d r =   ∫ - C D H L ( 1 - y A ) d y A

r ² N A ∫ 1 r ² d r =   ∫ - C D H L ( 1 - y A ) d y A

Integrando então ambos os lados:

N A , r =   C D A B r   l n 1 - y A R 1 - y A 0

Resposta

  1. ∂ ( r ² N A , r ) ∂ r = 0
  2. N A , r =   C D A B r   l n 1 - y A R 1 - y A 0

Exercício Resolvido #6

Welty, J. R., Wicks, C. E., Wilson, R. E., Rorrer, G. L. (2008), Fundamentals of Momentum, Heat and Mass Transfer, 5th edition, John Wiley & Sons, New Jersey, chapter 25

A umidade em ar quente, úmido e estagnado ao redor de uma tubulação de água gelada difunde continuamente até a superfície fria onde ela condensa. A água condensada forma um filme líquido ao redor do cano, e então pinga continuamente no chão. A uma distância de 10 cm da superfície do cano, o teor de umidade do ar é constante. Perto do cano, o teor de umidade aproxima a pressão de vapor da água avaliada na temperatura do cano.

  1. Selecione um sistema de coordenadas que melhor descreve esse processo de difusão. Liste pelo menos 5 hipóteses razoáveis para o processo de transferência de massa da condensação da água.
  2. Qual é a forma simplificada da equação diferencial geral de transferência de massa em termos do fluxo de vapor d’água, N A ?
  3. Qual é a forma diferencial simplificada da equação de Fick para o vapor de água, N A ?
  4. Qual é a forma simplificada da equação diferencial geral de transferência de massa em termos da concentração de vapor d’água, C A ?

Passo 1

Vamos resolver então a letra a!

Para esse caso o melhor tipo de coordenadas são cilíndricas, já que estamos falando de uma tubulação!

As hipóteses que podem ser assumidas:

  1. Estado estacionário d C A d t   = 0
  2. Sem reação homogênea ( r A = 0 )
  3. Coordenadas esféricas

    4. ∇ N A = 1 r ∂ ( r N A , r ) ∂ r + 1 r ∂ N A , θ ∂ θ + ∂ N A , z ∂ z

  4. Fluxo unidimensional no eixo radial 1 r ∂ N A , θ ∂ θ = ∂ N A , z ∂ z = 0
  5. Espérie B (Ar) estagnada, não se mistura em A ( N B = 0 )
  6. Pressão e Temperatura constantes ( D A B = c t e ,   C = c t e )

Passo 2

Letra b, vamos simplificar a equalção geral.

Temos que:

∇ N A + d C A d t   - r A = 0

A equação simplificada fica então:

1 r ∂ ( r N A , r ) ∂ r = 0

∂ ( r N A , r ) ∂ r = 0

Ou seja, r N A , r = c t e !

Passo 3

Pra letra c o problema quer que a gente encontre a equação de Fick diferencial e simplificada pra espécie A.

N A =   J A + y A ∑ i = A n N i

Abrindo aquele J A da Lei de Fick:

N A =   - D A M ∇ C A + y A ∑ i = A n N i

Agora vamos colocar em termos do nosso problema!

N A =   - C D H L ∇ y A + y A N A

Rearranjando os termos:

N A =   - C D H L ( 1 - y A ) d y A d r

N A d r =   - C D H L ( 1 - y A ) d y A

Como na letra (a) encontramos que r N A , r = c t e é constante, vamos multiplicar o termo da esquerda por r r para podermos conseguir integrar!

∫ r r N A d r =   ∫ - C D H L ( 1 - y A ) d y A

r N A ∫ 1 r d r =   ∫ - C D H L ( 1 - y A ) d y A

Integrando então ambos os lados:

N A , r =   C D A B r   l n R + 10 R   l n 1 - y A r 1 - y A v

Passo 4

Agora pra letra (d) só precisamos passar os termos em função da fração molar pra concentração!

y A = C A C

Logo,

N A , r =   C D A B r   l n R + 10 R   l n 1 - C A C 1 - C A V C

Resposta

  1. Coordenadas cilíndricas
  2. ∂ r N A , r ∂ r = 0
  3. N A , r =   C D A B r   l n R + 10 R   l n 1 - y A r 1 - y A v
  4. N A , r =   C D A B r   l n R + 10 R   l n 1 - C A C 1 - C A V C

Exercício Resolvido #7

Transferência de calor e massa - 4ª Edição - Çengel e Ghajar

A eficácia de produtos farmacêuticos é reduzida pela exposição prolongada a altas temperaturas, à luz e à umidade. Para produtos consumidos que são sensíveis ao vapor de água e encontram-se na forma de comprimidos ou cápsulas e são guardados em ambientes úmidos, como armários de banheiro, embalagens blister são usadas para limitar a exposição direta do medicamento às condições de umidade até o momento imediatamente anterior ao seu uso.

Considere comprimidos que estão contidos em uma embalagem blister composta por uma folha de cobertura plana e uma segunda folha moldada, que tem compartimentos que abrigam cada comprimido. A folha moldada tem espessura L   =   50   μ m e é fabricada com um material polimérico. Cada compartimento tem diâmetro D   =   5   m m e profundidade h   =   3   m m . A folha de cobertura é feita de alumínio. O coeficiente de difusão binária do vapor de água no polímero é D A B = 6 ⋅ 10 - 14   m 2 / s , enquanto pode-se supor que o alumínio seja impermeável em relação ao vapor de água. Para concentrações molares do vapor de água no polímero nas superfícies externa e interna de C A ,   S 1 = 4,5 ⋅ 10 - 3   k m o l / m ³ e C A ,   S 2 = 0,5 ⋅ 10 - 3   k m o l / m ³ , respectivamente, determine a taxa na qual o vapor de água é transferido através da parede do compartimento para o comprimido.

Passo 1

E aí? Tudo show de bolinhas? Vamos resolver essa questãozinha aí juntinhos? Partiu!!

O nosso enunciado quer a taxa na qual o vapor de água transferido N A ,   x