Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Balanço Integral de Massa

Ver Todos os Exercícios

Teoria

O Balanço de Massa é baseado na lei de conservação de massa, de Lavoisier. Com certeza você já ouviu que “Na natureza nada se cria, nada se perde, tudo se transforma”. Então, é esse o espirito da coisa!

Então vamos começar considerando o seguinte sistema genérico abaixo:

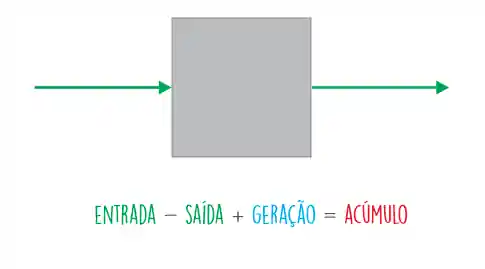
Balanço de massa
Balanço de massa

Essa caixinha pode ser qualquer coisa, mas aqui vamos imaginar que ele é um reator químico. Vamos ter uma corrente entrando, lá dentro vai ocorrer uma reação química e depois a corrente irá sair!

O balanço de massa é dado pela fórmula que vimos ali em cima, que é beeem simples e ela vai ser muito útil em muitos casos! Mas sinto lhe informar que na prova, muito provavelmente, não vai ser essa fórmula que vai cair! 🥲🥲🥲

Antes de irmos pra fórmula que vamos usar de fato, precisamos entender muito bem a geometria do problema! Bora lá?

Volume de Controle

O volume de controle é a região do espaço que estamos analisando! Por exemplo, ali em cima vimos alguma coisa entrando e saindo de uma caixinha, então podemos dizer que o volume de controle é um cubo!

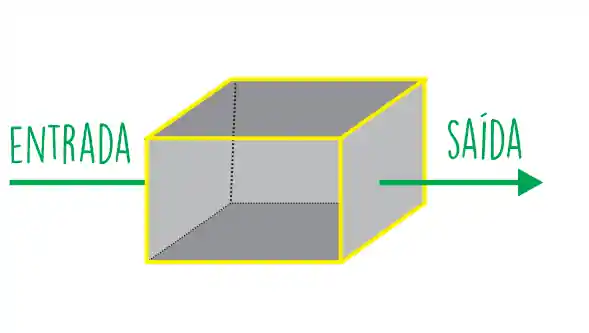
Volume de controle
Volume de controle

O volume de controle é uma região delimitada, mas esse limite pode ser físico como por exemplo, as paredes de um reator. Ou imaginário, nesse caso cabe a você delimitar a geometria mais coerente e conveniente pra resolver o problema!

Podemos também definir a superfície de controle:

Superfície de Controle
Superfície de Controle

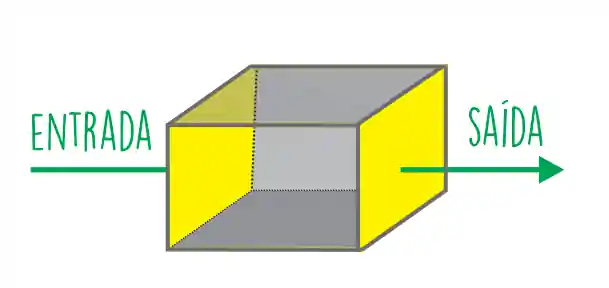
📢 Clique para ver mais:

Balanço Integral de Massa

O balanço integral de massa vem do Teorema de Transporte de Reynolds. Ele é baseado na conservação de massa, momento e energia! A equação do balanço integral de massa tem essa cara aqui:

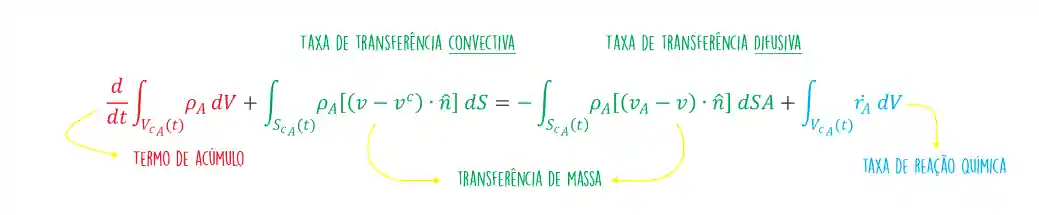
Balanço Integral de Massa
Balanço Integral de Massa

Aqui os termos de entrada e saída se dividem em dois tipos, levando em conta a transferência de massa pelo mecanismo convectivo e difusivo. Agora, bora destrinchar todos esses termos e entender como usar cada um?! 😍

Termos de Entrada e Saída - Transferência de Massa

Como vimos ali em cima, os termos de entrada e saída se dividem em dois tipos. A transferência de massa envolvendo o mecanismo difusivo e o mecanismo convectivo

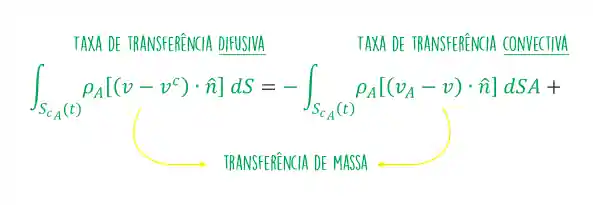
Transferência de Massa
Transferência de Massa

Você também pode conferir esse conteúdo em vídeo:

Termo de Acúmulo: Regime Permanente e Regime Transiente

O termo de acúmulo sempre acompanha uma derivada em relação ao tempo, então é bem tranquilo de identificar ele!

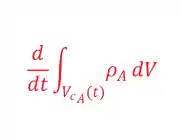
Balanço Integral de Massa: termo de acúmulo
Balanço Integral de Massa: termo de acúmulo

Ele só é usado em regimes transientes, ou seja, quando há variação de massa dentro do volume de controle ao longo do tempo. Em problemas permanentes esse termo pode ser cortado!

Termos de Geração e Consumo: Balanço de Massa com Reação Química

Em problemas envolvendo reações químicas, precisamos usar o termo de reação:

Balanço integral de massa: Termo de reação
Balanço integral de massa: Termo de reação

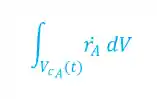
O r na equação acima vem da lei de velocidade de reação química. Se a reação tiver consumindo a substância analisada no BM, então esse termo será negativo e se ela estiver formando, o termo de reação será positivo.

Como fazer o Balanço de Massa Passo a Passo

Agora que conhecemos todos os termos do balanço integral de massa, vamos ver qual é o passo a passo para resolver um problema!

Passo 1: Definir a Geometria do Problema

Nesse passo definimos o volume de controle e a superfície de controle!

Passo 2: Fazer Simplificações

Verificar se o problema é permanente, transiente e se tem reação química. No caso de um problema em regime permanente e sem reação, podemos cortar o termo de acúmulo e de reação.

Nesse passo podemos verificar qual é o mecanismo de transferência de massa predominante. Por exemplo, no caso do mecanismo convectivo de transferência o predominante, podemos cortar o termo relacionado ao mecanismo difusivo.

Passo 3: Analisar as expressão termo a termo, usando essas simplificações

Nessa etapa analisamos os dados que temos em mãos e vemos se temos todos os dados necessários.

Passo 4: Juntar tudo e resolver o problema

Agora a gente só precisa fazer os cálculos e prontinho! Vamos praticar esse passo a passo nos exercícios?

Como fazer o Balanço de Massa Passo a Passo

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Enuncie a equação da Conservação de Massa e explique o que cada termo representa.

Passo 1

A equação da Conservação de Massa tem essa cara aqui:

d d t ∫ V c ( t ) ρ   d V + ∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S = 0

d d t ∫ V c ( t ) ρ   d V é o termo que descreve a variação de massa dentro do volume de controle.

∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S é o termo que descreve o que está entrando no volume de controle através da velocidade da espécie v menos o que está saindo do volume de controle através da velocidade do fluido v ∞ .

Sendo assim, a variação do volume é igual ao que entra menos o que sai!

Resposta

d d t ∫ V c ( t ) ρ   d V - descreve a variação de massa dentro do volume de controle.

∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S - descreve o que está entrando no volume de controle através da velocidade da espécie v menos o que está saindo do volume de controle através da velocidade do fluido v ∞ .

Exercício Resolvido #2

Elaboração Própria

Enuncie a equação da Conservação de Quantidade de Movimento e explique o que cada termo representa.

Passo 1

A equação da Conservação de Quantidade de Movimento tem essa cara aqui:

d d t ∫ V c ( t ) ρ v   d V + ∫ S c ( t ) ρ v v - v ∞ ∙ n ^   d S =   ∫ S c ( t ) τ ∙ n ^   d S + ∫ V c ( t ) ρ f m   d V

d d t ∫ V c ( t ) ρ v   d V é o termo que descreve a variação de momento linear a dentro do volume de controle.

∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S é o termo que descreve o que está o aumento do momento através da espécie que entra na superfície com velocidade v menos o momento que está sendo perdido através das espécies que saem com a velocidade do fluido v ∞ .

∫ S c ( t ) τ ∙ n ^   d S é o termo que descreve as forças de superfície, como as forças de atrito com a parede, que são perdidas através do movimento do fluido.

∫ V c ( t ) ρ f m   d V é o termo que descreve as forças volumétricas, como a gravidade, que pode gerar o acúmulo de uma espécie específica em uma região do volume de controle.

Sendo assim, a variação da quantidade de movimento é igual à soma de todos os fatores que podem estar associados a perda de massa ou velocidade do volume de controle.

Resposta

d d t ∫ V c ( t ) ρ v   d V - descreve a variação de momento linear a dentro do volume de controle.

∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S - descreve o que está o aumento do momento através da espécie que entra na superfície com velocidade v menos o momento que está sendo perdido através das espécies que saem com a velocidade do fluido v ∞ .

∫ S c ( t ) τ ∙ n ^   d S - descreve as forças de superfície, como as forças de atrito com a parede, que são perdidas através do movimento do fluido.

∫ V c ( t ) ρ f m   d V - descreve as forças volumétricas, como a gravidade, que pode gerar o acúmulo de uma espécie específica em uma região do volume de controle.

Exercício Resolvido #3

Elaboração Própria

Enuncie a equação do Balanço Integral de Massa e explique o que cada termo representa.

Passo 1

O balanço integral de massa tem essa cara aqui:

d d t ∫ V c A ( t ) ρ A d V + ∫ S c A ( t ) ρ A v - v c ∙ n ^   d S = - ∫ S c A t ρ A v A - v ∙ n ^   d S + ∫ V c A ( t ) r A ˙   d V

d d t ∫ V c ( t ) ρ   d V é o termo que descreve a variação de massa a dentro do volume de controle.

∫ S c ( t ) ρ v - v c ∙ n ^ d S é o termo que descreve a massa que está entrando no volume de controle através da velocidade da espécie v menos o que está saindo do volume de controle através da velocidade do fluido v ∞ .

∫ S c A t ρ A v A - v ∙ n ^   d S é o termo que descreve a taxa de espécie A que atravessa a superfície de controle S C A pelo mecanismo difusivo.

∫ V c A ( t ) r A ˙   d V é o termo que descreve o quanto da espécie A “some” ou “aparece” devido a alguma reação homogênea que esteja acontecendo dentro do volume de controle.

Sendo assim, a variação de massa dentro do volume de controle é igual ao que entra menos o que sai por convecção, o que entra menos o que sai por difusão e o que aparece ou some devido a uma reação.

Resposta

d d t ∫ V c ( t ) ρ   d V - descreve a variação de massa a dentro do volume de controle.

∫ S c ( t ) ρ v - v c ∙ n ^ d S - descreve a massa que está entrando no volume de controle através da velocidade da espécie v menos o que está saindo do volume de controle através da velocidade do fluido v ∞ .

∫ S c A t ρ A v A - v ∙ n ^   d S - descreve a taxa de espécie A que atravessa a superfície de controle S C A pelo mecanismo difusivo.

∫ V c A ( t ) r A ˙   d V - descreve o quanto da espécie A “some” ou “aparece” devido a alguma reação homogênea que esteja acontecendo dentro do volume de controle.

Exercício Resolvido #4

Hauke, G. (2008), An Introduction to Fluid Mechanics and Transport Phenomena, 1st edition, Springer, Berlim, Chapter 6. (Adaptado)

Um tanque de volume 0,05   m ³ contem ar a pressão absoluta de p = 800   k P a e temperatura T = 15 ℃ . No tempo inicial, quanto t = 0 , a válvula abre e o ar escapa a uma velocidade de v = 311   m / s e densidade ρ = 6,13   k g / m ³ através de uma abertura de área A = 65   m m ² .

Qual é a taxa de mudança de densidade d ρ d t no tanque quando t = 0 ?

Passo 1

Bom, vamos então ver aquele passo a passo!

  1. Definir a geometria do problema: Volume de Controle e Superfície de Controle
  2. Montar o equacionamento do problema
  3. Fazer simplificações baseadas nas considerações que o problema te der
  4. Analisar a expressão termo a termo, usando essas simplificações
  5. Juntar tudo e resolver!

Passo 2

Vamos então definir a geometria do nosso problema!

O volume de controle vai ser então o volume que foi dado pelo problema.

V C = 0,05   m ³

A superfície de controle vai ser uma só, a área por onde o ar escapa quando a válvula é aberta.

S C = 65   m m 2 = 65   x   10 - 6   m ²

Passo 3

Vamos montar o balanço de massa então:

d d t ∫ V c A ( t ) ρ A d V + ∫ S c A ( t ) ρ A v - v c ∙ n ^   d S = - ∫ S c A t ρ A v A - v ∙ n ^   d S + ∫ V c A ( t ) r A ˙   d V

Como no nosso caso não está acontecendo transporte de espécie por difusão e nem está acontecendo reação química, a nossa equação se reduz à equação de conservação de massa:

d d t ∫ V c ( t ) ρ   d V + ∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S = 0

Outra simplificação que podemos considerar também é a densidade constante. Bora então resolver cada um desses termos!

Passo 4

Resolvendo o primeiro termo:

d d t ∫ V c ( t ) ρ   d V = V C d ρ d t = 0,05 d ρ d t

Pra resolver o segundo termo, consideramos v ∞ = 0 , já que não tem nenhum fluido externo fazendo arraste de matéria, quem está escoando é o próprio fluido do tanque. Sendo assim:

∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S = ρ v S C = 0,02 ρ

Passo 5

Juntando tudo temos que:

0,05 d ρ d t + 0,02 ρ = 0

Quando t = 0 :

d ρ d t = - 2,48   k g / m ³ s

Resposta

d ρ d t = - 2,48   k g / m ³ s

Exercício Resolvido #5

Hauke, G. (2008), An Introduction to Fluid Mechanics and Transport Phenomena, 1st edition, Springer, Berlim, Chapter 6. (Adaptado)

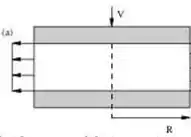
Dois discos planos de raio R são separados por uma distância b . O disco superior se move para baixo com velocidade constante V . O fluido entre os dicos é comprimido e escorre na direção radial. Determine a taxa volumétrica Q e a velocidade do fluido considerando o perfil de escoamento uniforme.

Passo 1

Bom, vamos então ver aquele passo a passo!

  1. Definir a geometria do problema: Volume de Controle e Superfície de Controle
  2. Montar o equacionamento do problema
  3. Fazer simplificações baseadas nas considerações que o problema te der
  4. Analisar a expressão termo a termo, usando essas simplificações
  5. Juntar tudo e resolver!

Passo 2

Vamos então definir a geometria do nosso problema!

O volume de controle vai ser então o espaço entre os dois discos de raio R, que vai ser um cilindro de altura b . V C = π R ² b ( t )

A superfície de controle vai ser uma só, é a superfície envolta do volume de controle, aonde o fluido está escoando. S C = 2 π R b ( t )

A gente não leva em consideração as superfícies de cima e de baixo do cilindro (que é como se fosse a parede do disco) porque ali não tem espécie atravessando, beleza?

Passo 3

Vamos montar o balanço de massa então:

d d t ∫ V c A ( t ) ρ A d V + ∫ S c A ( t ) ρ A v - v c ∙ n ^   d S = - ∫ S c A t ρ A v A - v ∙ n ^   d S + ∫ V c A ( t ) r A ˙   d V

Como no nosso caso não está acontecendo transporte de espécie por difusão e nem está acontecendo reação química, a nossa equação se reduz à equação de conservação de massa:

d d t ∫ V c ( t ) ρ   d V + ∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S = 0

Outra simplificação que podemos considerar também é a densidade constante. Bora então resolver cada um desses termos!

Passo 4

Resolvendo o primeiro termo:

d d t ∫ V c ( t ) ρ   d V = ρ d d t ∫ V c ( t )   d V = ρ d V C d t = ρ d π R ² b ( t ) d t = ρ π R ² d b t d t = - ρ π R ² v

Pra resolver o segundo termo, consideramos v ∞ = 0 , já que não tem nenhum fluido externo fazendo arraste de matéria, quem está escoando é o próprio fluido que estava entre os discos mesmo. E vamo chamar a velocidade do fluido de v f pra não confundir com a velocidade do disco que está descendo. Sendo assim:

∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S = ∫ S c ( t ) ρ ( v f ∙ n ^ ) d S = ρ v f 2 π R b ( t )

Passo 5

Juntando tudo temos que:

ρ π R 2 v =   ρ v f 2 π R b ( t )

Logo:

v f = v R 2 b ( t )

Com isso podemos calcular a tava volumétrica!

Passo 6

Calculando a taxa:

Q =   ∫ S v ^ · n ^   d S

Q =   ∫ S v f ^ · n ^   d S =   v R 2 b ( t ) x   2 π R b ( t )

Q = v π R ²

Resposta

v f = v R 2 b ( t )

Q = v π R ²

Exercício Resolvido #6

Hauke, G. (2008), An Introduction to Fluid Mechanics and Transport Phenomena, 1st edition, Springer, Berlim, Chapter 6. (Adaptado)

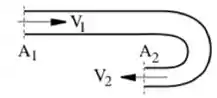
No cotovelo de 180˚ da figura circula agua que é descarregada na seção 2 para a atmosfera. A pressão do medidor é P = 96   k P a . As áreas são A 1 = 2600   m m ² e A 2 = 650   m m ² , a velocidade é V 1 = 3,05   m / s . Calcule a força F x para segurar o cotovelo.

Passo 1

Bom, pra essa questão vai ser melhor se a gente ver o equacionamento antes de começar a resolver. Com ele a gente vai vendo o que podemos simplificar e como vamos resolver cada coisa!

Como o problema está pedindo pra gente a força no eixo x, já é um indicativo de que vamos usar a equação da conservação da quantidade de movimento!

d d t ∫ V c ( t ) ρ v   d V + ∫ S c ( t ) ρ v v - v ∞ ∙ n ^   d S =   ∫ S c ( t ) τ ∙ n ^   d S + ∫ V c ( t ) ρ f m   d V

Passo 2

Vamos então ver o que que a gente pode cortar dai!

A gente vai considerar estado estacionário, porque o fluxo de água no cotovelo é contínuo, então não tem variação ao longo do tempo. Então, esse primeiro termo vai embora = 0 !

Fluido incompressível, então ρ = c o n s t a n t e .

v ∞ = 0 pois não tem nenhum fluido externo fazendo arraste de espécie.

E também vamos considerar f m = 0 , como se a gravidade não tivesse afetando nosso problema tanto assim, então o último termo vai embora também. (A gente pode fazer isso porque não tivemos nenhuma informação sobre esse termo).

Nosso balanço ficou então:

∫ S c t ρ v v ∙ n ^   d S =   ∫ S c t τ ∙ n ^   d S

Sendo que como temos duas áreas relevantes, a integral sobre a área vai ser a soma da integral pra A 1 e A 2 .

Passo 3

Vamos resolver cada termo então:

  ∫ S c t ρ v v ∙ n ^   d S = ∫ A 1 + A 2 ρ v v ∙ n ^   d S =   ρ V 1 2 A 1 + ρ V 2 2 A 2

Pela conservação de massas conseguimos achar V 2 :

A 1 V 1 = A 2 V 2

V 2 = 12,2   m / s

Assim:

∫ A 1 + A 2 ρ v v ∙ n ^   d S = - 24,18 + 96,75   N

Os sinais invertem porque o cotovelo faz 180˚ a gente orienta o vetor normal pra fora da superfície! Ou seja, pra A 1 a água está entrando e pra A 2 a água está saindo.

Passo 4

O outro termo é um pouco mais complicado porque tem o termo que a gente quer, então vamos ver como é que a gente olha pra ele:

∫ S c t τ ∙ n ^   d S = ∫ A 1 + A 2 + A P τ ∙ n ^   d S

A tensão nesse caso é a mesma coisa que pressão, e elas tem a mesma unidade. Múltiplicada pela área temos unidade de força!

∫ A 1 τ ∙ n ^   d S = P . A 1 = - 249,6   N

∫ A 2 τ ∙ n ^   d S = P . A 2 = 62,4   N

∫ A P τ ∙ n ^   d S = F x

Passo 5

Juntando tudo temos que:

- 24,18 + 96,75 =   - 2 49,6 + 62,4 + F x

Finalmente:

F x =   259,77   N  

Lembrando que o sinal é só questão de orientação das superfícies, se tivesse dado negativa nossa resposta a gente poderia responder em módulo

Resposta

F x =   259,77   N  

Exercício Resolvido #7

Hauke, G. (2008), An Introduction to Fluid Mechanics and Transport Phenomena, 1st edition, Springer, Berlim, Chapter 6. (Adaptado)

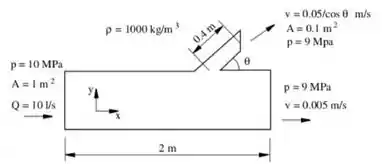
Na tubulação da figura corre um fluido imcompressível. Considerando a gravidade, determine a força que o fluido exerce na tubulação.

Passo 1

Bom, pra essa questão vai ser melhor se a gente ver o equacionamento antes de começar a resolver. Com ele a gente vai vendo o que podemos simplificar e como vamos resolver cada coisa!

Como o problema está pedindo pra gente a força que o fluido faz no tubo, já é um indicativo de que vamos usar a equação da conservação da quantidade de movimento!

d d t ∫ V c ( t ) ρ v   d V + ∫ S c ( t ) ρ v v - v ∞ ∙ n ^   d S =   ∫ S c ( t ) τ ∙ n ^   d S + ∫ V c ( t ) ρ f m   d V

Passo 2

Vamos então ver o que que a gente pode cortar dai!

A gente vai considerar estado estacionário, porque o fluxo de líquido é contínuo, então não tem variação ao longo do tempo. Então, esse primeiro termo vai embora = 0 !

Fluido incompressível, então ρ = c o n s t a n t e .

v ∞ = 0 pois não tem nenhum fluido externo fazendo arraste de espécie.

E vamos considerar f m = g , pois o problema pede para considerar a ação da gravidade.

Nosso balanço ficou então:

∫ S c t ρ v v ∙ n ^   d S =   ∫ S c t τ ∙ n ^   d S + ∫ V c ( t ) ρ f m   d V

Passo 3

Vamos agora definir nossa geometria!

Nosso volume de controle vai ser o volume da tubulação princiál mais o volume do canalzinho que tá saindo dali!

V C = 1   x   2 + 0,4   x   0,1 = 2,04   m ³

As nossas superfícies de controle vão ser as 3 dadas, aonde tem fluido atravessando:

A 1 = A 2 =   1   m ²

A 3 = 0,1   m ²

Passo 4

Vamos resolver cada termo então:

  ∫ S c t ρ v v ∙ n ^   d S = ∫ A 1 + A 2 + A 3 ρ v v ∙ n ^   d S =   ρ V 1 2 A 1 + ρ V 2 2 A 2 + ρ V 3 2 A 3

Pra encontrar as velocidades:

Q = A   x   V

V 1 = V 2 = 10   m / s

V 3 = 0,05 / c o s θ

Como o fluido flui em direções opostas através de A 1 e A 2 :

∫ A 1 + A 2 + A 3 ρ v v ∙ n ^   d S = 0,25   c o s ² θ   N

Olhando agora pro outro termo:

∫ S c t τ ∙ n ^   d S = ∫ A 1 + A 2 + A P τ ∙ n ^   d S

A tensão nesse caso é a mesma coisa que pressão, e elas tem a mesma unidade. Múltiplicada pela área temos unidade de força!

∫ A 1 τ ∙ n ^   d S = P . A 1 = - 249,6   N

∫ A 2 τ ∙ n ^   d S = P . A 2 = 62,4   N

∫ A P τ ∙ n ^   d S = F x

Passo 5

Juntando tudo temos que:

- 24,18 + 96,75 =   - 249,6 + 62,4 + F x

Finalmente:

F x =   259,77   N  

Lembrando que o sinal é só questão de orientação das superfícies, se tivesse dado negativa nossa resposta a gente poderia responder em módulo

Resposta

F x =   259,77   N  

Exercício Resolvido #8

Lista de Exercícios – Transferência de Massa – Prof. Luiz Fernando – UFRJ – 2018

A reação irreversível A   → k 1   B ocorre em um reator de alimentação contínua. As taxas de entrada e saída são 5   m ³ / h , com concentração C A i = 0,18   k m o l / m ³ . A reação é de primeira ordem, com k 1 = 8,5 m ³ / h . Inicialmente o tanque contém 5,6   m ³ de solvente B e nenhum A. Calcule a concentração de saída de soluto após 1 hora.

Passo 1

Bom, vamos então ver aquele passo a passo!

  1. Definir a geometria do problema: Volume de Controle e Superfície de Controle
  2. Montar o equacionamento do problema
  3. Fazer simplificações baseadas nas considerações que o problema te der
  4. Analisar a expressão termo a termo, usando essas simplificações
  5. Juntar tudo e resolver!

Passo 2

Vamos então definir a geometria do nosso problema!

O volume de controle vai ser então o volume que foi dado pelo problema.

V C = 5,6   m ³

A superfície de controle a gente não tem então vamos usar a relação entre a velocidade, vazão e área!

Passo 3

Vamos montar o balanço de massa então:

d d t ∫ V c A ( t ) C A d V + ∫ S c A ( t ) C A v - v c ∙ n ^   d S = - ∫ S c A t C A v A - v ∙ n ^   d S + ∫ V c A ( t ) r A ˙   d V

Como no nosso caso não está acontecendo transporte de espécie por difusão (consideramos mistura perfeita, a velocidade dos componentes é igual à do fluido) temos que:

d d t ∫ V c ( t ) ρ   d V + ∫ S c ( t ) ρ v - v ∞ ∙ n ^ d S = ∫ V c A ( t ) r A ˙   d V

Outra simplificação que podemos considerar também é a densidade constante. Bora então resolver cada um desses termos!

Passo 4

Resolvendo o primeiro termo:

d d t ∫ V c ( t ) C A   d V = V C d C A d t = 5,6 d C A d t

Pra resolver o segundo termo, consideramos v ∞ = 0 , já que não tem nenhum fluido externo fazendo arraste de matéria, quem está escoando é o próprio fluido do tanque. Sendo assim:

∫ S c ( t ) C A v - v ∞ ∙ n ^ d S = C A v S C = C A E Q E - C A S Q S = 5 ( 0,18 - C A S )

Repara que você tem que considerar o que entra menos o que sai!

Agora o último termo:

∫ V c A ( t ) r A ˙   d V = - 8,5   x   5,6   x   C A =   - 47,6   C A

Como A é reagente e está sumindo a gente coloca esse sinal de menos ai!

Passo 5

Juntando tudo temos que:

5,6 d C A d t + 5 0,18 - C A = - 47,6 C A

d C A d t = - 7,6 C A + 0,16

Separando as variáveis:

∫ 0 C A S d C A ( - 7,6 C A + 0,16 ) = ∫ 0 t d t

ln ⁡ - 7,6 C A + 0,16 0,16 = - 7,6 t

Quando t = 1 :

C A S = 0,0 2   k m o l / m ³

Resposta

C A S = 0,0 2   k m o l / m ³