Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 10

A água escoa por um conduto que possui dois ramais em derivação. O diâmetro do conduto principal é 15   c m e os das derivações são 2,5   c m e 5   c m , respectivamente. O perfil das velocidades no conduto principal é dado por: v = v m á x 1 1 - r R 1 2 e nas derivações por: v = v m á x 2,3 1 - r R 2,3 1 / 7 . Se v m á x 1 = 0,02   m / s e v m á x 2 = 0,13   m / s , determinar a velocidade média no tubo de 5   c m de diâmetro. R 1 = r a i o   d a   s e ç ã o   A 1

Passo 1

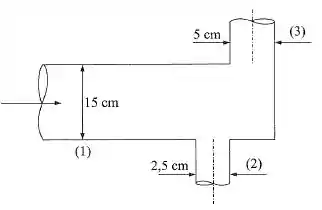
Vamos comigo entender direito esse enunciado! Temos essa situação:

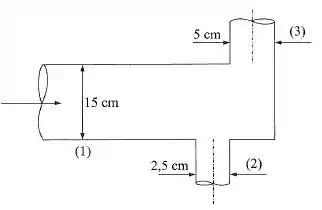
O perfil de velocidade que passa pelo tubo principal, que é o que tem esse ponto (1) é :

v = v m á x 1 1 - r R 1 2

No exercício 3.1   a gente viu esse mesmo perfil de velocidade e lá a gente provou que:

v 1 = v m á x 1 2

E dos tubos (1) e (2) é:

v = v m á x 2,3 1 - r R 2,3 1 / 7

Esse perfil de velocidade já apareceu pra a gente também, com a seguinte relação!

v 2 = 49 60 v m á x 2

Passo 2

Portanto, temos que:

v 1 = 0,02 2 = 0,01   m / s

E:

v 2 = 49 60 × 0,13 = 0,106   m / s

Aplicando a equação da continuidade, podemos encontrar v 3 que é o que queremos, logo:

Q 1 = Q 2 + Q 3

v 1 A 1 = v 2 A 2 + v 3 A 3

Portanto:

v 3 = v 1 A 1 - v 2 A 2 A 3

Substituindo os valores conhecidos e resolvendo, temos que:

v 3 = 0,01 π 0,15 2 4 - 0,106 π 0,025 2 4 π 0,05 2 4

v 3 = 0,064   m / s

Resposta

v 3 = 0,064   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um reservatório contém um gás e tem uma válvula que controla a sua saída de forma que a pressão interna seja reduzida segundo a lei: p = p 0 ( 1 - α t 2 ) Sabe-se que durante a descarga a temperatura
Um veículo de massa m 0 = 900k g move-se com uma velocidade de 30m / s em relação a um inercial, sob a ação de uma força constante de 4500N . No instante t = 0 surge um vazamento no tanque de combustí
Uma chapa fina deve passar de forma contínua num banho de tinta contido num reservatório, como mostra a figura. Em regime permanente, o diagrama de velocidades bidimensional v z = f x é tal que, numa
Considere a relação de quantidade de movimento angular na forma: ∑ M O = d d t ∫ s i s t r× V ρd ° V Qual o significado de r nessarelação? Essa relação é válida tanto em mecânica dos sólidos como dos
Para escoamento permanente com baixos números de Reynolds (laminar) através de um tubo longo, a distribuição de velocidades axiais é dada por u = C R 2 - r 2 , em que R é o raio do tubo e r ≤ R . Inte