Exercícios de Vazão e Volume de Controle - Lista de Exercícios Resolvida

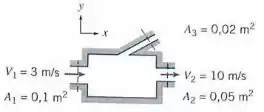
Considere o escoamento incompressível e permanente através do dispositivo mostrado abaixo. Determine o módulo da vazão volumétrica através da abertura e verifique se o fluxo é para fora ou para dentro do dispositivo.

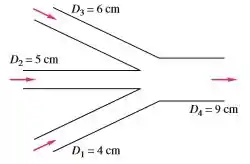
Três tubos fornecem água em regime permanente a para um tubo maior de saída mostrado na figura abaixo. A velocidade e a vazão de saída . Encontre , e se sabemos que aumentando em aumentará em .

A vazão volumétrica de um fluido em escoamento em uma tubulação de um ponto A até um ponto B é . Calcule a vazão mássica do fluido nesse escoamento sabendo que (a) o fluido é a água a 20°C (b) o fluido é etanol a 20°C. (c) O escoamento de qual fluido possui maior vazão mássica? Por que?

Dados: ,

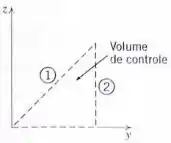
Um campo de velocidade é dado por , onde e . Para o volume de controle triangular de (com profundidade de perpendicular ao diagrama), um elemento de área pode ser representado por e um elemento de área por

Encontre uma expressão para .

Avalie

Encontre uma expressão para

Avalie

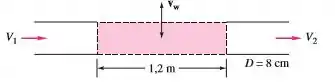
Água escoando por um tubo com de diâmetro entra em uma seção porosa, como mostra a figura abaixo, que permite uma velocidade radial uniforme através das superfícies das paredes por uma distância de . Se a velocidade média na entrada for igual a , determine a velocidade de saída se para fora do tubo ou para dentro do tubo. Qual valor de fará ?

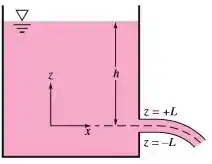
Quando um jato líquido, regido pela gravidade, sai de uma fenda em um tanque, como na figura abaixo, uma aproximação para a distribuição de velocidade na saída é

onde é a profundidade da linha de centro do jato. Próximo à fenda, o jato é horizontal, bidimensional, e de espessura , como mostrado. Encontre uma expressão geral para a vazão volumétrica total que sai da fenda.

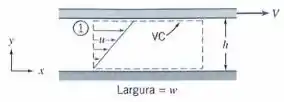
(a) Obtenha expressões para a vazão volumétrica para o fluxo de quantidade de movimento através da secção transversal do volume de controle mostrado no diagrama.

Para o escoamento do item anterior, obtenha uma expressão para o fluxo de energia cinética, , através da seção transversal do volume de controle mostrado.

Uma mangueira de incêndio tem um diâmetro interno de e água está escoando a . O escoamento sai através de um bocal com um diâmetro . Para escoamento permanente, qual deve ser o , em , para haver uma velocidade média de saída de ?

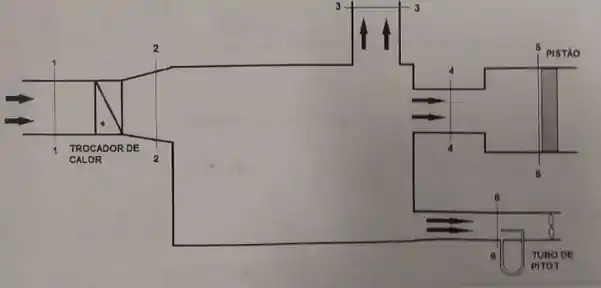
Em um sistema de movimentação de ar apresentado na figura há entrada de ar pela seção 1-1, seguida de um trocador de calor que pode aquecer o ar (condição A) ou não aquecer (condição B). Em seguida o ar é inserido em uma caixa de distribuição de ar podendo escoar para três saídas nas seções 3-3, 4-4 e 6-6. Na seção 5-5 há um pistão que pode movimentar-se ou estar travado em repouso. Na seção 6-6 há um tubo de Pitot posicionado de modo a medir uma velocidade que tem um valor muito próximo ao valor da velocidade média nesta seção transversal, seguido por um ventilador auxiliar.

São dados:

• Na seção 1-1: Vazão em massa , massa específica e área
• Na condição A o trocador de calor aquece o ar e sua massa específica na seção 2-2 é
• As áreas das seções de saída são: e

Pede-se:

1. Para condição A, com o trocador de calor aquecendo o ar, o pistão movendo-se com velocidade constante, e as vazões mássica de saída sendo e , determinar os valores para a vazão em massa , a vazão volumétrica Q3, a velocidade média na seção V3 e a velocidade V5 do pistão na seção 5-5

Em um sistema de movimentação de ar apresentado na figura há entrada de ar pela seção 1-1, seguida de um trocador de calor que pode aquecer o ar (condição A) ou não aquecer (condição B). Em seguida o ar é inserido em uma caixa de distribuição de ar podendo escoar para três saídas nas seções 3-3, 4-4 e 6-6. Na seção 5-5 há um pistão que pode movimentar-se ou estar travado em repouso. Na seção 6-6 há um tubo de Pitot posicionado de modo a medir uma velocidade que tem um valor muito próximo ao valor da velocidade média nesta seção transversal, seguido por um ventilador auxiliar.

São dados:

• Na seção 1-1: Vazão em massa , massa específica e área
• Na condição A o trocador de calor aquece o ar e sua massa específica na seção 2-2 é
• As áreas das seções de saída são: e

Pede-se:

1. Para condição B em que o ar não é aquecido e o pistão está travado, e considerando que as vazões em massa de saída são neste caso, determinar qual a vazão volumétrica Q6 e a velocidade média V6