Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 47
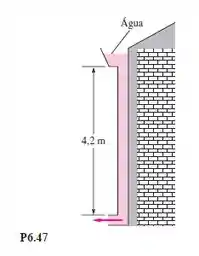
A calha e o tubo liso de drenagem da Figura 6.47 removem água da chuva do telhado de uma edificação. O tubo liso de drenagem tem 7 cm de diâmetro. (a) Quando a calha está cheia, estime a taxa de drenagem. (b) A calha é projetada para uma tempestade súbita de até 127 mm por hora. Nessa condição, qual é a máxima área de telhado que pode ser drenada com sucesso?
Passo 1
Eitaaaa, bora lá resolver mais uma juntos! Pode falar, juntos fica até divertido hehehe.
Bora lançar uma equação de energia ai, bora lá:
Considerando um escoamento incompressível, permanente e que a velocidade lá em cima da calha, quando ela ta cheia, seja , assim:
Sendo , teremos:
Passo 2
Beleza! Chegamos nisso ai, mas e agora? Não temos velocidade, ai não da pra arranjar Reynolds, e, assim, não da pra achar . Mas vamo fazer o seguinte, vamos estimar , porque ai podemos achar uma velocidade estimada e ir corrigindo, assim:
Sabendo que, e que , vamos calcular Reynolds, assim:
Tendo um tubo liso, ou seja, de rugosidade relativa nula, e com nosso número de Reynolds, vamos buscar o novo fator de atrito no Diagrama de Moody. Lá encontraremos que , assim:
Assim, para encontrar a vazão de drenagem, teremos:
Passo 3
Bele, temos um projeto para uma tempestade de . Qual a área máxima do telhado para que possamos ter uma boa funcionalidade da calha?! Vamo lá, é só pegar a vazão de drenagem e dividir pela velocidade da chuva, vê só:
Prontin, acabamos!