Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 43
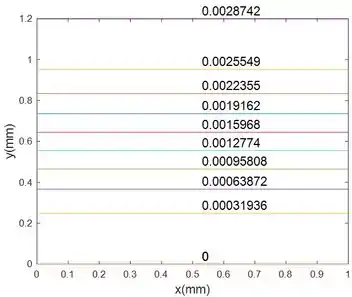
Considere o escoamento em canal da Figura P9-41. O fluido é água a . Para o caso no qual e , faça o gráfico de várias linhas de corrente usando valores igualmente espaçados da função corrente. As linhas de corrente são igualmente espaçadas? Discuta por que sim e por que não.
Passo 1
E aí, pessoal, tudo tranquilo? Prontos para um exercício de função corrente ?
Então vamos ao problema!
O primeiro passo para resolver essa questão é organizar todos os dados que ela deu para a gente. Além disso, como essa questão depende do Problema 9-41, vamos considerar todas as informações presentes nessa questão como dados desse Problema 9-43.
A figura abaixo mostra os dados.
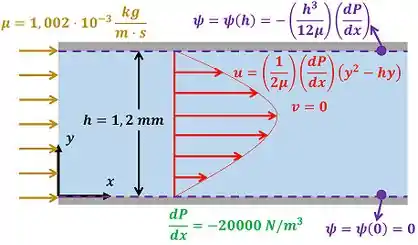
onde é a coordenada vertical dos pontos do escoamento medida da placa inferior. é a componente da velocidade do eixo e é a componente da velocidade no eixo . é a distância entre as placas. é a função corrente do fluido em contato com a placa superior (onde ). é a função corrente do fluido em contato com a placa de baixo (onde ). é a taxa de variação da pressão ao longo do eixo . é a viscosidade da água a .
Passo 2
Agora que organizamos os dados, podemos partir para a resolução da questão.
Esse problema quer que a gente faça um gráfico mostrando as linhas de corrente para vários valores de função corrente . Ou seja, cada linha de corrente tem um valor de função de corrente associado que é constante ao longo de toda a linha de corrente.
Em outras palavras, nós temos que descobrir a posição das linhas de corrente horizontais (nós sabemos que elas são horizontais, porque a componente vertical da velocidade vale zero) para cada valor de . Para visualizar melhor, vamos utilizar a equação de do Problema 9-41.
O que temos que descobrir é para qual valor de , o valor do lado direito da equação fica igual ao valor do lado esquerdo da equação .
Tem outra forma de pensar sobre esse problema que será mais útil para a gente. Para isso, vamos reorganizar a equação acima.
Se considerarmos que uma função de é igual à diferença de termos acima , podemos escrever que:
A outra forma de pensar no problema é: qual valor de faz o polinômio do terceiro grau acima valer zero? Essa forma de ver o problema é igual a todas as outras, porque, quando esse polinômio vale zero, o termo que depende de fica igual ao termo .
Mas não se esqueça que esse valor de tem que estar entre e , porque o escoamento está entre as placas que estão em e .
Mas para quais valores de temos que traçar as linhas de corrente?
Isso é o que descobriremos no próximo passo.
Passo 3
O enunciado não determina para quais valores de ele quer uma linha de corrente. Ele só diz que ele quer que os valores da função corrente para cada linha sejam igualmente espaçados. Isso significa que os valores de para os quais desenharemos uma linha de corrente devem estar em progressão aritmética. Ou seja, a diferença entre o valor de de duas linhas de corrente que estão lado a lado deve ser sempre a mesma.
Para garantir que essa condição seja atendida, vamos definir primeiro o menor valor e o maior valor de que entrarão no gráfico.
O menor valor de que aparecerá no gráfico é o valor de em . Esse valor está presente na figura com os dados.
O maior valor de que aparecerá no gráfico é o valor de em . A fórmula para calcular esse valor está presente na figura com os dados.
Os valores restantes podem ser gerados a partir desses dois limites de ( e ).
Para gerarmos linhas de corrente, precisamos descobrir quanto vale a diferença do valor de de duas linhas de corrente que estão lado a lado.
Para calcular essa diferença, precisamos dividir a diferença total por .
Ou seja, o valor de da corrente de cima é igual ao valor de da corrente de baixo mais . Os valores de para os quais faremos o gráfico das linhas de corrente estão presentes na tabela abaixo.
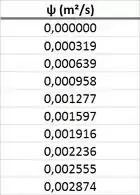
Passo 4
Cada um desses valores de da tabela devem ser substituídos na função . Os valores de das funções de corrente é igual à raiz do polinômio do terceiro grau . Ou seja, precisamos calcular a raiz de para cada da tabela.
Faremos isso com o auxílio de um algoritmo escrito em MATLAB. Segue abaixo o código usado.
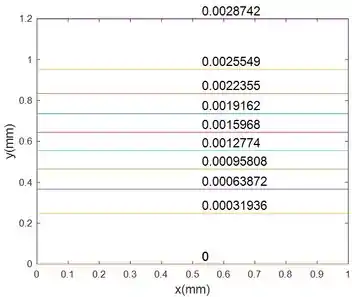
Com esse algoritmo conseguimos gerar o gráfico abaixo. os números sobre as linhas de corrente são os valores de para a linha de corrente.
Passo 5
Vemos na figura que, apesar das linhas de corrente terem valores de igualmente espaçados, suas coordenadas não estão igualmente espaçadas. As linhas de corrente mais ao centro do escoamento estão menos espaçadas (mais distantes) do que as linhas de corrente mais próximas às placas (mais próximas uma da outra).
Isso acontece, porque a vazão por unidade de largura ( onde é a largura das placas) que passa entre duas dessas linha de correntes tem que ser iguais já que:
A figura abaixo mostra essa igualdade de vazão por unidade de largura entre cada linha de corrente.
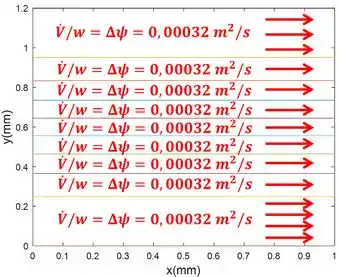
Como a velocidade do fluido cresce conforme nos aproximamos do centro do escoamento, o fluido consegue gerar a mesma vazão por unidade de largura entre espaçamentos menores!
Resposta
