Considere uma parede plana unidimensional com espessura . A superfície em é submetida a condições de convecção caracterizadas por , enquanto a superfície em é submetida a condições de convecção caracterizadas por e . A temperatura inicial na parede é .
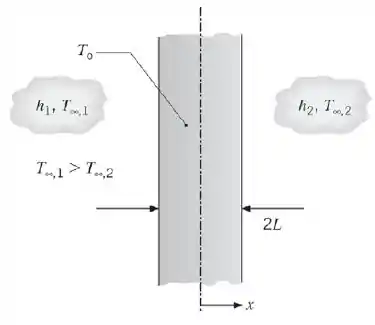
(a) Escreva a equação diferencial e identifique as condições inicial e de contorno que poderiam ser usadas para determinar a distribuição de temperaturas em função da posição e do tempo.
(b) Em coordenadas, esboce as distribuições de temperaturas para a condição inicial, para o regime estacionário e para dois outros instantes de tempo intermediários, para o caso no qual .
(c) Em coordenadas , esboce o fluxo térmico nos planos .
(d) O valor de é agora dobrado, com todas as outras condições sendo idênticas as das partes (a) até (c). Em coordenadas e na mesma escala usada na parte (b), esboce as distribuições de temperaturas para a condição inicial, para o regime estacionário e para dois outros instantes de tempo intermediários. Compare estes esboços com os da parte (b).
(e) Usando o valor dobrado de , esboce o fluxo térmico nos planos e , no mesmo gráfico que você preparou para a parte (c). Compare as duas respostas.
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional, logo a troca de calor só ocorre em uma direção, vamos fazer nosso diagrama pra facilitar nossa vida.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Tendo tudo isso em mente vamos a nossa letra (a), que nos pede as condições de contorno e a nossa equação diferencial. Para isso vamos escrever nossa lei de Fourier (equação ).
Como nossa condução é unidimensional e não há geração de energia, temos:
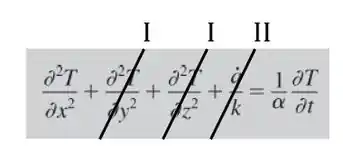
Assim nossa equação fica:
Como quanto nossa temperatura é , em cada superfície será equivalente a temperatura ambiente de cada superfície, ou seja:
Agora pra nossas condições de contorno, nas superfícies o fluxo de calor por condução é igual o fluxo de calor por convecção:
Passo 3
(b) Bem nosso problema nos pede uma representação gráfica da distribuição de temperatura ao longo da superfície, vamos calcular nossa
Integrando duas vezes em função de e temos:
Usando nossas condições de contorno encontramos nosso gráfico que fica assim:
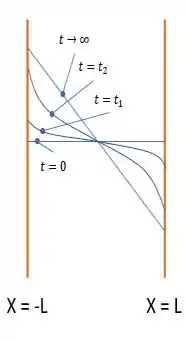
Como não existe geração de calor e , eventualmente nosso gradiente de temperatura vai se tornar constante, e como a temperatura vai decair ao longo do eixo .
No regime permanente nosso fluxo vai ser dado por:
Passo 4
(c) Vamos lá seguindo a lógica do nosso gráfico passado, temos:
Para o instante os nossos fluxos serão idênticos.
Após o passar do tempo os nossos efeitos térmicos chegarão até o centro da parede então o fluxo será constante.
Assim vamos traçar a curva pro centro da parede e pra ambas as superfícies
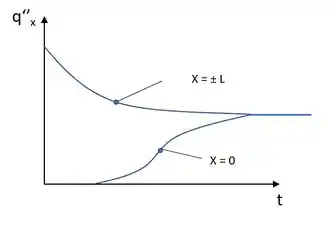
Passo 5
(d) Se dobrarmos nosso coeficiente de convecção a única diferença será pra na superfície pois o fluxo dobra pois.
Daí nossos gráficos ficam:
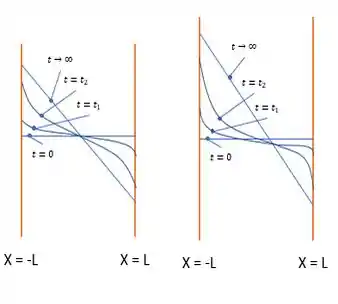
Passo 6
(e) Se dobrarmos nosso coeficiente de convecção a nossas equações de fluxo vão divergir assim temos:
Para o fluxo na superfície será o dobro do valor da superfície .
Depois de um certo tempo os efeitos térmicos vão chegar ao centro da parede e os nossos fluxos serão iguais.
Assim nosso gráfico fica.

Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)