Exercícios de Introdução à Condução - Lista de Exercícios Resolvida

(Adaptada) Considere o problema de condução unidimensional numa parede plana de largura e altura , com uma extremidade isolada e a outra mantida a temperatura igual a .

A parede tem condutividade térmica igual a , e no seu interior passa uma resistência elétrica que gera calor uniformemente a uma taxa de .

Escreva a equação de condução de calor e as condições de contorno apropriadas para essa situação. Em seguida, obtenha a distribuição de temperatura ao longo da parede e desenhe um gráfico (qualitativo) da temperatura x distância para a situação analisada.

Uma placa de cobre com de espessura, de comprimento e de largura encontra-se na posição horizontal. Sua superfície superior é aquecida pelo sol e troca calor com o ar por convecção. A taxa de radiação solar absorvida pela placa é de .

A superfície inferior da placa troca calor por convecção com o ar. Os coeficientes de transferência de calor entre o ar e as superfícies superior e inferior da placa são e , respectivamente.

Determine a temperatura da placa no equilíbrio, sabendo a temperatura do ar é . Suponha que gradientes de temperatura na placa possam ser desprezados.

Uma placa plana de vidro muito fina está inicialmente à temperatura de quando é retirada de um forno. Nesse instante inicial ar é soprado paralelamente à placa produzindo um coeficiente de película para convecção .

Para que o vidro não quebre é necessário limitar o gradiente de temperatura no interior da placa a durante o processo de resfriamento.

Determine qual a temperatura mais baixa que o ar pode ter no início do resfriamento para que o vidro não quebre nesse instante inicial.

Trechos do oleoduto que atravessa o Alasca encontram-se acima do solo e são sustentados por suportes verticais de aço que possuem comprimento de e área de seção transversal de .

Em condições normais de operação, sabe-se que a variação da temperatura ao longo do comprimento do suporte é governada por uma expressão com a forma:

na qual e possuem unidades de e metros, respectivamente. Variações de temperatura na seção transversal do suporte são pequenas.

Determine a temperatura e a taxa de condução de calor na junção suporte-oleoduto e na interface suporte-solo . Explique a diferença entre as taxas de transferência de calor.

Considere condução de calor transiente e uni-dimensional em uma placa plana com propriedades constantes e espessura . A placa, que encontra-se inicialmente na temperatura uniforme , tem suas superfícies em e mantidas nas temperaturas constantes e , respectivamente.

Calor é gerado uniformemente na placa a uma taxa . Para este problema, forneça a formulação matemática.

Uma panela é usada para ferver água. Ela é colocada sobre um fogão, a partir do qual calor é transferido a uma taxa fixa . Há dois estágios no processo.

No Estágio 1, a água é levada de sua temperatura inicial (ambiente) até o ponto de ebulição, quando calor é transferido da panela para a água por convecção natural. Durante esse estágio pode-se admitir um valor constante do coeficiente de transferência de calor , enquanto a temperatura média da água aumenta com o tempo,

No Estágio 2, a água encontra-se em ebulição e a sua temperatura mantém-se em um valor fixo, , enquanto o fornecimento de calor continua.

Considere uma base de panela com espessura e diâmetro , com um sistema de coordenadas no qual e nas superfícies em contato com o fogão e com a água, respectivamente.

Escreva a forma da equação do calor e as condições inicial e de contorno que determinam a variação da temperatura com a posição e o tempo, , na base da panela ao longo do Estágio 1. Expresse o seu resultado em termos dos parâmetros , , , e , assim como das propriedades pertinentes do material da panela.

Durante o Estágio 2 a superfície da panela em contato com a água encontra-se a uma temperatura fixa, . Escreva a forma da equação do calor e as condições de contorno que determinam a distribuição de temperaturas, , na base da panela. Expresse o seu resultado em termos dos parâmetros , , e , assim como das propriedades pertinentes do material da panela.

Um chip, com base quadrada de lado , é montado em um substrato. O substrato comporta-se como um isolante ideal. O chip é resfriado por convecção forçada de ar através da sua superfície superior, que é a única não isolada pelo substrato.

A temperatura do ar é e o coeficiente de transferência de calor é . Sabendo-se que a temperatura da superfície superior do chip não pode exceder , responda qual é a maior potência que pode ser dissipada pelo chip.

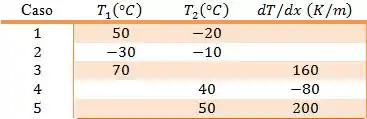
Considere condições de regime estacionário na condução unidimensional em uma parede plana com uma condutividade térmica de e uma espessura , sem geração interna de calor.

Determine o fluxo térmico e a grandeza desconhecida em cada caso e esboce a distribuição de temperaturas, indicando a direção do fluxo térmico.

Um tanque solar de gradiente salino é um corpo raso de água, composto por três camadas distintas de fluidos, que é usado para coletar energia solar.

As camadas externas superior e inferior encontram-se bem misturadas e servem para manter as superfícies superior e inferior da camada intermediária em temperaturas uniformes e , onde . Embora exista movimentação do fluido nas camadas misturadas, tal movimento não está presente na camada central.

Considere condições nas quais a absorção de radiação solar na camada central implique em geração de calor não-uniforme na forma e a distribuição de temperaturas nessa camada seja:

As grandezas , , e são constantes conhecidas que possuem as unidades indicadas e é a condutividade térmica, que também é constante.

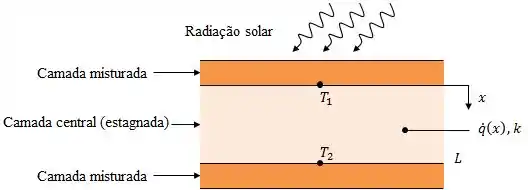
Obtenha expressões para a taxa, por unidade de área, na qual o calor é transferido da camada inferior misturada para a camada central e da camada central para a camada superior misturada.

Determine se as condições do sistema são de regime estacionário ou de regime transiente.

Obtenha uma expressão para a taxa na qual a energia térmica é gerada em toda camada central, por unidade de área superficial.

Em um dado instante de tempo, a distribuição de temperaturas no interior de um corpo homogêneo infinito é dada pela função:

Considerando propriedades constantes e ausência de geração de calor no interior do corpo, determine as regiões nas quais a temperatura varia com o tempo.