64 – Considere um tubo de comprimento , raio interno , raio externo e condutividade térmica por onde passa água refrigerada. A água flui pelo tubo a uma temperatura e o coeficiente de transferência de calor na superfície interna é . Considerando que o tubo é bem isolado na superfície externa, (a) expresse a equação diferencial e as condições de contorno para a condução de calor unidimensional permanente através do tubo e (b) obtenha a relação para a variação da temperatura no tubo resolvendo a equação diferencial.
Passo 1
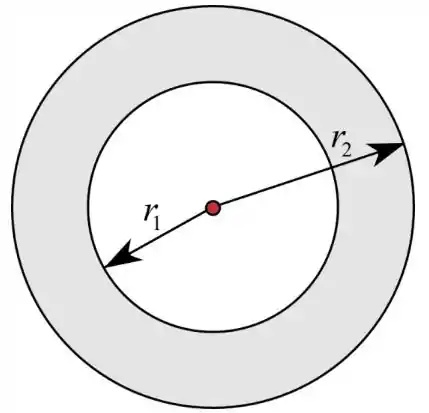
Aqui, está o raio interno do tubo e o raio externo do tubo.
Passo 2
a)
Como a transferência de calor por condução é igual à transferência de calor por convecção.
Portanto,
Aqui, é a condutividade térmica, é o gradiente de temperatura em relação ao raio do tubo, é o coeficiente de transferência de calor, é a temperatura da água e é a temperatura do tubo no raio considerado.
Escreva a equação unidimensional de condução de calor em estado estacionário sem geração interna de calor para as coordenadas cilíndricas,
Integre com relação ao .
Aqui está a constante arbitrária.
Novamente, integre a equação acima em relação a .
Aqui está a constante de integração.
Passo 3
Aplique condições de contorno, pois a superfície externa é isolada, a taxa de transferência de calor será zero a partir da superfície externa.
No ,
Substitua por 0 a equação (2).
Substitua isso na equação (2).
Porque em existe um bom isolamento que leva a transferência de calor para zero.
Portanto, a equação diferencial para a condução de calor unidimensional através do tubo é .
Passo 4
b) Integre a equação (2) em relação a .
Aqui é a constante de integração.
Substitua 0 por .
Na superfície interna , a temperatura é .
Aplique a condição de contorno na superfície interna.
Substituo por , em e para a equação (2).
Substitua na equação (1).
Pela equação (3), (4) e (5).
Portanto, a relação para a variação de temperatura no tubo é
Resposta
a).
E as condições de contorno são:
b)