Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 99
Uma esfera de 0,6 m de diâmetro, pesando 1.780 N, fecha um furo de 0,3 m de diâmetro no fundo do tanque da Figura P2.99. Calcule a força F necessária para desalojar a esfera do furo.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.6 do livro, chamada “Forças sobre superfícies curvas”.
Temos uma esfera de de diâmetro e que pesa , presa num buraco de de diâmetro no fundo de um tanque, como mostra a figura que ilustra a questão. Queremos calcular a força necessária pra tirar a esfera do tanque.
Pra isso, precisaremos calcular a força resultante vertical agindo na esfera, e fazer um balanço de forças usando a força peso.
Então, vamo lá resolver essa questão juntos!
Passo 2
Em primeiro lugar, devemos calcular a força vertical agindo na esfera. Pra entender como vamos fazer isso, vamo olhar essa imagem:
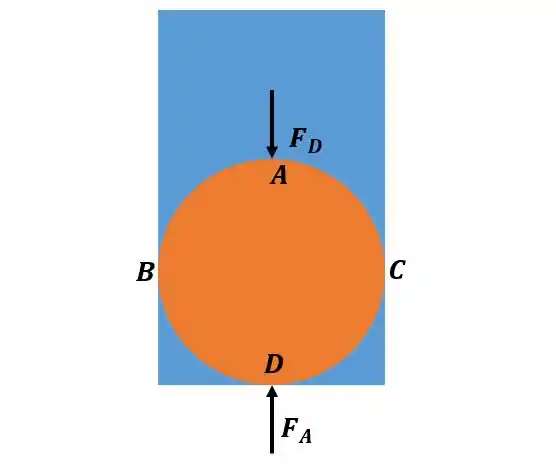
Como mostra o esquema, temos uma força descendente agindo nos pontos da esfera e uma força ascendente agindo nos pontos .
A força vertical resultante vai ser uma menos a outra, mas, se você notar, vai ver que essa força na verdade é o peso da água agindo no volume da própria esfera, pois os volumes menos na verdade é o volume da própria esfera!
Mas olha só, nossa dedução não acabou ainda!
No nosso problema, como a esfera tá tapando o buraco, a nossa força vertical vai ser calculada excluindo o peso da água no buraco, que é calculado a partir da equação:
Sendo: o peso específico, que para água à temperatura ambiente é 9790 ; a área do buraco de raio ; e a altura da superfície livre até o buraco.
Então, podemos calcular nossa força vertical a partir da equação:
Sendo: o volume da esfera de raio .
Substituindo os valores temos, obtemos:
Passo 3
Pra finalizar a questão, vamo calcular a força necessária para tirar a esfera do buraco.
Pra isso, basta a gente subtrair a força do peso da esfera:
Pronto, matamos a questão juntos!
Resposta
A força necessária para desalojar a esfera do furo é