Exercícios de Força em Comportas - Lista de Exercícios Resolvida
Questão 1
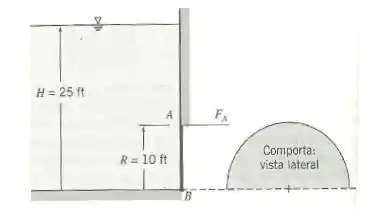
Uma comporta plana semicircular , articulada ao longo de , é suportada pela força horizontal aplicada em . O líquido à esquerda da comporta é água. Calcule a força requerida para o equilíbrio.
Dados:
Questão 2
Um tanque de água tem uma comporta em sua parede vertical com de altura e de largura. O topo da comporta está abaixo da superfície. Qual é a força hidrostática sobre a comporta? E a que distância abaixo da superfície está o centro de pressão da força hidrostática?
Ver solução completaQuestão 3
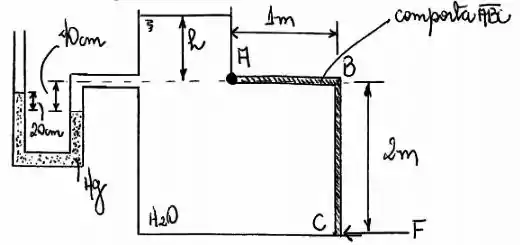
A comporta na Figura abaixo tem de largura, está articulada em e limitada por um limitador em . A água está a . Calcule a força no limitador e as reações em A se a profundidade da água é
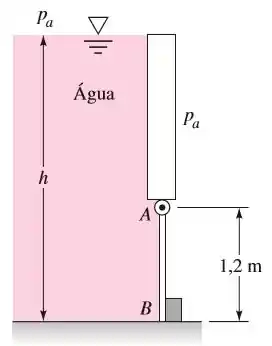
Questão 5
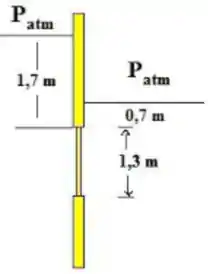
Um portão plano, de espessura uniforme, suporta água a uma certa profundidade, como abaixo. Encontre o peso mínimo que o portão deve ter para que permaneça fechado.
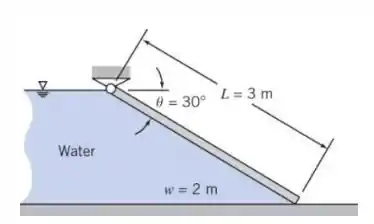
Questão 6
Determine a força e seu ponto de aplicação para a comporta da figura. A substância de trabalho é a água. (Este exercício exige um bom conhecimento da teoria).
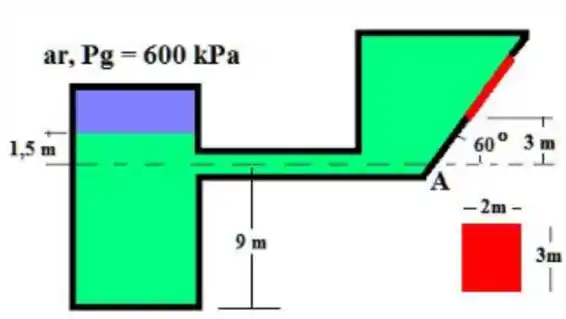
Questão 7
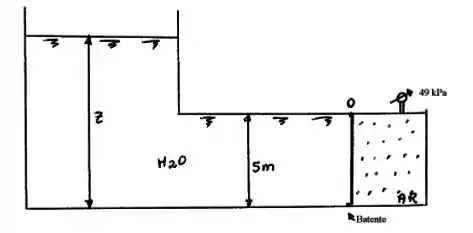
A comporta na Figura abaixo é uma massa homogênea de , de largura, é articulada em e está apoiada sobre um fundo liso em . Todos os fluidos estão a . Para qual profundidade da água a força no ponto será zero?
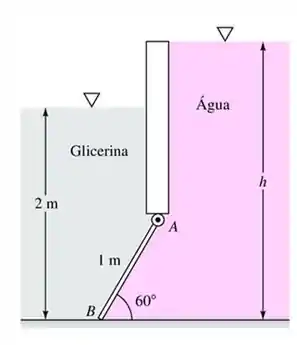
Questão 8
Determinar o mínimo valor de , para o qual a comporta da figura girará em torno do ponto O, se a comporta é retangular de de largura. Dado .