Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 100

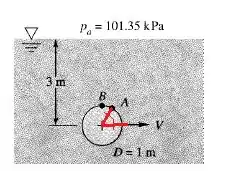
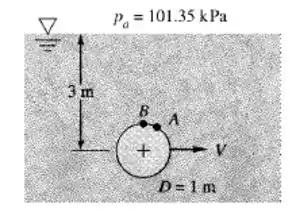
Uma esfera de 1 m de diâmetro está sendo rebocada à velocidade V em água doce a 20°C, como mostra a figura abaixo. Admitindo a teoria não viscosa, com uma superfície livre não distorcida, avalie a velocidade V em m/s na qual a cavitação se inicia sobre a superfície da esfera. Onde a cavitação terá início? Para essa condição, qual será a pressão no ponto A sobre a esfera, a 45° acima da direção do deslocamento?

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Bora lá, vamos obter as propriedades da água a 20°C!!!

ρ = 998   k g / m ³

p v a p o r = 2337   P a

Cavitação acontecerá na menor pressão no nosso ponto de interesse e estudo, que no nosso caso é o ponto B bem no topo do cilindro, em θ = 90 °

Passo 2

Escrevendo nossa equação de Bernoulli, temos que:

p ∞ + ρ 2   U ∞ 2 + ρ g z ∞ = p B + ρ 2   V B 2 + ρ g z B

Onde nossa pressão no ponto ∞ , seria na altura do centro do meu corpo cilíndrico. Temos então que p ∞ = p a t m + ρ g z s u p e r f - z ∞

Vamos substituir nossos valores, beleza? Lembrando que como estamos querendo avaliar a cavitação, a pressão no ponto B deve ser igual a pressão de vapor! Precisamos também lembrar que quando θ = 90 ° , temos que V B = 1,5 U ∞

101350 + 998 9,81 3 + 998 2 U ∞ 2 + 0 = 2337 + 998 2 1,5 U ∞ 2 + 998 9,81 0,5

U ∞ = 14,1   m / s

Essa seria nossa velocidade que causaria cavitação no nosso problema!!

Passo 3

Com a linha de corrente de velocidade conhecida, nós podemos calcular para a pressão no ponto A, ou seja, há 45° ainda dentro da nossa equação de Bernoulli!!!

p A + ρ 2   V s 2 + ρ g z A = p B + ρ 2   V B 2 + ρ g z B

Aí temos que lembrar como é o cálculo de velocidade superficial sobre um corpo curvo como este!!

V s = 3 2 U ∞   s e n θ

Note que Z A

s e n θ = z A R → 0,5 s e n θ = z A

p A + 998 2 3 2 14,1 s e n 45 ° + 998 9,81 0,5   s e n 45 °

= 101350 + 998 9,81 3 + 998 2 14,1 2

p A = 115000   P a

Resposta

U ∞ = 14,1   m / s

p A = 115   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dado o campo de velocidades do escoamento plano de um fluido ideal incompressível: v x = 2 x 2 2 - t - 6 x ⋅ f y , t ⋅ ln ⁡ t v y = - 6 x 2 y2 - t + 2 y 3 ( 2 - t ) Determinar f ( y , t ) para que o e
Seja Ψ = 9 + 6 x - 4 y + 7 x y .Verificar se essa função pode ser a função de corrente de um fluido inompressível.Verificar se o escoamento é irrotacionalDeterminar a velocidade no ponto (0,0)
Um campo de escoamento é representado pela função de corrente ψ = x 5 - 10 x 3 y 2 + 5 x y 4 . Determine o campo de velocidade correspondente. Mostre que este campo de escoamento é irrotacional e obte
A função de corrente de um campo de escoamento é ψ = A x 2 y - B y 2 , em que A = 1 m - 1 . s - 1 , B = 1 3m - 1 . s - 1 e as coordenadas são medidas em metros. Encontre uma expressão para o potencial
A função de corrente de um campo de velocidade é ψ = A x 3 + B ( x y 2 + x 2 - y 2 ) , em que ψ , x , y , A e B são todos adimensionais. Encontre a relação entre A e B para esse escoamento. Encontre o