Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 116

Um fino fio metálico de condutividade térmica k, diâmetro D e comprimento 2L é temperado pela passagem de uma corrente elétrica que induz uma geração de calor volumétrica uniforme, q ˙ . O ar ambiente ao redor do fio está a uma temperatura T ∞ , enquanto suas extremidades em x = ±L também são mantidas a T ∞ . A transferência de calor do fio para o ar é caracterizada por um coeficiente convectivo h. Obtenha expressões para:

  1. A distribuição de temperaturas T(x), em regime estacionário, ao longo do fio.
  2. A temperatura máxima no fio.
  3. A temperatura média no fio.

Passo 1

Vamos que vamos galerinhaa??

Antes de qualquer coisa nós precisamos dar uma olhadinha mais de perto para o balanço de energia em um volume de controle diferencial, ok?

Então, se pegarmos um pedacinho do fio de comprimento d x :

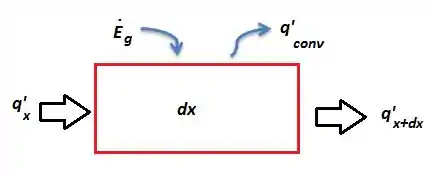
Quando nós fazemos o balanço de energia teremos que o calor sendo adicionado ao volume, q x e E g , referente a geração de energia da corrente, e saindo do volume de controle, q x + d x e q c o n v , Então:

q x + E g = q x + d x + q c o n v

Agora nós precisamos achar cada um dos termos, ok?

A primeira coisa que devemos fazer aqui é escrever a equação de Fourier para a condução que ocorre a uma distância x:

q x = - k A c . d T d x

E para uma distância x + d x :

q x = q x + d q x d x . d x

A transferência de calor por convecção pode ser dada como:

q c o n v = h P T - T ∞ d x

E a última que precisamos achar é a transferência de calor por geração de energia:

E g = q ˙ A c . d x

Agora nós podemos substituir tudo que temos:

q x + q ˙ A c . d x = q ' x + d q ' x d x . d x + h P T - T ∞ d x

q ˙ A c . d x = d q ' x d x . d x + h P T - T ∞ d x

Como o dx está presente em todos os termos:

q ˙ A c = d q ' x d x + h P T - T ∞

E substituindo q ' x :

q ˙ A c = d d x - k A c . d T d x + h P T - T ∞

Se:

A c = π D 2 4

P = π D

Então:

q ˙ π D 2 4 = d d x - k π D 2 4 . d T d x + h π D T - T ∞

q ˙ π D 2 4 = - k π D 2 4 . d 2 T d x 2 + h π D T - T ∞

Reescrevendo:

k D 4 . d 2 T d x 2 - h T - T ∞ + q ˙ D 4 = 0

d 2 T d x 2 - 4 h k D T - T ∞ + q ˙ k = 0

Se nós assumirmos que:

θ = T - T ∞

Então:

d 2 T d x 2 = d 2 θ d x 2

A fórmula fica:

d 2 θ d x 2 - 4 h k D θ + q ˙ k = 0

Quando nós temos uma equação diferencial de segunda ordem com coeficientes constantes a solução é dada pela forma:

θ = C 1 e m x + C 2 e - m x + M m 2

Onde:

m = 4 h k D

M = q ˙ k

Agora nós precisamos aplicar as condições de contorno certo?

Assumindo que no ponto intermediário do fio x = 0 , não haverá variação da temperatura com a posição, ou melhor, d θ d x 0 = 0 .

Derivando:

d θ d x = C 1 m e m x - C 2 m e - m x

No ponto:

d θ d x 0 = C 1 m e 0 - C 2 m e 0 = 0

C 1 = C 2

Como as extremidades também são mantidas a T ∞ , quando x = L teremos θ L = 0 :

θ L = C 1 e m L + C 1 e - m L + M m 2 = 0

C 1 = C 2 = - M m 2 e m L + e - m L

E depois de tanta luta nós vamos substituir nossas constantes na solução:

θ = - M m 2 e m L + e - m L ( e m x + e - m x ) + M m 2

Podemos reorganizar:

θ = - M m 2 cosh ⁡ m x cosh ⁡ m L - 1

Mas o que queremos é a temperatura, certo?

Então vamos substituir θ :

T ( x ) = T ∞ - M m 2 cosh ⁡ m x cosh ⁡ m L - 1

Mas ainda precisamos da letra (b), certo?

Passo 2

Na letra (b) nós queremos a temperatura máxima no fio, certo?

Como a temperatura vai diminuindo até as pontas, de forma que atinja a temperatura ambiente, podemos concluir que a temperatura máxima será com x = 0 .

Substituindo na equação que acabamos de achar:

T ( 0 ) = T ∞ - M m 2 cosh ⁡ 0 cosh ⁡ m L - 1

T ( 0 ) = T ∞ - M m 2 1 cosh ⁡ m L - 1

A letra (b) foi moleza, mas ainda precisamos da (c), certo?

Passo 3

Nela nós queremos a temperatura média no fio!

E como achar?

Simples !! Basta nós usarmos a expressão:

T - = 1 L ∫ 0 L T ∞ - M m 2 cosh ⁡ m x cosh ⁡ m L - 1 . d x

T - = 1 L ∫ 0 L T ∞ . d x - M m 2 ∫ 0 L cosh ⁡ m x cosh ⁡ m L - 1 . d x

T - = 1 L ∫ 0 L T ∞ . d x - M m 2 cosh ⁡ m L ∫ 0 L cosh ⁡ m x . d x + M m 2 ∫ 0 L d x

T - = 1 L T ∞ x - M senh ⁡ m x m 3 cosh ⁡ m L + M x m 2 L 0

Aplicando o intervalo:

T - = 1 L T ∞ L - M m 3 cosh ⁡ m L senh ⁡ m L - senh ⁡ 0 + M L m 2

T - = 1 L T ∞ L - M m 3 tanh ⁡ m L + M L m 2

T - = T ∞ - M L m 3 tanh ⁡ m L + M m 2

E nós finalizamos mais uma em alto estiloo !!

Resposta

  1. T ( x ) = T ∞ - M m 2 cosh ⁡ m x cosh ⁡ m L - 1 ;
  2. T ( 0 ) = T ∞ - M m 2 1 cosh ⁡ m L - 1 ;
  3. T - = T ∞ - M L m 3 tanh ⁡ m L + M m 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Vapor flui a 200 °C em um tubo de ferro fundido ( k = 80W / m ⋅ K ) cujos diâmetros interno e externo são D 1 = 0,20m e D 2 = 0,22m . O tubo é exposto ao ar ambiente a 35 °C. Os coeficientes de transf
Em uma partícula esférica de raio r 1 há geração térmica uniforme a uma taxa q ˙ . A partícula é encapsulada por uma casca esférica com raio externo r 2 , que é resfriada pelo ar ambiente. As condutiv
Uma longa haste cilíndrica, inicialmente a uma temperatura uniforme T i , é subitamente imersa em um grande reservatório de líquido a T ∞T i . Esboce a distribuição de temperaturas no interior da hast
Tipicamente, ar é aquecido em um secador de cabelos ao ser soprado através de um fio enrolado, no qual passa uma corrente elétrica. Energia térmica é gerada pelo aquecimento resistivo elétrico no inte
No exemplo 3.6 foi deduzida uma expressão para o raio crítico do isolante em um tubo cilíndrico isolado. Desenvolva a expressão que seria apropriada para uma esfera isolada.