Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 59

Inicia-se a aplicação de um revestimento plástico em painéis de madeira pela deposição de polímero fundido sobre o painel e o posterior resfriamento da superfície do polímero ao submetê-la a uma corrente de ar a 25°C. Como uma primeira aproximação, o calor de reação associado à solidificação do polímero pode ser desprezado e a interface polímero/madeira pode ser considerada adiabática.

Sendo a espessura do revestimento L = 2 mm e ele estando a uma temperatura inicial de Ti = 200°C, quanto tempo é necessário para a superfície atingir a temperatura segura para o toque de 42°C, se o coeficiente de transferência de calor por convecção for h = 200 W/(m2 · K)? Qual é o valor correspondente da temperatura da interface? A condutividade térmica e a difusividade térmica do plástico são k = 0,25 W/(m · K) e α = 1,20 × 10−7 m2/s, respectivamente.

Passo 1

Vamos analisar o enunciado juntos e entender o que o problema quer de você.

Temos um polímero que deve ser resfriado da temperatura de 200 a 42 ° C em sua superfície. Podemos, então, modelar esse pneu como uma placa plana sofrendo uma transferência de calor transiente com convecção, como demonstra a imagem abaixo:

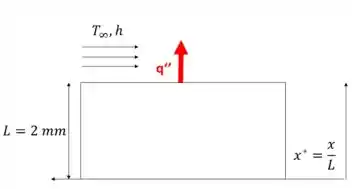
Por isso, se a gente supor tempos muito longos ( F o > 0,2 ) podemos modelar a temperatura adimensional na superfície ( x * = L L = 1 ) a partir da equação:

ϴ S * = T S - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o ) c o s ⁡ ( ζ 1 x * )

Sendo   C 1 e ζ 1 coeficientes que podem ser calculados a partir da Tabela 5.1, F o o adimensional Número de Fourier, T S a temperatura na superfície da placa polimérica, T i a temperatura inicial e T ∞ a temperatura do ar.

Pra resolver o problema, devemos calcular o tempo necessário para a temperatura na superfície atingir 42   ° C .

Depois, devemos calcular a temperatura na interface madeira/polímero ( x * = 0 ):

ϴ 0 * = T 0 - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o )

Sendo T 0 a temperatura em x * = 0 .

Agora, pra gente não se perder, vamos guardar as propriedades que vamos usar nos próximos passos:

T i = 200   ° C ,   T ∞ = 25   ° C   e   T S =   42   ° C L = 2   m m = 0,002   m   k   =   0,25   W m . K ,   α   =   1,20   x 10 - 7 m 2 s h   =   200 W m ²   ·   K

Passo 2

Primeiro, devemos calcular o número de Biot para o problema:

B i =   h L k =   200 W m ²   ·   K 0,002   m   0,25   W m . K =   1,6  

Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de   C 1 e ζ 1 para a parede plana. Como podemos ver na tabela, não temos o valor de B i = 1,6 tabelado. Devemos, então, fazer uma interpolação entre os valores de B i = 1,0 e B i = 2,0 :

B i   = 1,0 →   ζ 1 = 0,8603     C 1 = 1,1191

B i   = 2,0 →   ζ 1 = 1,0769     C 1 = 1,1785

Portanto, interpolando:

B i   = 1,6 →   ζ 1 = 0,9903     C 1 = 1,1547

Vamos deixar o número de Fourier em função do tempo t :

F o = α t L ² =     1,20   x 10 - 7 m 2 s t ( 0,002   m ) ² = 0,03 t

Passo 3

Vamos substituir os valores que encontramos no Passo 2 na primeira equação que deduzimos no Passo 1:

ϴ S * = 1,1547 exp ⁡ - 0,9903 2 0,03 t cos ⁡ 0,9903 1 = 0,6333 exp ⁡ - 0,0294 t

Além disso, devemos lembrar que:

ϴ S * = T S - T ∞ T i - T ∞ =   42   ° C - 25   ° C 200   ° C - 25   ° C = 0,0971

Igualando os dois resultados:

0,6333 exp ⁡ - 0,0294 t =   0,0971   → exp ⁡ - 0,0294 t =   0,1533

Vamos aplicar l n em ambos os lados da equação:

l n ⁡ ( exp ⁡ - 0,0294 t ) =   l n ⁡ ( 0,1533 ) → - 0,0294 t = - 1,8753   → t = 63,79   s

Vamo agora calcular o número de Fourier pra confirmar que nossa suposição de tempos longos tá certa:

F o = 0,03 63,79   s = 1,91 > 0,2

Logo, nossa suposição estava certa.

Passo 4

Agora, vamos finalizar a questão calculando a temperatura na interface polímero/madeira:

T 0 - 25   ° C 200   ° C - 25   ° C = 1,1547 exp ⁡ - 0,9903 2 ( 1,91 ) → T 0 = 56,05   ° C

Fechou? ;)

Resposta

O tempo necessário para a temperatura na superfície atingir 42   ° C   é   t = 63,79   s .

A temperatura na interface polímero/madeira é T 0 = 56,05   ° C .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera sólida de diâmetro igual a D = 100 m m , inicialmente a uma temperatura uniforme de T i = 50 ° C , é colocada em fluido escoando a uma temperatura de T ∞ = 20 ° C . As propriedades da esfer
Considere o duto bem isolado termicamente do Exemplo 5.4, que é subitamente sujeito ao escoamento de um óleo quente. Use uma rotina computacional para a condução transiente em paredes planas para obte
Seja o elemento combustível do Exemplo 5.9, que opera a uma taxa volumétrica de geração unifonne deq, — U)7 W/m3 , até que a taxa de geração mude subitamente para q2 = 2 x 107 W/m3 . Use uma rotina ge
A densidade e o calor específico de um material plástico são conhecidos (p = 950 kg/m3 , cp — 1100 J/(kg-K)), mas a sua condutividade térmica é desconhecida. Para determinar a condutividade térmica, é
Uma placa unidimensional com espessura 2L está inicialmente a uma temperatura uniforme 7). De repente, uma corrente elétrica é passada através da placa, causando um aquecimento volumétrico uniforme j(